La loi des diagrammes de Venn autorise le téléport

[soliris]

Bonjour,

Vous me direz que, comme d'habitude, je viens avec une idée qui ne souffre pas de contradiction. Mais dîtes-moi si j'ai raison.. ou tort.

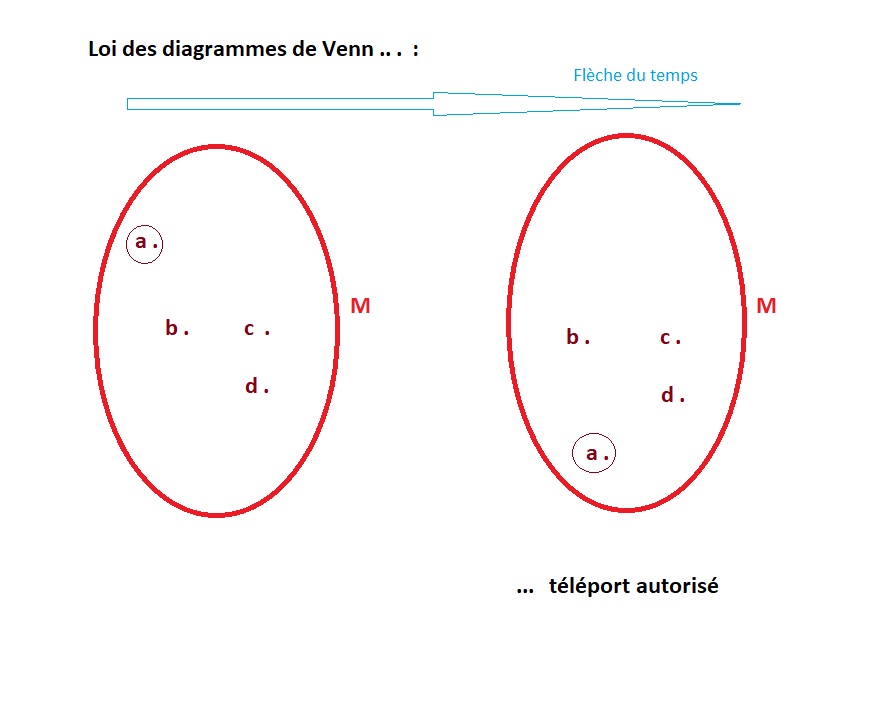
Voici un diagramme de Venn (M) dont les deux représentations montrent le même ensemble différemment à travers le temps; un seul de ses éléments s'est déplacé.



Théoriquement, la structure d'un diagramme de Venn est représentée spatialement par ses limites mais en fait, ce qui "gère" cet espace n'est rien d'autre que l'ensemble des règles qui unissent de façon stricte les éléments qui sont à l'intérieur. L'espace du diagramme n'existe que et uniquement par l'intermédiaire de ces mêmes règles. Donc, quelle que soit la place des éléments, l'espace entre eux est acquis, il est nul sur le plan de l'activité et du déplacement des éléments. L'on pourrait même ajouter que chaque élément n'existe qu' APRES que ses conditions n'aient été respectées.

C'est pourquoi on peut affirmer que le téléport d'un élément, d'un point à un autre, sans considération d'une trajectoire, n'est pas en contradiction avec les règles qui régissent l'ensemble dans lequel il fait partie.
Donc le téléport d'un élément est autorisé dans un diagramme de Venn, ou dans tout autre contexte, par extension, unifié par les mêmes règles et limites.

Alors: Vrai ou faux ?
-----

[Deedee81]

Salut,

Alors: Vrai ou faux ?

Vraux

Bon, c'est juste du grand n'importe quoi, un délire psychiatrique profond.

[Deedee81]

.... et c'est en plus une violation du point 6 de la charte.

Et comme tu connais bien les règles et comme tu fais ta proposition en demandant de répondre juste vrai ou faux, ça signifie que tu l'as fait volontairement. Tu violes la charte en toute connaissance de case.
Je vais donc sanctionner.

Merci,