Bonjour,
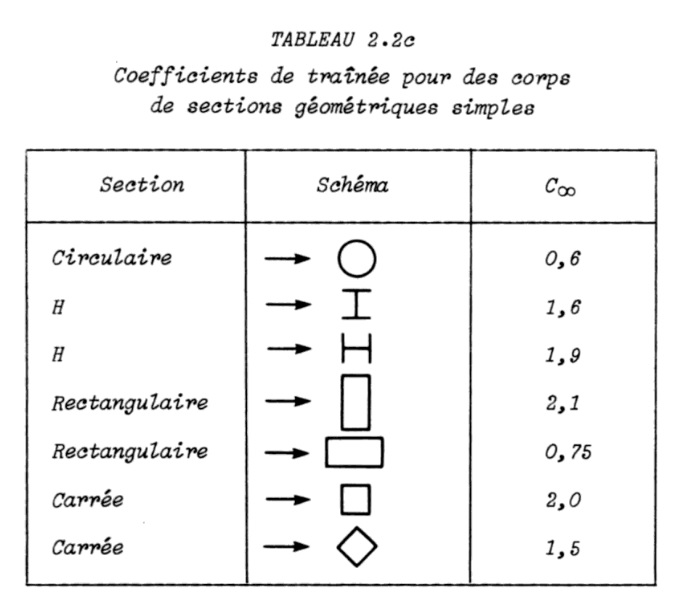
On peut calculer la résistance à l'avancement d'un objet dans l'air : en utilisant la formule F = 1/2 Cx.rho(air).S.V² .
Je voudrai savoir comment s'y prendre si l'objet est immergé dans l'eau, quelles formules appliquer et comment prendre en compte de fameux nombre de Reynolds.
Le coefficient aérodynamique d'une forme donnée est-il toujours valable quand le milieux considéré n'est plus de l'air, mais de l'eau ?
Je cherche à calculer la vitesse de dérive d'un flotteur soumis à la pression du vent sur sa partie émergée, et à la réaction de l'eau liée à sa partie immergée.
Cordialement,
-----





 où:
où: avec {\displaystyle \mu }
avec {\displaystyle \mu } :
: 
 linéaire » (par opposition au {\displaystyle C_{x}}
linéaire » (par opposition au {\displaystyle C_{x}} de la sphère comme longueur caractéristique
de la sphère comme longueur caractéristique et le {\displaystyle C_{x}}
et le {\displaystyle C_{x}} (en référence au diamètre {\displaystyle D}
(en référence au diamètre {\displaystyle D} où :
où : En fait, le problème est plus complexe, et cette estimation de la dépendance en V de la force F ne fait que donner "un ordre d'idée" de la dépendance réelle. La force réelle, trop complexe pour se résumer à une simple puissance de V, peut cependant, d'après les résultats expérimentaux, être bien approchée par une constante de proportionnalité que multiplie
En fait, le problème est plus complexe, et cette estimation de la dépendance en V de la force F ne fait que donner "un ordre d'idée" de la dépendance réelle. La force réelle, trop complexe pour se résumer à une simple puissance de V, peut cependant, d'après les résultats expérimentaux, être bien approchée par une constante de proportionnalité que multiplie