Optique géométrique

[Leol13]

Bonjour,

Je recherche de l'aide pour un exercice d'optique géométrique, matière dans laquelle je suis extrêmement faible, j'ai vraiment du mal à comprendre.

Voici le "speech" initial :

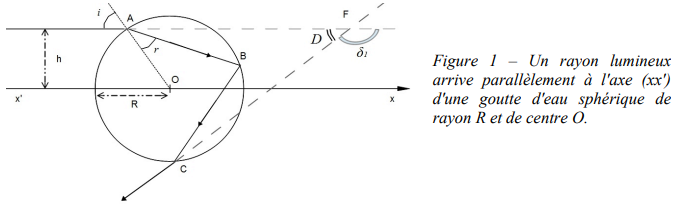
Le cercle de centre O et de rayon R représente une vue en coupe d'une goutte d'eau sphérique. Cette goutte est éclairée par une multitude de rayons solaires arrivant tous parallèlement à la direction (x'x).
Concentrons-nous d'abord sur le rayon lumineux entrant dans la goutte en A, écarté de l'axe d'une distance h.
Ce rayon subit une première réfraction en A, puis une réflexion en B1, puis ressort de la goutte au point C. On supposera dans cet exercice que l'indice de réfraction de l'air vaut na = 1 et que l'indice de l'eau est ne.

Voici le schéma :


Voici les questions :

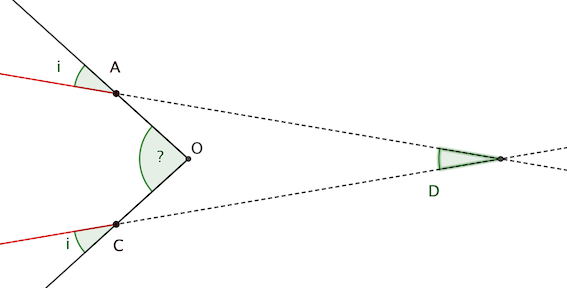
1 . Dans cette question, on cherchera à déterminer l'expression de l'angle d'ouverture D entre le
rayon entrant dans la goutte et le rayon sortant, en fonction de la hauteur h d'entrée du rayon dans la
goutte.
a) Quelle est la relation entre h et l'angle d'incidence i de la lumière au point A.
b) En appliquant la loi de la réfraction, donner l'expression de l'angle r en fonction de la
hauteur d'incidence h, du rayon de la goutte R et de l'indice optique ne de l'eau.
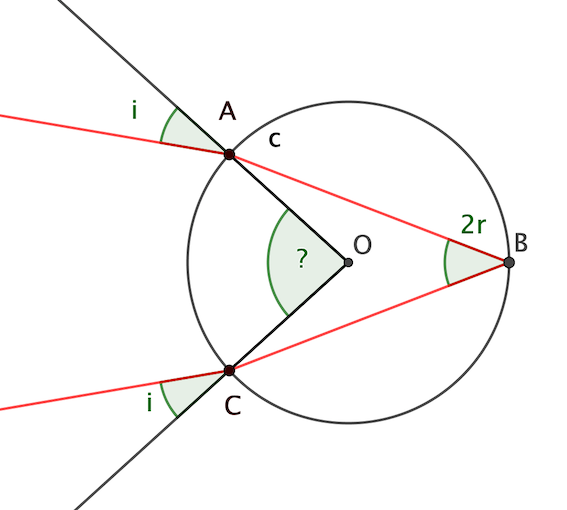
c) Quel est l'angle d'arrivée b du rayon en B? En déduire avec quel angle b' il repart. Faire
apparaître ces angles sur un schéma.
d) On déduira de la même façon l'angle d'incidence c du rayon en C, ainsi que l'angle c' de
sortie de la goutte. Faire apparaître ces angles sur un schéma.
e) Déterminez à présent l'expression de D, exprimez la en fonction de h, R et ne.

Le problème, c'est qu'il y a en tout 8 questions, mais qu'elles sont interdépendantes. Donc je suis bloqué sur tout l'exercice tant que je ne réussi pas la question 1...

Pour le moment, j'ai trouvé :

a) J'ai construit un triangle rectangle avec h et R autour de l'angle i, et je trouve sin(i) = h/R.
b) A partir de sin(i) = h/R, j'applique sur la loi de Descartes n1sin(i)=n2sin(r). J'ai donc trouvé n1(h/R)=n2sin(r) <=> sin(r)=n1/n2(h/R)
c) Je suis parti du principe que la normale de B coupe en O, et créée un triangle OAB isocèle en A et en B, donc l'angle b=l'angle r, et l'angle b'= l'angle b=l'angle r
Sur la d et la e, par contre, je bloque totalement. J'ai tourné et retourné le problème, cherché sur internet, essayé de trouver des exemples, mais je ne vois pas. Je suis franchement une quiche en optique donc ça vient très probablement de moi, mais si quelqu'un veut bien m'aider pour éclaircir ça ce serait super cool.

Merci
-----

[jiherve]

bonsoir
la normale est aussi bissectrice.
JR

[gts2]

Bonjour,

Vous avez a priori compris, il suffit de continuer :
- le passage de B à C est le même que le passage de A à B
- la sortie en C est l'inverse de l'entrée en A

[Leol13]

Bonsoir,

Je vous remercie pour votre réponse.

J'ai tenu compte du fait qu'elle soit bissectrice dans le c), étant donné que l'angle b=l'angle r, et du fait de la normale bissectrice, alors l'angle b'= l'angle b = l'angle r.

Mon problème dans le d) réside dans le fait de trouver l'angle d'incidence c du rayon en C, ainsi que l'angle c'. Ils doivent certainement se trouver de la même façon que l'angle b et b' (à moins que j'ai faux depuis le début, ce qui est une possibilité), mais j'ai du mal à trouver comment vérifier. Je partirai du principe que la normale passe par C et par O, mais je ne trouve pas de triangle pour justifier les angles c et c', comme je l'ai fait précédemment...

J'ai essayé de faire le e) indépendamment du d), mais j'ai vraiment du mal à visualiser comment démontrer D. En cherchant sur internet j'ai cru comprendre que D correspondait à la déviation, j'ai vu pas mal d'exemples qui trouvaient D avec des valeurs comme pi, ou par rapport aux angles i et r, et j'ai du mal à comprendre comment l'exprimer avec h, R et ne.

[A voir en vidéo sur Futura]

[Leol13]

Bonsoir,

Je vous remercie pour votre réponse. Je n'ai vu votre message qu'après avoir envoyé ma réponse à jiherve.
Tout d'abord merci car je ne savais pas si ma direction était la bonne, donc ça me rassure car j'avais l'impression d'avoir des pistes sans justification précise.
Ensuite je pense avoir compris, si le passage de B à C est le même que de A à B, je peux partir du principe que la normale de C passe de C à O, ce qui donne un triangle isocèle en O et en B. A partir de là on a angle c = angle b', (Modification je suis allé trop vite, pas "et par extension = angle c'"), c'est bien ça ?
Et par extension on a sin(c')=n2/n1sin(c) ?

[jiherve]

re
un rayon est toujours normal au cercle qu'il sous tend.
JR

[Leol13]

Re,
Je suis désolé je ne suis pas sûr de comprendre ?

[gts2]

A partir de là on a angle c = angle b' ; Et par extension on a sin(c')=n2/n1sin(c) ?

Oui et comme b'=r, sin(c')=n2/n1sin(r) et donc c'=?

[Leol13]

D'accord je crois que j'ai compris, merci !
Pour a), on a donc sini=(h/R)
Pour b), sinr=(na/ne(h/R))
Pour c), on a b = b' = sinr = (na/ne(h/R))
Pour d), on a d'une part c = b' = arcsin(na/ne(h/R)) d'autre part sin(c')=ne/nasin(r) donc sin(c') = ne/na*(na/ne(h/R)) c'est bien ça ?

A côté de ça j'ai pu réfléchir à la dernière question en reportant graphiquement les résultats, il me semble qu'on peut trouver un triangle rectangle DFC, rectangle en F, avec [FC] = h+R, et dont l'angle C = c'.
J'arrive à trouver sin(D)=(h+R)/[CD], mais j'ai du mal à mettre en relation avec l'angle c', qui m'a l'air nécessaire pour réussir à exprimer D avec h, R et ne.

Est-ce la bonne piste ?

Je vous remercie beaucoup pour l'aide apportée.

[gts2]

Il faut aller jusqu'au bout : sin(c') = ne/na*(na/ne(h/R)) doit donner c'=qqch de très simple.

Pour ce qui est de la déviation, inspirez-vous du dessin ci-dessous :

[Leol13]

Bonjour,

On a donc sin(c') = ne/na*(na/ne(h/R)) <=> sin(c')=h/R <=> c'=arcsin(h/R) <=> c' = i ?

Pour ce qui est de la déviation, en regardant le dessin ce qui me vient c'est que l'angle O = 2i + 2r ?
Mais je ne sais pas vraiment le justifier, en fait je ne trouve pas de méthodologie concrète concernant l'expression de la déviation, il n'y en a pas mention dans mon cours et en cherchant sur internet je ne trouve que quelques résolutions d'exercices, assez différentes à chaque fois desquelles j'ai du mal à tirer quelque chose.

En vous remerciant

[gts2]

Il y a deux méthodes pour trouver la déviation (qui est simplement l'angle entre les rayons incident et émergent) :
- celle du dessin du message #10 : trouver la relation entre l'angle de déviation et l'angle ?, c'est juste de la lecture de dessin, puis trouver l'angle ? c'est de la géométrie.
- ou alors (en numérotant les différentes trajets dans l'ordre) dire que la déviation 1-4, c'est la déviation 1-2 + celle 2-3 + celle 3-4

[Leol13]

Bonjour,

Je vous remercie pour votre explication. Cependant, je ne comprends pas la relation qui les lie, je crois avoir compris la seconde méthode mais pas la première.

En prenant la deuxième méthode.
Si par exemple je prends la déviation qui se passe à l'angle A, je dois donc trouver l'angle qu'il aurait dû avoir s'il n'avait pas été dévié càd DA = i-r ?
Pour B, pareil, c'est l'angle entre le faisceau dévié et le faisceau qui aurait dû exister s'il n'était pas dévié ? (lui je ne vois pas par contre)
Et ensuite faire la somme de ces angles, c'est bien ça ?

Par contre pour la première méthode, je ne suis pas sûr de comprendre comment appliquer ça désolé

[gts2]

Pour la première méthode, je ne garde dans le dessin que la partie utile :


Pour la déviation en B, tracer le prolongement de AB pour voir le rayon non dévié.

[Leol13]

Donc ça nous fait D = pi +2i - 4r de ce que j'ai compris, c'est bien ça ?

Par contre je suis désolé je ne comprends pas la méthode graphique...

[gts2]

Le ? est 4r (angle au centre double de l'angle inscrit correspondant 2r).

Si on part de cet angle de 4r et qu'on le diminue en A de i (passage du trait noir au trait rouge) et idem en C, on a 4r-2i=D.

La différence entre les deux résultats vient du fait qu'avec cette méthode géométrique on ne tient pas compte du fait que le rayon rouge en A va vers la droite alors que celui en C vers la gauche, il faut donc prendre le supplémentaire ce qui donne bien pi-(4r-2i)=pi+2i-4r.