cinématique du point : toboggan

[lcisse2]

Bonjour , j'ai une question et je ne sais pas si c'est bien ce que je dois faire

le 0 est l'angle téta car je n'arrive pas à faire le symbole sur pc

Merci d'avance pour vos réponses
-----

[lcisse2]

du coup j'ai continué , mais je ne sais tjr pas si c'est bon ce que je fais Capture2.PNG Capture3.PNG

[gts2]

Bonjour,

Le texte dit : "après qu'il a quitté le toboggan" donc RT n'existe pas.
D'autre part la force de frottement est -kv pas -K.
Et enfin la vitesse projetée sur les axes x et z s'exprime simplement en fonction de x(t) et z(t).

[lcisse2]

Bonjour , le vecteur v est diriger suivant u téta ? ça veut dire que on peut remplacer v par cos thêta sur x et sin thêta sur z

[A voir en vidéo sur Futura]

[gts2]

Encore plus simple, et respectant le texte qui vous demande "les équations différentielles vérifiées par x(t), z(t)" : d'où

[lcisse2]

c'est la dériver de x(t) et z(t) par rapport au temp mais c'est juste ça que je dois écrire ?

[lcisse2]

ou x(t) = RT sin théta et Z(t) = RT cos théta que je dérive

[gts2]

x'(t) et z'(t) c'est quand même plus en lien avec la question "les équations différentielles vérifiées par x(t), z(t)", non ?

[lcisse2]

j'ai l'impression que il me demande x''(t) et z''(t) mais merci beaucoup je sais ce que je dois faire , par contre j'ai pas compris cette histoire de il quitte le toboggan ça veut dire que le point m a dépassser le point B par la gauche et il est dans le vide ?

[gts2]

j'ai l'impression que il me demande x''(t) et z''(t)

C'est bien cela.

Par contre j'ai pas compris cette histoire de il quitte le toboggan ça veut dire que le point M a dépassé le point B par la gauche et il est dans le vide ?

Oui, c'est comme cela que je traduis et le toboggan est le quart de cercle à droite, mais au vu de l'énoncé il doit y avoir une question/présentation avant qui explique le schéma.

[lcisse2]

Est-ce que ça donne ça ? pck si c'est juste je ne sais pas comment répondre la 3 pour x'

[gts2]

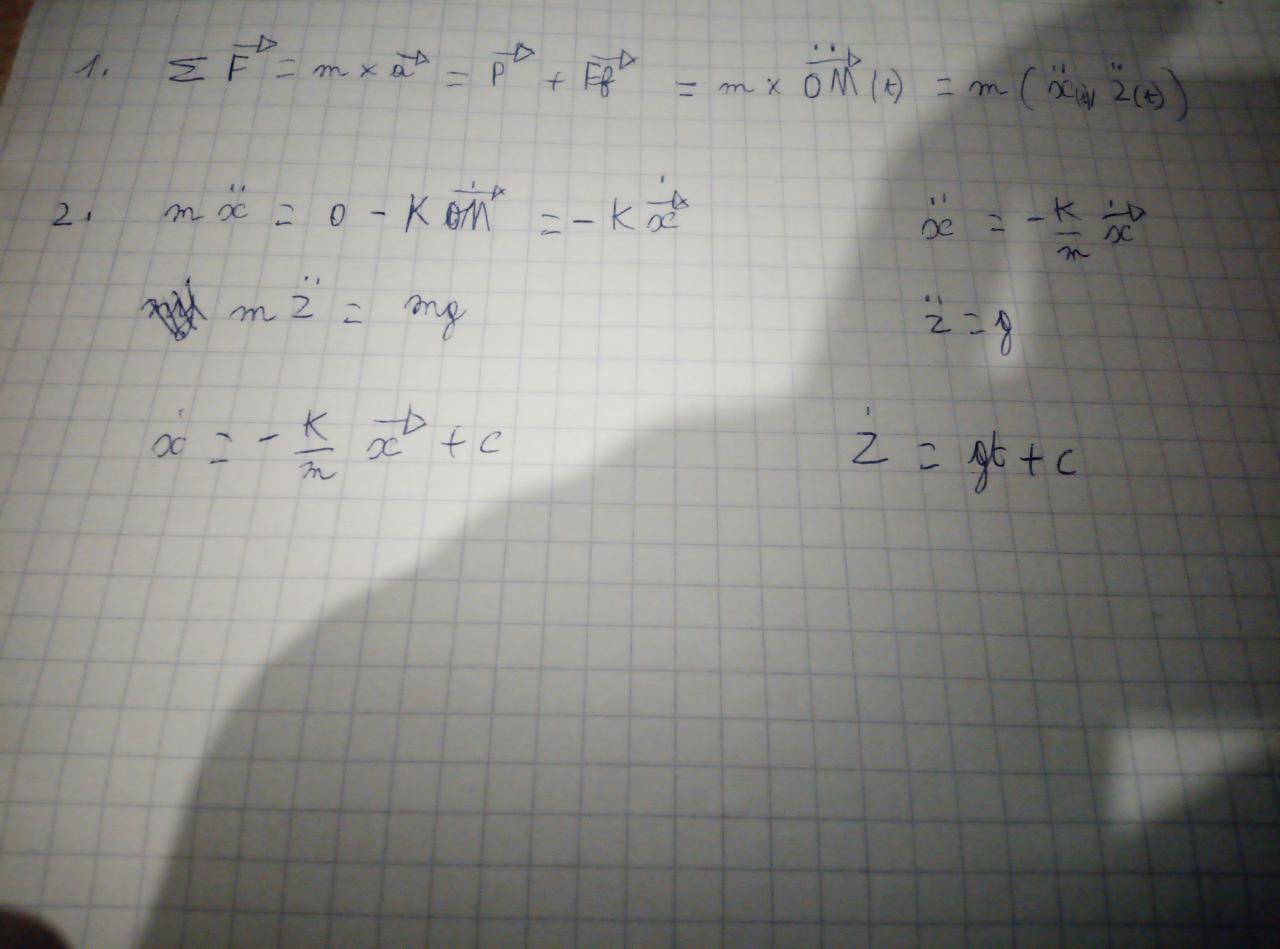
OK pour l'équation en x et l'intégration correspondante.
Par contre pour celle en z où est passée la composante selon z de la vitesse ?

Et cela a des conséquences sur la question 3.

[lcisse2]

Ah oui je l'ai oublié, mais les forces de frottement ne sont pas censé être positive sur x ? Puisque c'est dans le sens inverse de la vitesse et l'axe des x est dirigé vers la droite, et pour x' on à pas de t dans l'équation comment je peux répondre à la 3 ?

[gts2]

les forces de frottement ne sont pas censé être positive sur x ? Puisque c'est dans le sens inverse de la vitesse et l'axe des x est dirigé vers la droite

Oui, où est le problème ?

et pour x' on à pas de t dans l'équation comment je peux répondre à la 3 ?

L'équation en x(t) est une équation connue, dont on ne connait la solution, il est pas nécessaire de la calculer, expliciter ..., la forme suffit pour répondre.

[lcisse2]

j'avais mis un - devant le K pour x'


Je suis désolé je n'ai pas compris ce que vous voulez dire, d'habitude en classe pour ce genre de question on remplace t par une valeur très grande et on regarde comment tend l'équation.

quand t =0 x'(t) = 0 la constante de notre intégration = (k/m)*x , je ne sais pas ce que il faut faire après

[gts2]

j'avais mis un - devant le K pour x'

Il y a bien un - devant K : la force de frottement est bien -k v, et -Kx' est bien positif puisque x' est négatif.

Je suis désolé je n'ai pas compris ce que vous voulez dire, d'habitude en classe pour ce genre de question on remplace t par une valeur très grande et on regarde comment tend l'équation.

Quand on a une fonction, oui, mais là vous avez une équation différentielle.

quand t =0 x'(t) = 0

Tout dépend où vous mettez votre t=0 ...

la constante de notre intégration = (k/m)*x

Ceci n'est pas la constante d'intégration mais une primitive de k/m x'.
Les conditions initiales doivent être dans es questions précédentes.

je ne sais pas ce que il faut faire après

Vous avez une équation du type x'=-k x, quelle type de solution en x(t) ? que peut-on dire de x(t) pour t très grand ? et donc que dire de x'(t) pour t très grand ?

Ceci étant, tout peut se faire à partir de l'équation de départ en z" / x".

[lcisse2]

la solution est K1e(-Kt/m) ? y'a pas de condition initial mais j'imagine que x'(0)=0

[gts2]

Il y a peu de chance qu'en sortant du toboggan la vitesse horizontale soit nulle.
Donc la solution est plutôt K2 + K1 e(-Kt/m) mais cela ne change rien, que devient x(t) et donc vx(t) pour t grand ?

[lcisse2]

elle tend vers 0 merci