Theoreme de l'energie cinetique , je coince

[marzzz]

Bonjour
Je bloque depuis longtemps sur une partie du theoreme de l'energie cinétique

En partant de la 2eme loi de newton et en appliquant la notion de travail on arrive à cette formule (ps je ne sais pas mettre une fleche vecteur)

F= ma (F est constant)
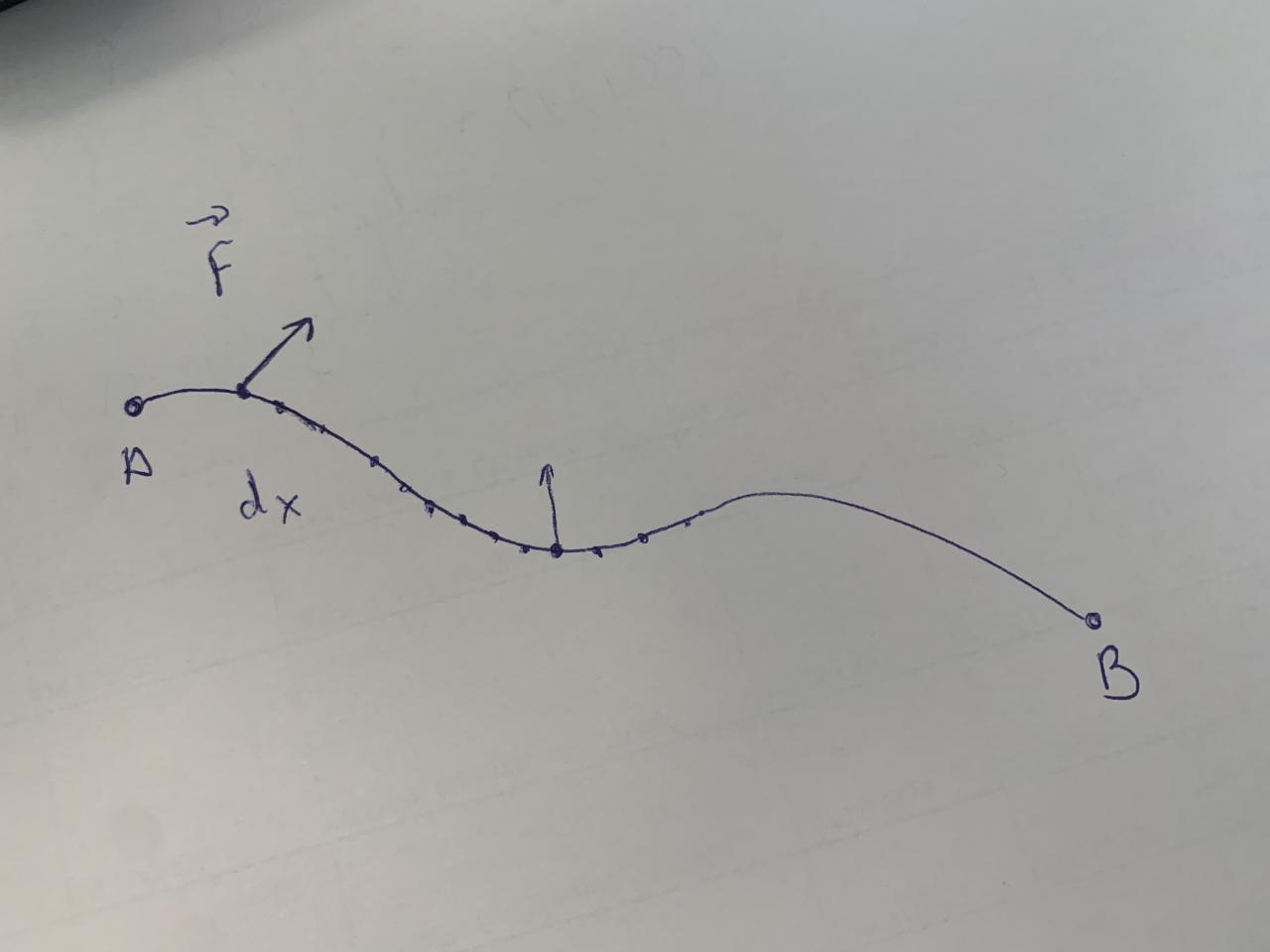
dW= F.dx ( produit scalaire)
dW= mdV/dt.dx
dW= mdV .dx/dt
dW= mdV . V

mon gros problème: comment dV.V devient d(1/2V^2) ?
On utilise un système de chaine de dérivation ?

D'ailleurs a quelle moment le produit scalaire disparait et comment ( il y a en principe le cosinus de l'angle entre le vecteur force et le vecteur dx)

Qui peut m'expliquer
Merci
-----

[sh42]

Bonsoir,

La dérivée de 1/2V^2 est 2/2 V.dV, comme la dérivée de x^2 est 2x.dx.

[marzzz]

ah ok merci
comme quoi j’ai du mal à passer des math à la physique avec l’ecriture differentielle
pour moi d(x^2) = 2x
si effectivement d(x^2) = 2x dx , je comprends mieux

et pour le produit scalaire et son cosinus ?

[Sethy]

Pour la question du cosinus, je dirais fait un dessin de ce que tu calcules et puis essaye de comprendre. Si cela ne va pas, tu nous soumets le dessin et on partira de là.

Pour la partie mathématique, si tu écris avec "d" d'un côté, il faut un "d" de l'autre. d(x^2), c'est quantité infinitésimale et donc cela ne peut valoir qu'une autre quantité infinitésimale.

d/dx (x^2) = (x^2)' = 2x est également légitime puisqu'on prend la dérivé (l'écriture "fractionnaire" d/dx ou ici d/dV équivaut à dériver par rapport à x ou à V).

[A voir en vidéo sur Futura]

[Archi3]

ah ok merci
comme quoi j’ai du mal à passer des math à la physique avec l’ecriture differentielle
pour moi d(x^2) = 2x

parce que tu confonds dérivée et différentielle
la dérivée f'(x) est la limite du quotient de l'accroissement de f sur l'accroissement de x quand celui ci tend vers zéro. Symboliquement on la note parfois df/dx où df est "une petite variation infinitésimale" de f (c'est de la vision des physiciens, les mathématiciens ont une définition rigoureuse et moins vague et intuitive, mais en physique ça reste utile de considérer ça comme une "petite variation"). Par exemple pour calculer la vitesse d'une voiture en km/h, tu peux attendre juste une seconde, ou meme juste un dixième de seconde , et voir la "petite distance "de l'ordre de quelques mètres qu'elle va parcourir. A la limite tu peux faire tendre cette quantité vers zéro et attendre même une nano seconde, une pico seconde et mesurer la distance en nanomètres ou en picomètres qu'elle va parcourir. Ces distances et ces temps sont infinitésimaux mais en divisant l'un par l'autre tu retrouves toujours la même vitesse, par exemple 80 km/h

Dans cette notation, df représente cet accroissement infinitésimal, pas la dérivée. En revanche on a bien df = f'(x) dx. Mais il faut bien mettre le dx pour garder le cote "infinitésimal" car f'(x) a une valeur qui peut etre "grande", qui n'est pas infinitésimal.

Ce n'est pas très rigoureux mathématiquement mais il faut comprendre que tout ce qui commence par "d" est infinitésimal et que si il y a quelque chose qui a un d... dans une équation d'un coté il y a forcément un autre d... de l'autre coté pour maintenir ce coté infinitésimal . La bonne équation était df = f'(x) dx (ou df = (df/dx) dx ce qui est cohérent comme calcul)

[marzzz]

Admettons qu’une force constante s’exerce le long d’un trajet d’un point A et B
le travail total etant la somme des dW , où passe le cosinus inclus dans le produit scalaire ?
Peut on dire que pour un deplacement infinitesimal dx le cosinus =1 car globalement l’angle entre F et dx varie tout le long du trajet ?

[gts2]

Bonjour le cosinus n'est pas de 1, mais on se "moque" du cosinus le long de la courbe : F étant constante :

[Archi3]

Admettons qu’une force constante s’exerce le long d’un trajet d’un point A et B
le travail total etant la somme des dW , où passe le cosinus inclus dans le produit scalaire ?
Peut on dire que pour un deplacement infinitesimal dx le cosinus =1 car globalement l’angle entre F et dx varie tout le long du trajet ?Pièce jointe 478516

le cas physique correspondant est un champ de pesanteur constant (bonne approximation de celui à la surface de la Terre si tu ne bouges pas trop) (à noter que le dessin que tu as mis ne représente pas une force constante !!) . Dans ce cas en posant F = F ez c'est à dire en définissant un axe Oz parallèle à la force (vertical dans le cas d'un champ de pesanteur), le travail vaut F∆z = F (z_B-z_A) (avec un signe - éventuel suivant l'orientation que tu donnes à Oz). Le cosinus est toujours là, il est "caché" dans le fait que ce qui compte ce n'est pas la longueur totale de la courbe ∆l mais juste le "dénivelé" ∆z : si la courbe parcourue est un segment de droite il est facile de voir que ∆z = ∆l cosA où A est l'angle entre la force et le segment parcouru.