Newton versus Gauss un grand écart négligé ?

[Ladrix]

Bonjour à tous.
Je suis nouveau sur ce site et vous excuserez ce message s'il n'est pas dans la bonne rubrique.

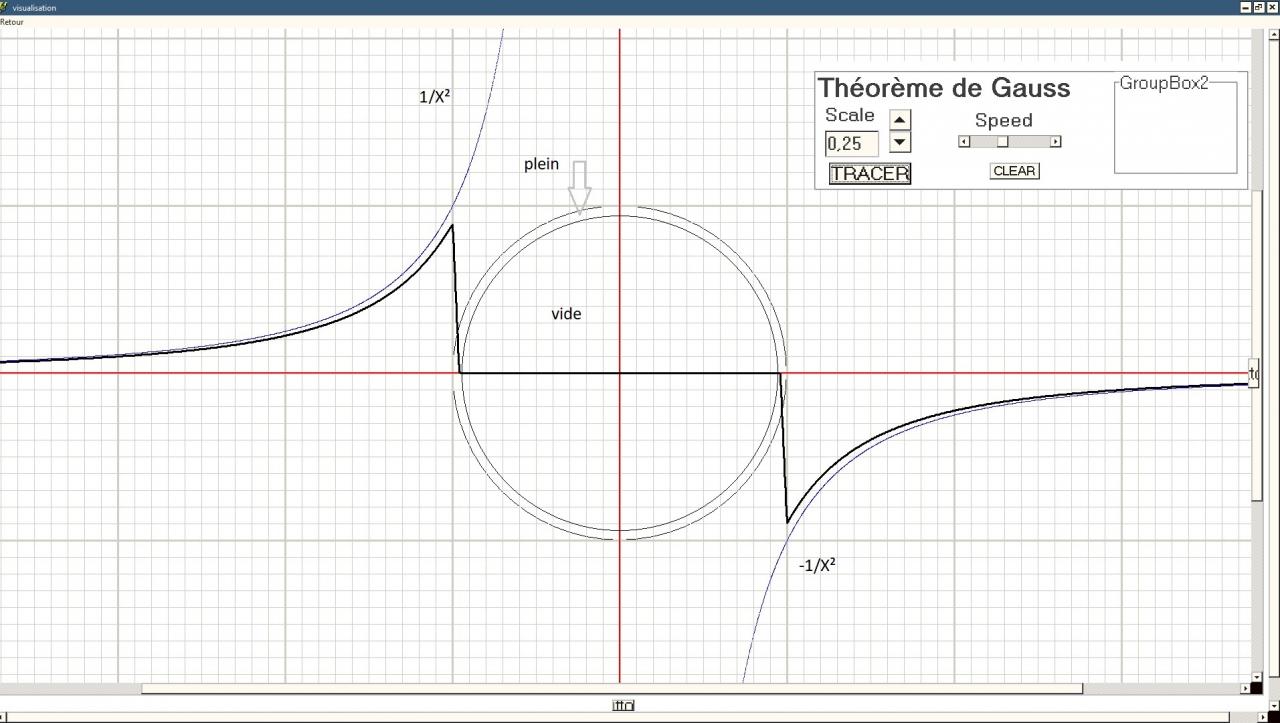
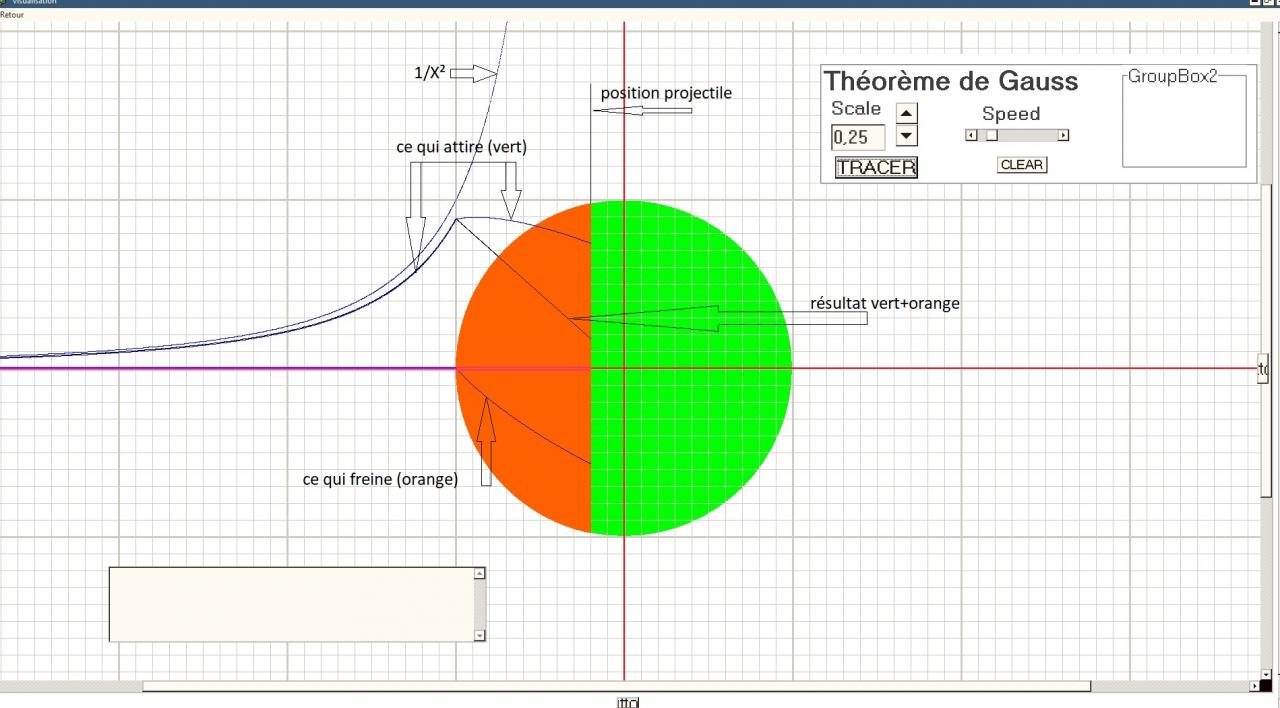
Je travaille depuis une année déjà sur la gravitation vue par Newton. Pour éclairer ma démarche, je fais une simulation de la fonction de Newton par éléments finis.

Un Physicien autorisé, amusé par ma lubie tardive me branche sur le Théorème de la Gravitation de K.F.Gauss.
Mon opinion immédiate fut "La réponse est exacte, l'explication donnée est fausse " mais je suis trop impulsif !!!
Exacte la valeur de F=0 pour d=0, certes. Mais les calculs de Gauss ne m'ont pas convaincu, en fait ses prémices m'ont hérissé le poil. Comme son résultat est exact, je m'attarde sur son travail.

J'ai fait une recherche ici même sur le Théorème de la Gravitation de Gauss et je n'ai trouvé qu'un renvoi fort judicieux sur la page Wikipédia qui en traite dont j'avais déjà pris connaissance. Mes objections restent car le copus calculatoire ne s'appuie pas sur des concepts physiques recevables. Mais ce n'est pas la question qui me fait venir sur ce site.

Ce qui m'amène est la divergence assez conséquente des résultats de notre cher Newton et du respecté Gauss sur la même question physique.

Pour éviter des disgressions intempestives, je précise que la nature de la gravitation n'est pas ici pertinente, qu'on envisage moultes théorie sur la nature du phénomène ne change rien à la question que je me pose.

En effet, en considérant des conditions correspondants à la mécanique classique, les génies précités nous disent :

Newton : la force gravitationelle au centre d'une sphère de rayon et masse indifférente est infinie. c'est le point de vue du Géomètre. (avis personnel)

Gauss : la force gravitationelle au centre d'une sphère de rayon et masse indifférente est nulle. C'est l'avis du Mathématicien.(avis tout aussi personnel)

Considérons que les deux avis sont à évaluer sans a-priori, la valeur scientifique des deux auteurs est non contestable.

Qu'en est-il chez les physiciens de l'écart non négligeable entre les deux calculs tous les deux enseignés aux futurs chercheurs.

Mon but n'est pas de chercher l'erreur, mais de connaître l'opinion des personnes compétentes sur ce sujet.

Je rajoute que Newton lui-même dans ses écrits précise que sa fonction F = G M M' / d² est à considérer comme erronée pour des distances d petites par rapport à la taille des objets en relation.

Mon but est tout a fait raisonnable, trouver la transition entre Newton et Gauss, dans la mesure ou l'un aura raison de (très) loin, et l'autre raison de (très) près.

Merci à tous de me lire et de me soutenir/contester suivant opinions de chacun.

Votre dévoué Ladrix
-----

[Archi3]

je suppose que par théorème de la gravitation de Gauss, tu parles de l'application du théorème de Gauss au champ gravitationnel

https://fr.wikipedia.org/wiki/Théorè...en_gravitation

ce n'est pas différent de la théorie de Newton, mais la loi de Newton s'applique à des objets ponctuels de taille nulle (donc elle n'est plus valable si on pénètre "à l"intérieur" de ces objets, alors que la formulation de Gauss permet de traiter le cas d'objets étendus ayant une certaine taille et une certaine masse volumique. Pour connaitre le champ à l'intérieur de la Terre, il faut utiliser Gauss et on trouve effectivement g=0 au centre (et g croit linéairement avec la distance si on considère que la Terre a une masse volumique homogène). A l'extérieur de la Terre, les deux coïncident. Le théorème de Gauss permet de démontrer que la loi de Newton est exacte à l'extérieur de tout corps de symétrie sphérique, d'où son succès (cependant les écarts à la sphéricité modifient la loi en 1/r^2 et il faut en tenir compte quand on veut des résultats précis à courte distance comme pour prédire le mouvement des satellites par exemple) .

Les deux visions sont approximatives d'ailleurs car à l'échelle des atomes ce n'est ni continu ni discontinu, mais il faudrait appliquer la mécanique quantique à la gravitation et on n'a pas encore de bonne théorie pour ça.

[Ladrix]

Bonjour à tous.

Merci Archi13 pour cette prompte réponse.
La question posée n'est pas celle à laquelle votre message répond. Merci quand même !

Concernant les théories de la nature de la Gravitation, elles sont indifférente dans le cadre de mes travaux et dans la cadre de la question posée. En effet, à mon humble avis, il n'est pas pertinent de théoriser sur la nature de la gravitation, puisqu'a ce jour l'origine du phénomène reste inconnue. (avis personnel)

Il est certain que Newton traite des objets lointains.
Gauss nous dit qu'il traite de l'intérieur des objets.
Certes.

Néanmoins, les règles de Gauss ne sont pas celles de Newton.
C'est ce qui est agaçant.
Gauss nous dit : l'extérieur ne compte pas, n'est pas projeté au centre de l'objet, et nous dit que la masse que je qualifirais de "active" est concentrée au centre, alors que Newton nous dit que au près d'un objet, la règle qu'il avait proposé ne s'applique pas.
L'affirmation de Gauss, "la "force" gravitationelle aurait un sens unique" est assez surprenante. En effet il énonce "De l'intérieur vers l'extérieur y a "force", de l'extérieur vers l'intérieur, y a pas "force". Il st vrai qu'en fait ce serait exact, mais les causes ne sont pas celles énoncées par le Mathématicien.
J'utilise force entre guillements car ce concept est contestable. Sa définition est tautologique mais son usage est généralisé...
Pour étudier le phénomène, j'utilise plutôt une grandeur mesurable : l'accélération gravitationelle.
Celle-ci est définie comme
A= F/M'
on néglige celle de M négligeable pour une m' très petite. Ce qui donne
A = GM/d²
A accélération gravitationelle, G constante dimensionelle, F "force" newtownienne, M la grosse masse active, M' la très petite masse de l'impétrant projectile, d la distance entre les deux objets.

je confirme que la fonction de Gauss à l'intérieur de la cible sphérique (en fait ellipsoide de révolution) serait
A.i= A.r * d
avec
A.i accélération gravitationelle interne, A.r accélération newtownienne mesurée à la surface de la sphère, d distance au centre de la sphère. Je précise "mesurée" car de près la fonction est (relativement) fausse, la mesure est exacte (suivant expérimentateur et matériel dispo)
Je rajouterai qu'on peut croire Gauss qui précise "cette fonction n'est valide que pour une sphère. Mais en fait cette fonction est valide pour les objets de révolution à profil elliptique.

Mais tout ça, ce n'est pas la question posée.

Je répète donc ma question sans l'argumentaire.
Que pensent les Physiciens autorisés (les docteurs et doctorants éventuels) de ces deux lois, celle de Newton et celle de Gauss sur le même phénomène, la gravitation (dans les limites de la physique classique)

Ladrix

Ps
une remarque sur votre réponse :
"

Le théorème de Gauss permet de démontrer que la loi de Newton est exacte à l'extérieur de tout corps de symétrie sphérique"

Ceci n'est pas tout à fait exact. Toute la question est là, la loi de Newton n'est exacte (à epsilon près) que pour de grands éloignements pour une forme quelconque. Réserves de Newton lui-même.

[Archi3]

la loi de Newton (si on raisonne en mécanique classique, pas en relativité) est "complètement" exacte à l'extérieur de tout corps de symétrie sphérique. Pour un corps de symétrie non sphérique, elle est asymptotiquement exacte mais jamais "complètement" exacte, seulement les termes non sphériques décroissent plus vite que en 1/r^2 , et deviennent donc négligeables à grande distance. néanmoins ils ne sont jamais strictement nuls.

Le théorème de Gauss ne dit pas que les masses "à l'extérieur" ne comptent pas. Elles ne comptent pas pour le flux total à travers une surface, mais ça ne veut pas dire qu'elles ne comptent pas localement, elles modifient bien le champ local à l'intérieur. une montagne à la surface de la Terre perturbera bien le champ gravitationnel à l'intérieur. C'est juste le flux (l'intégrale sur une surface) qui n'est pas changé, c'est à dire que les perturbations seront soit dans un sens, soit dans l'autre , mais en s'annulant en moyenne. Ca ne veut pas dire que l'influence est nulle.

Mais quand on est en symétrie radiale, la perturbation ne peut etre que radiale, et donc l'intégrale ne peut être que de la forme ∆g x 4π r^2. Il s'ensuit que si la perturbation totale du flux est nulle, alors le ∆g local doit aussi etre nul. Mais il n'y a qu'en symétrie sphérique stricte que ce résultat est valable (ce n'est bien sûr pas le cas si tu rajoutes une montagne à la surface de la Terre)

[A voir en vidéo sur Futura]

[ArchoZaure]

Bonjour.

Je rajoute que Newton lui-même dans ses écrits précise que sa fonction F = G M M' / d² est à considérer comme erronée pour des distances d petites par rapport à la taille des objets en relation.

Je ne sais pas mais en tous cas Newton a aussi étudié la force de gravitation à l'intérieur d'une sphère.
Il en est ressorti ce qu'on appelle le "shell theorem".
https://en.wikipedia.org/wiki/Shell_theorem

A corollary is that inside a solid sphere of constant density, the gravitational force within the object varies linearly with distance from the center, becoming zero by symmetry at the center of mass. This can be seen as follows: take a point within such a sphere, at a distance r from the center of the sphere. Then you can ignore all of the shells of greater radius, according to the shell theorem (2). But the point can be considered to be external to the remaining sphere of radius r, and according to (1) all of the mass of this sphere can be considered to be concentrated at its centre. The remaining mass m is proportional to r 3 (because it is based on volume). The gravitational force exerted on a body at radius r will be proportional to m / r 2 (the inverse square law), so the overall gravitational effect is proportional to r 3 / r 2 = r , so is linear in r .

These results were important to Newton's analysis of planetary motion; they are not immediately obvious, but they can be proven with calculus. (Gauss's law for gravity offers an alternative way to state the theorem.)

https://en.wikipedia.org/wiki/Shell_theorem

A noter il me semble que mathématiquement, si on x/y=F alors si y tend vers 0 et x tend aussi vers 0 on n'obtient pas nécessairement une valeur F infinie.
Il faudrait demander l'explication à un mathématicien pour confirmer.

[ThM55]

Newton : la force gravitationelle au centre d'une sphère de rayon et masse indifférente est infinie. c'est le point de vue du Géomètre. (avis personnel)

C'est faux, Newton n'a pas écrit cela.

Voir les Principia, Livre 1, section 12, Proposition 73, Théorème 33 (j'utilise la traduction Cohen-Whitman, University of California Press): "a corpuscule placed inside the sphere is attracted by a force poportional to the distance of the corpuscule from the center of the sphere". Donc placé au centre de la sphère, la force s'annule.

La section 12 des Principia est entièrement consacrée à l'attraction gravitationnelle des sphères et Newton montre qu'un corpuscule placé dans une sphère homogène, ou inhomogène à symétrie sphérique, n'est soumise qu'à l'attraction de la partie de la sphère située entre le corpuscule et le centre. C'est une conséquence immédiate du théorème de Gauss, qui lui, est plus général que les théorèmes de Newton.

Il n'y a donc aucune contradiction entre Newton et Gauss.

Mon conseil: au lieu de Wikipedia, qui est une source secondaire pas toujours fiable, lisez les Principia de Newton, c'est totalement accessible. Newton n'aimait pas Descartes. Il maîtrisait parfaitement la méthode cartésienne des coordonnées et de la géométrie analytique mais pour des raisons que je ne connais pas, il la méprisait et trouvait que la méthode descriptive de la géométrie euclidienne lui était supérieure. L'avantage pour le non-mathématicien est que les Principia de Newton demandent peu de connaissances et de pratique de l'algèbre. Presque tout y est démontré par des figures et des preuves descriptives.

[oualos]

Voir les Principia, Livre 1, section 12, Proposition 73, Théorème 33 (j'utilise la traduction Cohen-Whitman, University of California Press): "a corpuscule placed inside the sphere is attracted by a force proportional to the distance of the corpuscule from the center of the sphere". Donc placé au centre de la sphère, la force s'annule.

Cela revient à dire qu'une masse concentrée en son centre n'exerce pas d'attraction sur elle-même...
On ne va pas considérer la force d'attraction exercée sur les électrons très proches du centre de gravité car ce n'est plus du tout de la physique classique pour le coup non ?
Vérifier voire tester si la force de Newton s'exerce à de très petites distances de son centre revient à faire un saut épistémologique en mécanique quantique à mon avis: mais je peux me tromper.
et là avec ce saut la coupure est totale surtout que les forces gravitationnelles jouent très peu en physique quantique comparées aux forces électromagnétiques....

[albanxiii]

Bonjour,

Newton : la force gravitationelle au centre d'une sphère de rayon et masse indifférente est infinie. c'est le point de vue du Géomètre. (avis personnel)

Je ne reviens pas sur le message de thM55, mais vous auriez du vous interroger en écrivant cela.

F = G M M' / d² est à considérer comme erronée pour des distances d petites par rapport à la taille des objets en relation.

Raisonnons un peu sur cette formule... Quand d diminue, que deviennent M et M' ?
Raisonnez sur des boules de bowling, de billard ou de pétanque si vous voulez. Est-ce que vous pouvez avoir d aussi petit que vous voulez ?

[ThM55]

Cela revient à dire qu'une masse concentrée en son centre n'exerce pas d'attraction sur elle-même...
On ne va pas considérer la force d'attraction exercée sur les électrons très proches du centre de gravité car ce n'est plus du tout de la physique classique pour le coup non ?
Vérifier voire tester si la force de Newton s'exerce à de très petites distances de son centre revient à faire un saut épistémologique en mécanique quantique à mon avis: mais je peux me tromper.
et là avec ce saut la coupure est totale surtout que les forces gravitationnelles jouent très peu en physique quantique comparées aux forces électromagnétiques....

Mais que vient faire la mécanique quantique là dedans??? Quand Newton parlait de sphère, il pensait planètes évidemment. Ses "corpuscules" sont de petites quantités de matière assimilable à des points à l'échelle d'une planète ou d'une lune.

[Ladrix]

Bonjour à nouveau.
Note liminaire
les remarques qui suivent sont purement heuristiques.
Fin de note liminaire

@Archi3

la loi de Newton (si on raisonne en mécanique classique, pas en relativité) est "complètement" exacte à l'extérieur de tout corps de symétrie sphérique.

Merci de préciser que A.E. n'est pas invité.
Restons en aux vielles lunes de la mécanique classique, on ne bouge pas : vitesse 0 , on s'occupe que d'une accélération à un point fixe paramètre variant de - inf à +inf en passant par 0
Je suis en contradiction avec cette afirmation d'exactitude de la loi de Newton à l'extérieur d'un objet massique (pléonasme) car le tracé de la courbe de l'accélération gravitationelle tenant compte de la dispersion spatiale de la dite masse infirme la validité de la fonction 1/x² qui est la fonction descriptive des fluxions de la dite courbe.
L'écart à d=r est, semble -t-il de 10 % écart qui tend vers 0 pour les grandes distance mais devient problématique à l'intérieur de la sphère.
Dire que à l'extérieur c'est 1/x² et à l'intérieur ce serait x, me semble inacceptable car il faudrait deux lois de la gravitation suivant l'endroit des deux objet qui sont en interaction gravitationelle.
De plus cette loi ne serait valable que pour la forme sphérique ce qui rabaisserait la loi au rang de recette...
Gauss précise lui aussi cette limitation, donc ce n'est pas une loi.
Je confirme que la courbe de la "force" gravitationelle interne à une sphère est une droite (ce qui m'a beaucoup agacé et même violement contrarié) mais que pour une autre forme de révolution c'est plus voluptueux (dans certains cas)

Le théorème de Gauss ne dit pas que les masses "à l'extérieur" ne comptent pas.

Il dit : "la partie de masse extérieure à une interaction massique nulle vers l'intérieur".(traduction perso)
On en conclu qu'a l'intérieur d'une sphère creuse l'accélération gravitationelle est nulle.
Le plus étonnant c'est que c'est exact, mais pas pour les raisons invoquées par Gauss qui ne sont "que" géométriques. (il faut se rappeler qu'il faisait ça sur une feuille blanche et un stylo, c'est renversant)
Bien sûr, on est dans l'hypothése de "force" gravitationelle venant du centre, une des deux hypothèses avancées par Newton.
Le "flux" partant du centre ne peux pas faire demi tour, donc suivant le principe de la pelure d'oignons, l'intérieur rayonne vers l'extérieur, le "flux" gravitationnel serait donc à sens unique, ce qui est soutenu par rien sinon par l'affirmation que la source du flux est au centre, cad là ou il n'y a plus de matière...Mais il y a la seconde hypothèse de Newton qui propose une source extérieure qui plonge vers le centre (ou il n'y a toujours rien)

ce n'est bien sûr pas le cas si tu rajoutes une montagne à la surface de la Terre

C'est exact car ce n'est plus une sphère...

@ArchoZaure
Merci infiniment pour la page wiki particulièrement performante.
Si je l'avais connue, j'aurais moins réfléchi et je ne viendrai pas vous embêter avec mes questions...
Mais je ferai la même remarque que pour le théorème de Gauss, le traitement est géométrique et la question causale est éliminée.
Pour la limite F=0 elle ne nécessite pas de corpus mathématique au delà de la somme des vecteurs qui est nulle au centre d'une sphère.
La question c'est avant d'être au centre et surtout quelle est la cause physique de cette nullité.

@ThM55

a corpuscule placed inside the sphere is attracted by a force poportional to the distance of the corpuscule from the center of the sphere".

Je n'ai pas (encore) les Principia.
Je ne doute pas de la citation. Donc Gauss n'aurait aucun mérite avec son théorème?
Je suis étonné quand même que les Principia découleraient sur ce point du théorème de Gauss...

@Oualos

Cela revient à dire qu'une masse concentrée en son centre n'exerce pas d'attraction sur elle-même..

Certes.
Mais à quelle concentration ? (c'est une boutade, pas une question)
Les disgressions sur la physique quantique ont été écartées de cette discussion au post #1

@Albanxiii
Il n'est pas question d'un problème de masses variables, mais de deux objets, l'un d'une masse très petite en rapport d'une autre de masse très grande dont les masses et dimensions respectives ne changent pas. Seule variable la distance d entre leurs centres de gravité.

pour conclure cette salve de contributions :
Pour l'instant, une unanimité se dégage : pas de contradiction entre les eux grands hommes, mais le nb d'avis est encore un peu faible pour tracer la courbe gaussienne des opinions des Physiciens !!!
Merci de vos contributions qui me surprennent par leur richesse.

Ladrix.

[ThM55]

Donc Gauss n'aurait aucun mérite avec son théorème?

Si car il est plus général, il peut s'appliquer à une surface fermée quelconque, par forcément une sphère. Il relie le flux de l'accélération de la gravité à travers cette surface à la masse contenue à l'intérieur: . Gauss l'avait formulé pour l'électrostatique mais comme les lois sont semblables mathématiquement on peut transposer à la gravitation. La loi est équivalente à l'équation de Laplace pour le potentiel.

[stefjm]

Et histoire de citer un autre grand homme : Kepler.
Le flux de l'accélération de la gravité est une grandeur chrono-géométrique qui permet de définir la masse grâce à G.
et cette relation a été intuité par Kepler : https://fr.wikipedia.org/wiki/Lois_d..._p%C3%A9riodes

[Ladrix]

Bonsoir.

@ThM55
Merci de ces précisions.
Mais je ferais une remarque de fond.
En effet dans tout ce qui précède, il est toujours postulé depuis Newton que c'est un flux sortant du centre de la sphère cad d'un point sans grandeur physique qui ne contient rien et que ce flux se dirigerai donc obligatoirement vers la surface de la dite sphère (ou autre forme) et s'extrairait alors vers l'extérieur ou il se manifesterai jusqu'a l'infini de manière décroissante en 1/x².
Mon point de vue heuristique sur la question est différent.
J'opterai sur l'option non choisie par Newton celle d'un flux extérieur pénétrant vers le centre tout autant suivant une règle en 1/x².
En fait dans "de la Gravitation" il n'opte pour aucune des deux options estimant que dans le cadre de son travail, la causalité lui était indifférente et que de toutes façons, l'un ou l'autre option apportait la même réponse de variation et de valeur scalaire de la "force" dont il traite.
Aussi sur cette base de flux entrant, mes conclusions sont différentes des Physiciens autorisés sur le concept de la dite gravitation.
Seuls les faits sont pertinents, ce sont les mêmes du moins à ce point de la question. (350 ans de gestation non terminée)
Il aborde d'ailleurs son approche d'un point de vue géométrique, ce qui montre qu'a ses yeux, la causalité de la gravitation ne troublait pas ses pensées (en fait si, c'était un génie).
Je ne peux qu'approuver cette démarche car il s'était fixé comme tâche, il me semble, que de décrire les effets du phénomène et non ses causes.
1/3 de millénaire plus tard, la question ce pose, si on s'était trompé de choix du sens du flux?

Mais ce n'était pas la question initiale que je posais en #1.
Bien sûr c'était une entrée en matière avec une question aguicheuse...
J'aime votre approche qui traite de l'accélération, vision plus pertinente que le concept magique de "force".

@stefjm
Merci de rappeler que Newton ne partait pas de rien.
En fait on utilise µ =GM pour lever l'incertitude sur les deux grandeurs.

@ArchoZaure
je reviens sur votre post #5
Immense merci pour votre message qui m'aura orienté sur https://en.wikipedia.org/wiki/Shell_theorem
Heureusement que je ne connaissais pas cette page car celà m'a obligé à beaucoup réfléchir avant de me lancer dans des recherches ouvrageuses. En effet, j'aurais probablement laissé tomber mon travail, pensant mes objections balayée par ce remarquable travail.
J'arrête là cette réponse car je suis en train de digérer le lien...


Bonne soirée à tous
Ladrix

[gts2]

1/3 de millénaire plus tard, la question ce pose, si on s'était trompé de choix du sens du flux ?

Qu'entendez-vous par là ?
Que la gravitation est répulsive, non attractive.
Si c'est le théorème du flux sortant, c'est juste une convention, on peut prendre le flux entrant, cela donne flux de g= + 4 pi G M(intérieur)

[ThM55]

Oui c'est une pure convention: un flux "sortant" est un flux "entrant" compté avec le signe négatif. D'abord les maths. Ensuite la physique. Ce n'est pas sans raisons qu'on le fait dans cet ordre pendant les études.

[Ladrix]

C'est la nuit.
Un dernier passage.
@gts2
Il ne s'agit pas dans mon esprit de la convention du signe du flux, mais de sa réalité physique donc de sa source réelle.

@ThM55
même remarque.

Newton nous dit (de mémoire, demain je chercherai (peut être)la citation exacte)
"Je ne peux choisir entre une "force attractive venant du centre et une force répulsive venant de la périphérie, le résultat est pour moi le même, je ne tranche pas".
Certes, c'est pareil sur la courbe qu'on trace. Mais y a nuance sur l'origine du phénomène.
Dans un cas il faut sa loupe, son microscope à balayage pour examiner là ou y a rien, le point centrale de la planète, de l'étoile, du trou noir, dans l'autre, faut son télescope interférométrique braqué sur les confins observables de notre si bel Univers.
Pour le matheux (ce n'est pas péjoratif) c'est la même courbe, la causalité ne le concerne pas dans son domaine. Pour le Physicien qui cherche comme Max Planck la causalité stricte, la différence est entre la réussite et l'échec à terme de ses recherches.
Pour ma part, je ne tranche pas, je n'en sais pas encore assez sur le flux concerné pour avoir un avis motivé, les deux sont à mes yeux envisageable. (En fait je suis hostile comme Newton au concept d'une force attractive à distance sans support matériel et je rajoute par dessus : venant d'un lieu ou il n'y a strictement plus rien. (avis très personnel))

Sur la succession des priorités dans les études, il est certain que les mathématiques sont prioritaires. c'est l'outil pour traiter les données et les comprendre. J'avoue que je complète difficilement mon niveau math sur le tard, mais j'ai parfois des aides extérieures... (mon Pc calcule très très vite si on le cajole) de plus ces carences m'obligent à bien cerner les concepts avant de me lancer.
Dans l'exercice du Physicien, il me semble que la priorité est inverse, dans le sens ou le concept du chercheur prime le calcul, ceci s'entendant après collecte des données bien sûr.

Là je coupe c'est vraiment la nuit.

Ladrix

[choom]

Bonjour à tous, bonjour Ladrix.

Peut-être les 2 réflexions suivantes peuvent-elles aider à la discussion ou bien la compliquent-elles inutilement ?
En espérant que leur naïveté aide.

1. Le processus de formation d’une planète par accrétion progressive de matières précédemment disjointes :

Cela vous semble-t-il sensé d’imaginer des multitudes de forces extérieures s’exerçant sur chacune des particules formant un nuage de matière et pour chacune avec un vecteur différent depuis tous les confins de l’univers pour rassembler les uns vers les autres les corpuscules vers leur futur centre de gravité commun ?

Personnellement cela heurte mon esprit et s’apparente à du masochisme intellectuel : pourquoi faire compliqué quand on peut faire simple, et considérer que ce sont les micromasses de toutes ces particules qui, depuis leurs centres respectifs produisent ces champs de gravitation dans toutes les directions semblables et qui en s’additionnant mutuellement en arrivent fatalement au rassemblement de ces matières jusqu’à la formation d’un corps unique, chacune se dirigeant vers là où la plus grande quantité de masse se trouve par rapport à elle.

Une fois ce principe admis comme le moins extravagant des deux, il n’y aurait aucune raison pour que ces forces de cohésion cessent une fois la planète formée, créant la pression dans les profondeurs avec une gravité résultante inversément proportionnelle à cette profondeur à l’intérieur de la planète : voir point 2.

2. Imaginons un grain de matière de masse et de dimension petite par rapport à la planète, bien délimité et confiné dans les profondeurs de celle-ci. Les forces à l’origine de l’accrétion n’ayant pas disparu par enchantement, le grain continue d’exercer son champ de gravitation sur ses voisins et de subir les leurs. Forcément, s’il n’est pas situé au centre, et que la masse de matière est répartie de manière homogène dans cette planète, il aura plus de voisins du côté du centre que vers la périphérie et si on le déplace vers le centre il verra son ‘poids’ diminuer au fur et à mesure que le nombre de ses voisins s’équilibre entre toutes les directions.
Mais même si, au centre, la résultante des forces auxquelles il est soumis sera nulle et qu’il semble ne plus subir de gravité, il reste soumis à toutes les forces d’attraction importantes exercées depuis tous ses voisins dans la planète.

Sans rien avoir prouvé pour autant, j’espère avoir plaidé la préférence pour considérer que les forces de gravitations sont bien originaires des lieux de matières massiques et non de forces anti-matières provenant des confins de l’univers.

Bien cordialement.
Choom

[Ladrix]

Bonjour

@Choom
Meci pour ce moment de poésie.
Vous devriez envoyer ce message à Newton qui doit disposer de son dernier Nécrophone 5g comme tous nos ancêtres scientifiques.
Mais, si la théorie de l'acrétion n'est pas nouvelle, ce n'est pas l'objet de ce file.

Cela vous semble-t-il sensé d’imaginer des multitudes de forces extérieures s’exerçant sur chacune des particules formant un nuage de matière et pour chacune avec un vecteur différent depuis tous les confins de l’univers pour rassembler les uns vers les autres les corpuscules vers leur futur centre de gravité commun ?

La remarque est judicieuse.

Cela vous semble-t-il sensé d’imaginer des multitudes de forces intérieures s’exerçant de chacune des particules formant un nuage de matière et pour chacune avec un vecteur différent depuis tous les confins de l’univers pour rassembler les uns vers les autres les corpuscules vers leur centre de gravité commun ?

Vous avez raison celà semble insensé, mais si c'est insensé dans un sens, celà l'est tout autant sinon plus dans un autre.
La question du sens des interactions ne peut se résoudre par une pirouette de logique de comptoir. Et la question restera en suspend tant que la causalité de la gravitation ne sera pas résolue. Mais ce n'est pas la question du jour.

Sans rien avoir prouvé pour autant, j’espère avoir plaidé la préférence pour considérer que les forces de gravitations sont bien originaires des lieux de matières massiques et non de forces anti-matières provenant des confins de l’univers.

La préférence d'une thèse ou d'une autre n'est pas pertinente, et la qualification de "forces antimatière" me parait bien étrange.
Quand un badeau (moi par exemple) regarde les étoiles, il reçoit de la lumière provenant des confins (proches) de l'Univers, ce ne sont pas pour autant des forces antimatières qui frappent ses yeux ...
Ceci dit, merci pour cette disgression sympathique.

La nuit porte conseil et je reviens sur ma réponse à gts2 et ThM55 mon post #16
Il me semble qu'en fait le "flux" dont nous parlons ne serait pas le même pour les uns et pour les autres.
En effet, ce que mes correspondants traitent sous le nom de "Flux" serait un gradient de champ (gravitationel), alors que dans mon esprit je parle d'un fux entrant ou sortant réellement d'un objet, en l'occurence de l'énergie cinétique.
Pour un gradient, le sens est conventionnel, pour un flux d'énergie, c'est un transfert physique, le sens est réellement entrant ou sortant.
Ainsi, une fois de plus, Korzibsky avait raison, la carte n'est pas le territoire, il convient de bien préciser le sens (sic) des mots qu'on utilise...

Ladrix

Ps
il existe une expérience de pensée (de moi) qui semble montrer que l'accélération gravitationelle serait d'origine externe, mais ce n'est pas le lieu ici d'en débattre. Cette autre discussion pourrait se dérouler sur le forum Discussions scientifiques mais avec beaucoup de circonspection.

[albanxiii]

@Albanxiii
Il n'est pas question d'un problème de masses variables, mais de deux objets, l'un d'une masse très petite en rapport d'une autre de masse très grande dont les masses et dimensions respectives ne changent pas. Seule variable la distance d entre leurs centres de gravité.

Merci pour cette précision.
Ma question se pose toujours : pouvez-vous rendre la distance entre leurs centre de gravité aussi petite que vous voulez ? Et quelle est la masse à prendre en compte pour chaque valeur de cette distance ?

Ou bien : quel est le champ de gravitation engendré par une coquille sphérique en un point de son intérieur ? Pour commencer on peut considérer le centre.


ps : la formulation me gêne, on ne fait pas un sondage pour savoir qui a raison, on est dans le domaine des sciences, on a les moyens de trancher.

[gts2]

Il me semble qu'en fait le "flux" dont nous parlons ne serait pas le même pour les uns et pour les autres.
En effet, ce que mes correspondants traitent sous le nom de "Flux" serait un gradient de champ (gravitationel).

Le flux dont je parle est le flux du théorème de Gauss, puisqu'on est parti de là, et ce flux est le flux du champ gravitationnel : produit scalaire de la surface et du champ (donc un scalaire).

[oualos]

Ça a bien l'air d'un faux problème tout ça, s'cusez du peu: pour calculer les mouvements des planètes, on s'est servi d'un artefact -dont on se sert toujours- à savoir ramener la masse en son centre de gravité.
et du coup la cinématique -science exacte s'il en est- permet de calculer des mouvements en mécanique classique comme évidemment ceux des planètes qui intéressait Newton et une flopée d'autres.
Je réitère et persiste: si les distances diminuent trop entre 2 masses -ou pour une seule masse en s'approchant du centre de gravité- il se passe l'inverse de la décohérence quantique c.-à-d. que vient un moment on est obligé de prendre en compte d'autres forces que gravitationnelles soit électromagnétiques.
Et plus on descend dans l'échelle, plus les forces gravitationnelles deviennent négligeables relativement à l'électromagnétisme.
Je vois pas où est le problème dans tout ça.
sinon on fait une expérience de pensée mais vraiment pour le coup sans grand intérêt: avec quoi et comment va-t-on s'approcher indéfiniment du centre de gravité de telle ou telle planète... ou boule de billard ou ce que vous voulez ?
Surtout pour prouver quoi ? Ce ne sont pas des formules même si elles sont extrêmement intelligentes qui vont nous aider à trouver une réponse....

[Ladrix]

Bonjour.

@oualos
Merci de votre contribution.
Je rappelle que l'approche de la gravitation dont il st ici question est dans le cadre de la mécanique classique comme précisé en #1

@gts2
Merci de confirmer mon intuition, nos définition de "flux" ne sont pas compatibles, ce qui ne serait un problème que si on l'ignorait.

@Albanxiii

Ma question se pose toujours : pouvez-vous rendre la distance entre leurs centre de gravité aussi petite que vous voulez ? Et quelle est la masse à prendre en compte pour chaque valeur de cette distance ?

Newton y arrivait, Gauss aussi, je suit la voie tracée, mon projectile se déplace dans la cible librement sur une trajectoire purement axiale.
Les conditions sont que les masses en présence sont considérées constante (les vitesses sont réputées << c et les masses usuelles comme le vélo d'Armstrong et la Lune)
La distance entre les deux objets sont définies par la distance entre le point du projectile réputé ponctuel et le centre de gravité de la sphère cible qui est confondu (pour une sphère homogène et isotrope) avec son centre géométrique.
Vous allez m'objecter que mon projectile s'écrase sur la surface de la sphère. Certes, mais pas plus que les masses de Newton et Gauss, mais j'ai un avantage, mon projectile est un perforant de dernière génération uranium appauvri chemisé carbure de tungstène, un peu cher mais très performant.
Passons aux choses sérieuses.
Les coquilles vides.
C'est un domaine intéressant coté gravitation.
Gauss en aura traité dans son théorème de la Gravitation.
Il affirme que dans une coquille vide, etc...
Je confirme présentement qu'il a raison quand au résultat :
en tout lieu du vide de la coquille, l'accélération locale de la gravitation est nulle.
Son explication est, dans l'énoncé dont je dispose plutôt indigent, mais la solution est exacte.
Le traitement d'une coquille vide d'épaiseur nulle et de masse = à une sphère pleine est fort intéressante, mais hors sujet.

Cette courbe est tracée sur la base de la formule de Newton tenant compte de la dispersion de la masse dans un volume
F=GMM'/(x²+y²)^3/2
qui donne après passage de force à accélération ma très belle fonction symétrique en x versus y
A = -yx/(x²+y²)(x²+y²)^1/2
A accélération, M masse d'un élément, x position axiale du projectile (centre x=0), y position radiale de l'élément considéré et masse de l'agrégat des éléments d'un y donné.
Le signe - normalise l'accélération positive quand v augmente et inversement.
Formule que j'ai trouvée tout seul comme un grand en plus court que la longue démonstration de Newton himself dans les Principia (Source Shell_theorem dont j'ai pris connaissance hier grâce à ArchoZaure #5)
A noter l'esprit de géomètre de Newton, qui se complique la vie avec ses démonstrations des plus ouvrageuses sinon absconces, mais de très belles animations (inutiles) sur la page Wiki.
Sur la base de cette fonction, j'établi la somme (j'intègre numériquement) les résultats d'une belle sphère de 4/3*2* pi *10e9 éléments sur une tajectoire de 10 E4 points . Vous remarquerez le nb de calculs que celà nécessite, en précisant que le calcul d'un point prend dans les 50ns sur mon surface go3 à 420 euros.
nb de points de la sphère
6 981 317 007,9773183076947630 739545
on négligera par obligation des éléments finis la chiquette finale
6 981 317 007
Je calcule tous les 1/1000 de rayon pour une bonne précision, sur une une distance de +-5 rayons de la dite sphère.
Au dela 1/x² convient très bien, l'écart devient insignifiant.

On applique cette fonction à une sphère extérieure de rayon 1 puis à une sphère intérieure de rayon 0<r<1
Ceci fait on déduit les résutats de intérieur des résultats de extérieur et ça fait le beau tracé que vous ne manquerez d'admirer longuement.
Pour agacer je rajoute que tout ce fourbi monstrueux ne me prend (à mon Pc) que 1 seconde environ. Comme ici on ne traite pas de mes algos, j'en resterai là.
Note finale
Cette courbe indique l'accélération gravitationelle f(x) elle ne permet donc pas directement de calculer la vitesse de chute ni l'énergie cinétique du projectile but de ces ouvrageux calculs.
Il convient donc de traiter ensuite les données (un beau tableau de réal) pour transformer le f(x) en f(t) pour ensuite intégrer et finir le travail, qui sera complété par l'étude des dérivées, encore de belles heures de programmation en perspective et surtout d'interprétation des résultats.
Comme je suis (très malin), je sais aussi faire les courbes pour des objets non sphériques, c'est fun...

note finale bis
je reviens sur l'explication de la chose par Gauss.
Ses raisons géométriques, pour justes qu'elles puissent être, ne sont pas celle d'un Physicien, mais d'un mathématicien cad a-causales.
Ma méthode de calcul éclaire cette question de causalité, mais ce n'est pas l'objet de ce file.

Pour conclure cette conclusion
Il apparait que la question que j'ai posée hier était due à un manque de connaissance de ma part des détails du travail de Newton et de celui de Gauss.
J'ai donc une réponse à cette question :
Il n'y aura jamais eu oppostion entre Newton et Gauss sur le sujet de la Gravitation.
Voilà.
Mais reste une question angoissante (?) : la décroissance de la "force" gravitationelle jusqu'a 0 dans un objet massique (pléonasme) est-il bien pris en compte de nos jours par les Physiciens ???

votre dévoué (à la science) Ladrix

[ThM55]

Mais reste une question angoissante (?) : la décroissance de la "force" gravitationelle jusqu'a 0 dans un objet massique (pléonasme) est-il bien pris en compte de nos jours par les Physiciens ???

Je peux te rassurer et clamer tes angoisses: oui!

Sinon, comment ferait-on des modèles des étoiles, dont le soleil? Suffit d'ouvrir un traité élémentaire d'introduction à l'astrophysique.

[Ladrix]

@thM55
Bonjour
je n'ai pas d'angoisse, tout va bien.
Aussi je lis à "effondrement gravitationnel" que celui-ci de déclenche par le milieu soumis à etc... etc... alors qu'à cet endroit la gravitation devient quasi nulle... Mais j'ai dû rater un épisode...
Merci quand même du réconfort.

Ladrix

[gts2]

Je ne comprends pas trop votre calcul : vous dites que c'est purement axiale (selon l'axe x je suppose) et donc y=0 ?
A l'extérieur, c'est toujours 1/r², non ?

[stefjm]

Je ne comprends pas trop votre calcul : vous dites que c'est purement axiale (selon l'axe x je suppose) et donc y=0 ?
A l'extérieur, c'est toujours 1/r², non ?

J'ai le même doute.
Pourquoi y aurait-il une différence par rapport à 1/r^2 à l'extérieur?

[Ladrix]

@gts2
C'est la trajectoire du projectile qui est sur l'axe généré par sa propre position spatiale et le centre de la sphère cible.
La valeur y représente la position radiale des éléments finis de la tranche de sphère de position x.
Je viens d'apprendre que Newton avait pratiqué de même.

@stefjm
La question était celle posée à l'origine de mes travaux il y a déjà 1 an.
Voilà comment j'abordais la question de Newton : la fonction vaut inf pour x=0.
Celà contrevient à une opinion personnelle : en mathématique ok, en physique verbotten.
Je compute et recompute, je progresse et trace la fonction :
y = x/(x²+y²) ^3/2 qui correspond à 1/x² projeté sur l'axe des x
Je trace : c'est beau, quasi voluptueux, ça ressemble à 1/x² ça s'incurve, ça vaut y=0 pour x=0 et ça continue en -/x²
Merveilleux et galbé...
Plus qu'a tenir compte de la forme sphérique.
Mais là je cafouille dans mes visualisations et même dans mon algo de calcul.
Je fais un break.
Un physicien quasi autorisé (thésard) passe par hasard dans mon terrier.
On discute.
Quelque temps après il me communique le théorème de Gauss. Je suis ignare, encore un truc inconnu...
Cette droite me révulse. Un texte (privé) vengeur traite de cette horreur.
Après ça, je m'y remet, à partir de 0.
Très rapidement je viens à bout des questions techniques et surtout de l'écriture d'un logiciel pour confirmer/infirmer mon travail.
Un beau soir, tout est bon.
Je trace ma 1ère courbe de -5 rayons à +5 rayons par incrémements d'un millième de rayon. Je suis un génie, ça prend le temps d'afficher les pixels... en fait 3 secondes. (je calcule beaucoup de points)
J'ai une trace de 10 000 pixels sur 1000 qui défile sur mon screen.
Et là horreur, mes belles rondeurs se cumulent en une courbe conjugant la 1/x² de Newton et la x de Gauss avec un raccordement en rebroussement en x=r, bien symétrique en 0,0 c'est un grand choc...
Il m'aura fallu 1 semaine pour m'en remettre.
après contrôle de toute ma machinerie, tout est correcte, la courbe est bien la bonne...
Restait à savoir pourquoi cette forme surprenante.
J'ai ajouté 4 lignes à mon programme pour les courbes et quelques unes à la visualisation pour compendre la raison de cette surprise.
En fait, quand le projectile arrive à la surface de la sphère, toute la sphère participe à son accélération.
Au premier pas à l'intérieur, la masse qui attire par devant décroit et il apparait à l'arriere une calotte sphérique qui commence à freiner le projectile.
Je trace la courbe de ce qui accelère et une autre de ce qui freine.
On obtient deux courbes en forme de dent de requin symétriques en 0,0 cad rotées de 180°.
Les deux accelérations s'ajoutent, bien sûr et, miracle la somme est une droite en x...
Cette courbe n'est droite que pour une ellipsoïde de révolution, donc une sphère, ça gondole parfois beaucoup pour d'autres profils.
Ainsi la causalité de la droite de Gauss n'est pas gèométrique mais physique. C'est l'application stricte de la loi de Newton sans artifice aucun.
J'accepte les applauses.
voici le résultat statique



C'est le même calcul qui donne la courbe avant de pénétrer la sphère que celui qui calcul dans la sphère, et que celui qui calcule en ressortant de l'autre coté.
En fait, je scanne la forme de profile qui est un cercle sur une base de donnée du "champ gravitationnel" d'un très long cylindre qui est long de tout le trajet prévu pour le projectile. Cool.
Une démo vidéo sera réalisée par mes soins, la 1ère est un peu bidulique je reste pudique.

Ladrix

[gts2]

@gts2
C'est la trajectoire du projectile qui est sur l'axe généré par sa propre position spatiale et le centre de la sphère cible.
La valeur y représente la position radiale des éléments finis de la tranche de sphère de position x.

Donc la trajectoire est radiale et la position sur cet axe est repéré par x avec x=0 le centre de la sphère ?
Le tracé est celui de l'accélération ? Si oui, à l'extérieur de la sphère, celle-ci vaut 1/x², pas approximativement mais exactement tant qu'on est à l'extérieur.
Si non, c'est le tracé de quoi ?

[Ladrix]

Salut.
@gts2
Des questions très pertinentes.
Je dois cependant préciser que je ne suis pas prof de math ni de physique et que je n'exprime que des avis personnels.

Donc la trajectoire est radiale et la position sur cet axe est repéré par x avec x=0 le centre de la sphère ?

oui, le projectile est réputé suivre ce trajet, en fait c'est son trajet qui détermine les axes x et y du référentiel dont le point 0,0 est le cetre de la cible.

Le tracé est celui de l'accélération ? Si oui, à l'extérieur de la sphère, celle-ci vaut 1/x2, pas approximativement mais exactement tant qu'on est à l'extérieur.
Si non, c'est le tracé de quoi ?

Oui, c'est la courbe de l'accélération qui est strictement la même que celle de la "force" puisque la masse du projectile étant constante pour un objet donné, je n'en tient pas compte. Masse =1 accélération= 1 à la position x=-r si la cible, la sphère avait sa masse concentrée en x=0.
Comme ce n'est pas 1/x² je précise ce que c'est :
La masse de la sphère cible n'est pas ponctuelle la courbe extérieure n'est donc pas strictement 1/x².
On peut voir qu'en fait, la courbe qui est tracée est en dessous de la courbe 1/x² que je trace systématiquement comme référence.
Si la matière n'était pas disséminée dans la sphère, cad concentrée au point 0,0 de la sphère, la courbe de l'accélération serait confondue avec 1/x² jusqu'en x=-r et passerait à une ligne droite de fonction y=-x jusqu'a la sortie de l'autre coté de la cible.
Comme on peut le voir, ma courbe ne vaut pas 1 à x=-1 et y= -1 à x=1, mais 0.9 environ. Pour la démonstration j'ai interrompu les calculs dans la sphère, sinon on voit rien ...
Ce qu'il faut bien comprendre, c'est que ce qui manque à l'accélération par rapport à 1/x² en arrivant au contact de la sphère est la partie d'accélération qui est à l'intérieur.
Comme la courbe traite de l'accélération A f(d) et non de A f(t) c'est pas évident de s'en rendre compte.
Regarder la courbe plus haut sur la sphère creuse c'est plus visible.
Bien sûr, je vais rajouter un "petit" calcul pour traduire f(d) en f(t) comme indiqué dans un précédent post.

pour conclure
Il est facile de voir qu'au contact de la sphère, l'accélération est inférieure à celle donnée par Newton car on est dans le cas d'un objet non ponctuel. Ce que Newton avait prévu et prévenu tout son monde : "ma fonction n'est valide que pour des objets très éloignés en proportion de leur taille". Comme il traitait des planètes, il négligeait l'écart de très près.
J'ai vérifié, à distance de 5 rayons l'écart de la courbe corrigée est infîme par rapport à 1/x².

Voilà, en espérant avoir bien éclairé les questions posées.

Ladrix.

[gts2]

La masse de la sphère cible n'est pas ponctuelle la courbe extérieure n'est donc pas strictement 1/x².

SI c'est une sphère de symétrie sphérique si.

On peut voir qu'en fait, la courbe qui est tracée est en dessous de la courbe 1/x² que je trace systématiquement comme référence.

Donc il y a une erreur quelque part, ou des problèmes liés à la discrétisation de la sphère.

Ce qu'il faut bien comprendre, c'est que ce qui manque à l'accélération par rapport à 1/x² en arrivant au contact de la sphère est la partie d'accélération qui est à l'intérieur.

Je répète, non, d'après Gauss, à l'extérieur c'est 1/x²

Il est facile de voir qu'au contact de la sphère, l'accélération est inférieure à celle donnée par Newton car on est dans le cas d'un objet non ponctuel.

Encore une fois non.

Ce que Newton avait prévu et prévenu tout son monde : "ma fonction n'est valide que pour des objets très éloignés en proportion de leur taille".

Newton avait aussi prévu que pour une sphère (proposition 71) : la force gravitationnelle d’un corps qui se trouve à l’extérieur d’une couche sphérique fermée de matière est la même que ce qu’elle serait si toute la matière de la couche était rassemblée en son centre.