Déterminer formule de température d'une particule

[MyL38]

Bonjour,

Je souhaiterais svp solliciter votre aide afin de trouver une expression qui me permettra de déterminer la température d'une particule car je pense qu'il y a du calcul infinitésimal qui entre en jeu, et je ne maitrise pas super bien cet aspect.

Sachant que je ne suis pas doué pour les explications, voici une image qui permettra une meilleure compréhension pour la suite


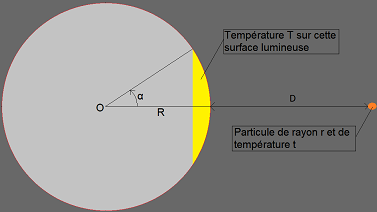
Sur cette image nous avons une grande sphère qui peut produire un rayonnement sur une partie de sa surface (en jaune), en fonction de l'angle Alpha. Ce rayonnement est de même intensité partout sur la zone concernée (en jaune).
Et à une distance D de la surface de cette sphère, il y a une petite particule de rayon r et de température t, et d'albédo a (que j'ai oublié de mettre sur le dessin).

Je crois savoir que dans le cas d'une particule chauffée par une étoile, il est possible de déterminer la température de la particule en fonction :
- du rayon de l'étoile,
- de la température de surface de l'étoile,
- de la distance entre la particule et l'étoile,
- de l'albédo de la particule.

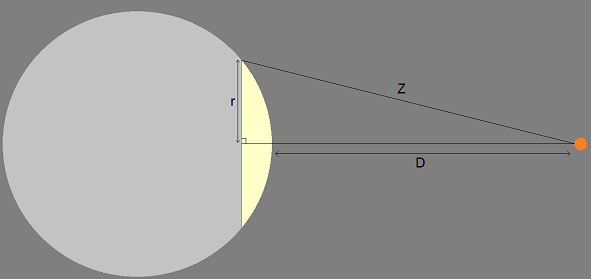
Seulement ici, ma difficulté est que, sur la partie rayonnante déterminée par Alpha, tous les points ne sont pas à distance D de la particule. Je pense que la complexité de ce problème est au delà de mes compétences. Mais j'ai réellement besoin de déterminer l'expression de la température de la particule, en fonction des paramètres de l'image (et de l'albédo).
Pourriez-vous m'aider ? Ou m'aiguiller ? 
Merci par avance.
-----

[NeOZSSJ]

Bonjour, j'ai peut être un élément de réponse.

Pour le calcul de la surface j'ai fait une soustraction de deux surfaces, la première étant la surface totale tandis que la deuxième est celle de deux triangles rectangles. SI tu veux trouver par toi même, je te conseille de travailler sur une partie puisqu'il y a symétrie par rapport au rayon. SI tu veux la réponse la voila :

J'ai trouvé à l'aide de on raisonnement qui est peut être faux que l'aire de la surface jaune vaut R²(alpha - sin(alpha)cos(alpha))

Voila, hésite pas à refaire le calcul ou à attendre la réponse d'autres personnes pour être sûre du résultat.

Bonne journée

[XK150]

Salut ,

Je vois le principe du calcul de cette façon : Il faut calculer la contribution de chaque point émetteur .

Il faut diviser la calotte sphérique émettrice en couronnes concentriques de largeur infiniment mince .
Faire le calcul pour un point de la couronne et multiplier par la longueur de la couronne .
Faire la somme pour toutes les couronnes .

PS : demander à un modo par mp de déplacer votre question en math .

[MyL38]

J'avais posté dans le forum de physique car il y a quand même des notions de physique que je ne maitrise pas forcément.

Alors j'y ai réfléchi depuis 3 jours mais j'ai vraiment du mal, je ne sais même pas par où commencer.
Bon voici quand même quelque chose (même si il y a de grandes chances que ça soit tout faux je préviens ) :

La loi de Stefan dit que la puissance délivrée par unité de surface s'exprime de cette façon : P = σ.T⁴
Où P est en W/m², σ est la constante de Stefan, et T est la température de la surface émettrice du rayonnement en K.

Si on décompose la calotte en plusieurs petits cercles, alors pour un point infiniment petit du cercle (un dl du cercle) on aurait une puissance de : dP = dl.σ.T⁴
(Donc le dP serait en W/m...? Déjà juste là, je ne sais pas dans quoi je m'embarque...)

Or notre particule ne va pas capter toute cette puissance car elle se situe à une distance Z des points du premier cercle :


Par conséquent, il faut supposer que ce point du cercle est le centre d'une sphère sur laquelle se trouve notre particule (donc une sphère de rayon Z), et diviser cette puissance élémentaire par la surface de cette sphère (4.π.Z²). Donc la puissance reçue par notre particule, et par unité de surface serait de :

dP_Reçue = dl.σ.T⁴/(4.π.Z²)

Si on intègre cette puissance reçue sur tout le cercle de rayon r (voir l'image), alors on aurait une puissance de cercle : P_cercle = 2.π.r.σ.T⁴/(4.π.Z²) = r.σ.T⁴/(2.Z²)
(Et là on se retrouve avec un P en W/m³, ça ne va pas du tout...)

Je suis persuadé que j'ai tout faut, mais c'est pour dire à quel point je suis largué...

De plus pour la suite, je ne sais pas comment avoir une surface élémentaire avec un bout de sphère.
Et pour les paramètres Z, r, D, Alpha, R c'est complètement arbitraire, je considère simplement que le but final est de déterminer la température de la particule, à une distance donnée, et pour une calotte donnée (déterminée donc par un angle Alpha par exemple).

[A voir en vidéo sur Futura]

[gg0]

Bonjour.

Le problème mathématique sera vite résolu si tu traites le double problème physique qui est :
1) Quelle est l'énergie reçue par la particule, en un temps donné, d'une portion de surface ds (en intégrant cette énergie sur toute la surface éclairante, on obtiendra l'énergie totale reçue) ? Cette énergie dépend évidemment de la position de ds dans la partie jaune.
2) quelle sera la température de la particule sachant quelle reçoit cette énergie dans ce temps ?

Les matheux ne sont pas des spécialistes de la chaleur et de l'optique. Par contre, ils savent définir une surface élémentaire de la sphère à partir de l'équation de la sphère, par exemple en coordonnées sphériques


Donc il vaut mieux faire remettre ce sujet en physique, poser les questions physiques, et, s'il y a un problème de calcul mathématique, revenir l'exposer ici. Mais, à ma connaissance, ceux qui savent poser le problème physique savent généralement faire ce genre de calculs, très courants en physique théorique.

Cordialement.

[MyL38]

J'ai des difficultés autant en maths qu'en physique, mais en effet je pense que le sujet doit être dans le forum de physique, là où je l'avais posté initialement (il a été déplacé). Si vous pouviez le déplacer en Physique ça serait sympa

Pour vous répondre gg0 :

1) Alors tout d'abord, je sais comment faire si je me base sur une étoile en entier, la puissance qu'elle délivre dans toutes les directions s'exprime de cette façon : P_étoile = 4.π.R².σ.T⁴ (en W). Où R est le rayon de l'étoile, et T sa température de surface.
Ensuite, pour connaitre la puissance que reçoit la particule (on va supposer que c'est un corps noir pur pour simplifier), il faut imaginer que le centre de l'étoile est aussi le centre d'une plus grande sphère sur laquelle la particule se trouve à sa surface, et donc il faut diviser la puissance de l'étoile par la surface de cette grande sphère pour avoir la puissance par unité de surface, on aurait donc :
P_{unité de surface} = 4.π.R².σ.T⁴/(4.π.d²) = R².σ.T⁴ /d² (en W/m²). Où d est la distance entre l'étoile et la particule.
Il faut ensuite multiplier ce résultat par la section droite que représente la particule, disons simplement que cette section est de π.r², et donc la particule reçoit P_reçue = π.r².R².σ.T⁴/d² (en W).

Seulement, cette particule ne fait pas que recevoir de la puissance sinon sa température ne fera que monter. Pour avoir une température stable, la particule rayonne la même puissance qu'elle reçoit P_reçue = P_rayonnée = 4.π.r².σ.T⁴ _particule

Et de ces équations, on peut obtenir la température de la particule en isolant le T_particule.

Dans notre cas, je pense que nous pouvons déjà dire qu'une surface élémentaire de l'étoile émet une puissance élémentaire dP = dS.σ.T⁴.
Mais c'est plus complexe pour la suite, puis-je considérer une surface élémentaire comme un point qui rayonne dans tous les sens comme une sphère ?
Si oui, ça nous donnerait dP_{unité de surface} = dS.σ.T⁴/(4.π.d²) (sachant que d est variable puisqu'il représente la distance entre la particule et la surface élémentaire).

Et donc la puissance élémentaire reçue par la particule serait dP_reçue = π.r².dS.σ.T⁴/(4.π.d²) = r².dS.σ.T⁴/(4.d²)

2) Pour la température, on sait que la puissance reçue et la puissance rayonnée par la particule sont égales. On connait l'expression de la puissance rayonnée (qui contient T_particule), il nous faut maintenant intégrer la puissance reçue sur toute la surface, pour avoir une équation et sortir le T_particule (si bien sûr mon expression de dP_reçue est correcte).

[gg0]

Je ne suis pas administrateur, je vais simplement signaler le sujet.

"puis-je considérer une surface élémentaire comme un point qui rayonne dans tous les sens comme une sphère ?" oui, c'est le principe de Huyghens. Attention, pour un élément de surface, le rayonnement n'est pas isotrope. C'est là que je suis trop léger en physique. De même pour la suite des tes explications.

Cordialement.

[MyL38]

Oui je vois ce que vous voulez dire... J'avais en effet des doutes sur la surface d'une étoile parce que sur la page wiki ils disent qu'une étoile est isotrope, ça porte à confusion :https://fr.wikipedia.org/wiki/Source...%20%C3%A9toile.

Au moins maintenant les choses sont claires, l'étoile entière est isotrope, mais juste une partie de sa surface non.

Et par conséquent, je suppose qu'il va falloir prendre en compte un angle entre la normal de la surface élémentaire et la direction particule-surface élémentaire.
J'avais également vu sur wiki un sujet sur l'étendue géométrique :
https://fr.wikipedia.org/wiki/%C3%89...om%C3%A9trique

Mais je n'étais pas certain que ça s'appliquait à mon cas vu qu'une étoile, c'est la surface en incandescence qui fournit la lumière elle même (c'est pas comme le verre d'une ampoule comme leur exemple), donc j'avais des doutes également là dessus... En tout cas merci.

Du coup, si des personnes assez calés en optique et rayonnement thermique passaient par là Si je pouvais avoir un petit coup de pouce s'il vous plaît ? J'ai du dire beaucoup de bétises

[albanxiii]

JSi vous pouviez le déplacer en Physique ça serait sympa

Voilà, c'est fait. Merci à gg0 pour le signalement.

[ArchoZaure]

Bonjour.

Je ne comprends pas où vous voulez en venir avec cette histoire de "calotte" (déterminée par un angle alpha).
Car s'il s'agit d'une étoile l'énergie rayonnée à une distance D se calcule plus simplement.
Sur le principe vous avez une énergie produite par l'étoile, on connait cette quantité.

On calcule la surface TOTALE de l'étoile ce qui est facile si on connait son rayon R et on en déduit l'énergie rayonnée par unité de surface.
Ça c'est pour l'étoile, à sa surface, et pouvez vous en passer.

Mais vous pouvez appliquer ce même principe pour calculer l'énergie par unité de surface à une distance arbitraire, par exemple D
A une distance D vous avez une sphère (virtuelle) de rayon D+R qui présente une surface (à calculer)
A partir de là vous pouvez calculer, comme à la surface de l'étoile, l'énergie qui transite sur cette sphère par unité de surface.
Ensuite, pour savoir quelle est l'énergie reçue par votre "particule" (planète) c'est soit simple soit complexe.

1. Simple, l’albédo ne change pas selon l'angle d'incidence de l'éclairement de la particule :
C'est le cas par exemple si la surface est rugueuse (vous avez une planète couverte de forets par exemple).
Dans ce cas la surface de la particule équivaut à la section de la sphère (et non pas la surface même du sol), donc un disque ayant le rayon de la particule.
Il suffit donc de multiplier cette surface par l'énergie/surface de la sphère virtuelle à la distance D+R pour connaitre l'énergie reçue (par unité de temps bien entendu).
Et bien sur de multiplier par l'albédo.

2. Compliqué, l'albédo change selon l'angle d'incidence, là faut voir pour le calcul je sais pas dire comme ça.

[MyL38]

ArchoZaure, votre méthode est valable pour des distances suffisamment grande pour considérer l'étoile comme un simple point.
Par exemple, c'est valable pour la terre qui se situe à 150 000 000 de km du soleil, car le diamètre du soleil 1 400 000 km est suffisamment négligeable par rapport à la distance (on peut donc considérer le soleil comme un simple point qui fourni une puissance P=4.π.R².σ.T⁴).

En revanche, ce que moi j'essaye d'établir, c'est une loi qui donne la température d'un corps se situant à de faibles distance de l'étoile (de 0 à 10 000 000km pour le soleil).

J'ai de bonnes raisons de penser que l'élévation de la température de la couronne solaire vient simplement de ce problème de géométrie que pas mal de monde semble négliger.

Car en effet, à de faibles distance, on ne peut plus considérer le soleil comme un simple point. Supposons que nous nous trouvons à 1000km d'altitude, à cette distance, le soleil n'est plus un simple point situé à 697 000km (R + 1000km), mais c'est plutôt un mur de lumière gigantesque qu'on a en face de nous, qui nous bombarde de puissance lumineuse.

Voilà pourquoi j'essaye, à partir de la loi de Stefan, d'établir une loi qui détermine la température d'un corps en fonction de sa distance à la surface de l'étoile, de la température de l'étoile, et du rayon de l'étoile.
Beaucoup se demandent pourquoi en s'éloignant du soleil la température augmente, comme si nous étions en train de parler d'un chauffage... C'est complètement différent, ici ce qui réchauffe le corps, c'est la surface lumineuse du soleil, or justement, plus on s'éloigne du soleil, plus la surface qui bombarde le corps est grande (certes, la distance aussi mais...).

Si quelqu'un est intéressé par ce problème, je pense que si on étudiait un plan lumineux infini, on pourrait peut-être démontrer que la température d'un corps ne fera qu'augmenter avec la distance. C'est une idée à laquelle j'ai longtemps pensé mais je ne suis pas suffisamment à l'aise mathématiquement pour le démontrer, si quelqu'un est intéressé pour m'aider, n'hésitez pas à m'envoyer un message privé.

[gts2]

Bonjour,

Il faut aller voir du côté des "facteurs de forme" de rayonnement thermique.
Par ex. : math.upmc.fr/hecht/
Dans les annexes p. 41, vous devriez trouver ce que vous cherchez.