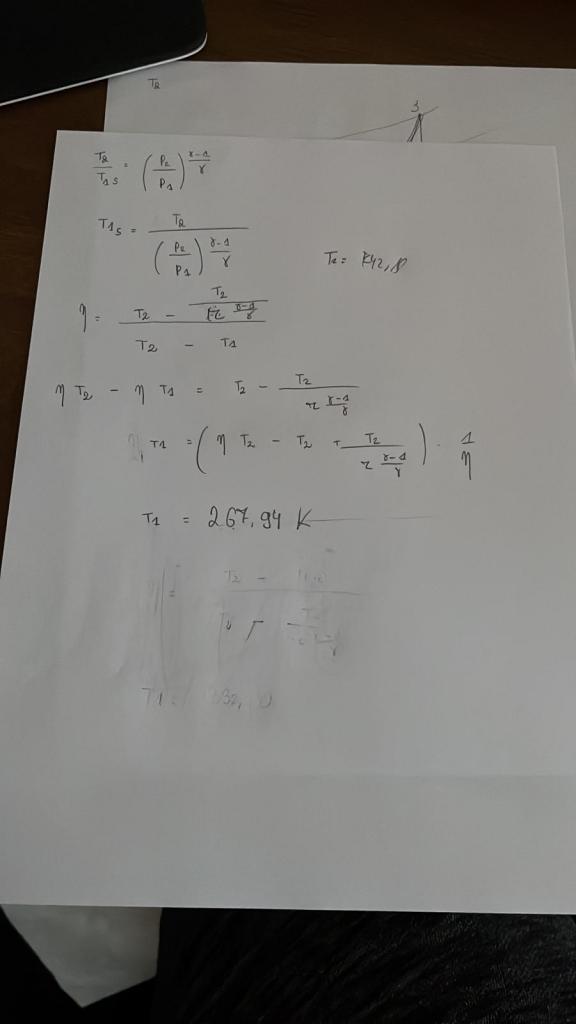Bonjour je cherche à résoudre ce problème :
Une turbine à gaz est alimentée par 100 [kg/s] d'air ambiant (1,05 [bar]). Le rapport de compression (p2) est de 23,5 et les gaz sont rejetés à l'atmosphère directement après la turbine. Le combustible utilisé est du méthane (CH4), également disponible à la température ambiante, et dont on négligera l'apport de masse. On considère une compression et une détente non idéales, le rendement isentropique de compression étant égal à 0,93 et le rendement isentropique de détente à 0,90. Les gaz sont tous assimilables à des gaz parfaits et ont les propriétés de l'air, à savoir un coefficient de chaleur massique à pression constante de 1,009 [kJ/kg·K] et une masse molaire de 28,97 [kg/kmol]. On vous demande de :
1. Esquisser qualitativement l'allure du cycle dans un diagramme (T,s).
2. La température de l'air en sortie du compresseur est mesurée à 469 [°C]. Quelle est la température de l'air ambiant ? Et quel est le travail moteur massique fourni par le compresseur (réponse en [kJ/kg]) ?
Je sais résoudre ce genre de question normalement mais là on me demande de chercher T1s sauf que je ne comprend pas vraiment comment le chercher. Normalement, j'utilise la formule suivante dans le cas d'un rendement isentropique pour le compresseur -> (T2s/T1) = (P2/P1)^((γ-1)/γ) et la deuxième formule est le rendement isentropique = 0,93 = T2s - T1/T2 - T1. De la je parvenais à trouver T2s et T2 mais là on me demande de déterminer T1s et T1 en me donnant T2 sauf que cette formule ne me permet pas vraiment. J'ai essayé de trouver directement T1 en faisant un système 0 2 équations et 2 inconnus mais cela me ne donne pas vraiment la bonne réponse.
N'y a t'il pas moyen de trouver directement T1s svp ?
Merci d'avance.
-----




 donne si T1 est connue
donne si T1 est connue