PFD : guidage le long d'une rainure

[cmole]

Bonjour à tous,

Je fais appelle à vos lumières car je fais face à un problème que j'ai un peu de mal à résoudre actuellement, si vous avez donc des pistes je suis preneur !

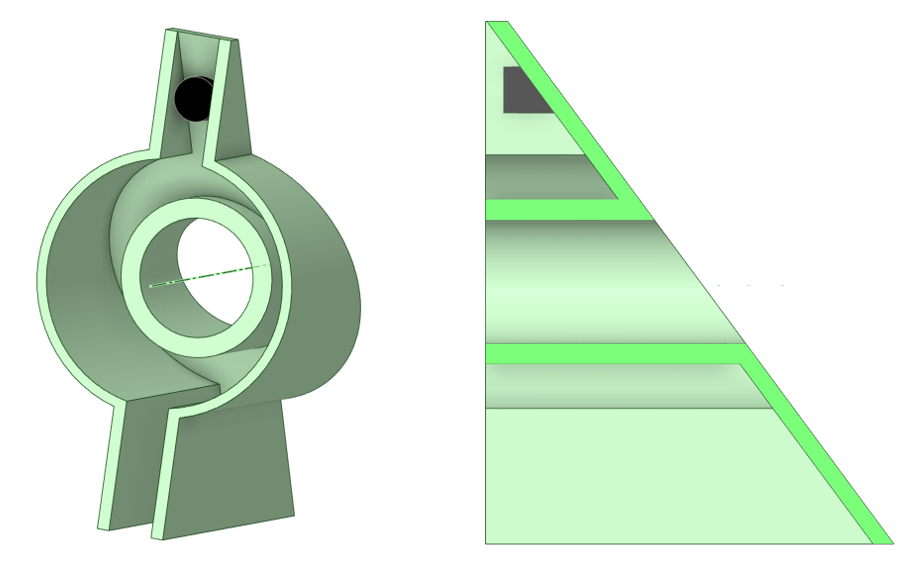
Le système étudié est une "pastille" (en noir dans la photo ci-dessous) qui se déplace le long d'une rainure. Cette pastille est soumise à une force (constante, pour simplifier la chose) et est en contact avec les bords de la structure (on considère que le contact n'a lieu que d'un seul côté), les frottements et la gravité sont négligés. Puisque la structure sur laquelle est appuyée la pastille est inclinée celle-ci va descendre et suivra la rainure. Voici un 3D, de principe et simplifié, pour éclairer un peu mes propos.

Pièce jointe 485708


L'objectif est donc de déterminer la position de la pastille en fonction du temps, à l'aide du PFD. Pour les rainures rectilignes aucun problème : il s'agit d'un glissement sur plan incliné. En revanche, pour la partie circulaire, j'ai un léger problème : je n'arrive pas à déterminer une force de contact. Voici le modèle et les équations auxquelles je suis parvenu :

Capture1.PNG

Capture2.JPG

Soit, en manipulant un peu les équations (exactement la même méthode que pour le glissement d'un inuit sur un igloo ) :

Capture3.JPG

Ici je ne pense pas m'être trompé puisque le résultat est analogue à l'inuit sur l'igloo, donc "tout va bien". C'est pour la suite que ça se corse : la détermination de N1. Puisqu'on a plus d'inconnues que d'équations, je me suis mis en tête de trouver une relation entre z" et θ pour trouver N1. La démarche suivie est la suivante :

Capture4.JPG

Et c'est là que ça bloque, car pour moi cette relation est fausse puisque je trouve, après calculs (que je ne détaille pas ici, mais au besoin je peux le faire) que N1 est fonction de l'angle θ. Or, pour moi (et c'est peut être là aussi une erreur), N1 devrait être constant et ne dépendre que de la force F et de l'angle phi. Est-ce correct ? si oui, quelqu'un saurait où se trouve mon erreur de raisonnement ?

Merci à ceux qui prendront le temps de m'aider !
-----

[gts2]

Bonjour,

Si je comprends bien vous avez un cylindre central d'axe z et en appui sur ce cylindre un cône ; si oui pour les deux surfaces la normale passe par l'axe Oz, il n' y a donc pas de composantes selon u\theta.
La vue en coupe montre bien N1 dans ce plan {bille, axe Oz}, non ?

Remarque : quel est le cadre de l'étude, parce qu'une bille qui glisse sans tourner dans une rainure ...

[cmole]

Bonjour,

L'image 3D représentant le système n'est pas passée, désolé je vais essayer de corriger ça pour que ce soit plus parlant.

Pour essayer de décrire le système imaginé il s'agit de 2 cylindres concentriques et au bout un plan incliné, pas un cône. On fait circuler une pièce (pastille, pas bille pour éviter le roulement justement !) en lui appliquant une force colinéaire à l'axe des cylindres.

Je ne sais pas si c'est plus clair, dès que possible je remets une vue 3D qui sera sûrement plus parlante, car pour moi les 2 normales ne passent pas uniquement par Z et il y a donc une composante suivant Utheta.

Merci pour ce premier retour !

[gts2]

OK, j'ai mieux compris le schéma.

Le problème, comme vous l'avez détecté, est lié à la constante de N1 et plutôt que d'accuser la relation cinématique qu'il est difficile de mettre en doute (sauf erreur de calcul), il faut plutôt mettre en cause la constante de N1.
D'autant plus que vous avez une autre hypothèse que les conditions initiales non indiquées dans le message initial.
Quels sont vos arguments pour "N1 devrait être constant et ne dépendre que de la force F et de l'angle phi" ?

[A voir en vidéo sur Futura]

[gts2]

Suggestion : s'il n'y a pas de frottement, une méthode énergétique peut s'envisager.

[cmole]

Là où j'ai un peu de mal justement c'est pourquoi N1 ne serait pas constante ?
Si je fais une analogie assez grossière (et c'est peut-être là le problème) avec un simple plan incliné, alors on a N = Fcos(phi). La façon dont je vois la chose, c'est que le système étudié ne serait qu'un simple plan incliné auquel on vient "ajouter" des obstacles pour modifier la trajectoire, ce qui selon moi ne devrait pas influer sur N1.

Voici l'image 3D (il s'agit juste d'un concept pour représentation, il n'y a pas de réel système derrière) :



De base je pensais que mon erreur (s'il s'avère qu'il y en a bien une) venait de la relation entre θ" et z", sur ce point là est-ce correct ? (d'ailleurs il y a une coquille dans la capture 4, il s'agit de z" et non z)

Enfin, pour une méthode énergétique quelle serait la démarche à suivre ? honnêtement je ne me souviens pas être déjà passé par là.

Merci pour votre aide !

[gts2]

N = Fcos(phi) provient du fait qu'il n'y a pas de mouvement perpendiculairement au plan donc somme Fnormale=0.
Ici cela donne (aux erreurs de calcul près) : N1=F cos(phi) + N2 sin(phi) sin(theta) un peu moins simple.

Comme il n'y a pas de frottement on a W(F)=variation d'énergie cinétique, W(F) s'exprime en fonction de z et donc de d'après votre relation cinématique.
L'énergie cinétique s'exprime en fonction de et donc en fonction de
Cela vous donne donc une équation différentielle d'ordre 1 en

[cmole]

Bonjour, avec énormément de retard merci beaucoup pour ces réponses !
En poursuivant mes calculs j'arrive effectivement au même résultat, comme quoi il suffisait de continuer rien de plus...

En revanche j'ai quand même une interrogation : la méthode utilisée ici pour déterminer les constantes N1 et N2 considère que N1 est indépendant de θ pour l'intégration de la formule suivant eθ (méthode de l'esquimau qui glisse sur l'igloo https://myprepa.fr/blog/les-grands-c...s-sup-l-igloo/), ce qui est faux comme vous l'avez expliqué/ça a été "montré" après les calculs. De toute évidence la méthode choisie ici ne convient pas puisqu'on ne peut intégrer l'équation sans connaître le lien entre N1/N2 et θ.

Pour résoudre ce système, y a-t-il une autre démarche à suivre ? honnêtement, excepté remplacer N1 par son expression déduite de la projection suivant z dans l'équation suivant θ je ne vois pas comment faire (ici j'utiliserais un solveur Python, par exemple).

Une méthode énergétique pourrait-elle fonctionner ? Si oui, alors la relation énergétique est-elle la suivante ?
W(F) = F.z = F.R.sin(θ).tan(phi) = 0,5.M.(z'+R².θ'²) ==> F.z = F.R.sin(θ).tan(phi) = 0,5.M.(R.θ'.cos(θ) + R².θ'²)
Cette équation serait là aussi résolue à l'aide d'une résolution approchée.

Encore merci pour l'aide apportée !

[gts2]

Quelques remarques
W=variation de Ec donc vous supposez qu'à z=0, le système est au repos
Vous avez oublié le carré de z'
Vous avez oublié le tan phi dans l'expression de z'

[cmole]

Effectivement pas mal d'étourderies dans ma réponse, merci pour les corrections.

En ce qui concerne la supposition qu'à z = 0 le système est au repos, celle-ci est faite uniquement pour simplifier les calculs puisque je "découvre" cette méthode .

J'ai une dernière question, suite à cette remarque :

Comme il n'y a pas de frottement on a W(F)=variation d'énergie cinétique

S'il y avait des frottements, la relation serait-elle valide en considérant le travail de cette force de frottement ?

[cmole]

Après quelques recherches en parallèle il semblerait que la présence de frottements ne change rien à la relation (excepté sa résolution plus complexe). Un grand merci pour l'aide apportée !

[gts2]

En effet les frottements ne changent rien : le théorème découle simplement de l'intégration du principe fondamental de la dynamique mais la présence de frottements rend le théorème moins utile :
sans frottement une simple étude cinématique suffit, donc il y a bien simplification ; si on doit utiliser les forces de contact, il faut d'abord calculer celles-ci donc faire l'étude dynamique ce qui limite l'intérêt.