Colebrook formule approchée
Discussions similaires
-
Par mehdi_128 dans le forum Mathématiques du supérieur
Réponses: 31
Dernier message: 18/08/2018, 18h12
-
Par invite884742e6 dans le forum Mathématiques du supérieur
Réponses: 4
Dernier message: 18/01/2016, 10h54
-
Par inviteecaf79e1 dans le forum Programmation et langages, Algorithmique
Réponses: 0
Dernier message: 11/02/2013, 19h29
-
Par invite7d47809b dans le forum Mathématiques du collège et du lycée
Réponses: 4
Dernier message: 27/12/2012, 11h24
-
Par invite4cada53c dans le forum Physique
Réponses: 3
Dernier message: 04/04/2012, 17h31




 avec a le coeff. numérique et k le log.
avec a le coeff. numérique et k le log.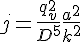 ?
?