Equation dynamique en rotation (couplage mecanique/magnétique)

[gogo218]

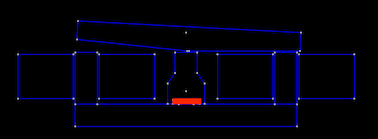
Bonjour,

Je sollicite votre aide sur ce forum scientifique dans le cadre d'une étude de système. Mon objectif est de modéliser ce système sous forme d'équations dynamiques afin de déterminer la fonction de la vitesse de rotation en fonction du temps, et surement de l'angle de rotation.

Le levier magnétique, situé en haut de l'image, est bloqué en position -3° contre un noyau magnétique de section rectangulaire grâce à un aimant placé au centre inférieur du système. L'objectif est de faire basculer ce levier magnétique de -3° à 3° en compensant le couple magnétique de l'aimant par un couple électromagnétique induit par une bobine enroulée autour des parties droite et gauche du noyau magnétique.

J'ai donc tenté d'utiliser le principe fondamental de la dynamique d'un objet en rotation. La matrice d'inertie ne pose pas de problème; en revanche, l'expression des couples en fonction du courant i(t) est plus complexe. Ce courant varie forcément dans le temps en raison de la décharge progressive de la bobine, à mesure que l'entrefer entre le levier magnétique et le noyau augmente.

Il est évident que la perméabilité magnétique des matériaux, les champs magnétiques, le nombre de spires, la longueur du solénoïde et la surface entrent en jeu. Je vous demande donc de l'aide pour trouver l'expression des deux couples qui s'opposent dans ce système. N'hesitez pas à proposer d'autres moyens de résolutions

Merci d’avance,


-----

[gts2]

Bonjour,

On doit pouvoir calculer à la main mais connaissez-vous femm : https://www.femm.info/wiki/HomePage?

Si vous ne connaissez pas, il faut un temps non négligeable pour l'apprivoiser, il faudrait donc savoir si le jeu en vaut la chandelle.

Le dessin n'est pas complet ? Parce que symétrique ?

[gts2]

Remarque : je ne comprends pas bien votre dispositif : où est l'axe de rotation ?
Si on pouvait avoir le schéma complet...

[yaadno]

bjr:
D"après ce que je comprends,l'axe du levier se trouve en haut à droite;ça ressemble à un casse noix,la noix étant l'aimant central;
Les bobines doivent exercer une force variable capable de décoller l'aimant,puis de le ramener à l'angle recherché;?
cdlt

[A voir en vidéo sur Futura]

[gogo218]

Bonjour,

Merci pour votre reponse. Voila le schema complet (je ne l'avais pas montré dans son intégralité car il est symetrique)

[gogo218]

Bonjour,

Je vous remercie pour votre réponse. Femm est il un logiciel de FEM? Si oui, le schema envoyé est issu d'un logiciel de FEM où le systeme est deja modélisé.
Je vais jeter un coup d'oeil dans tous les cas. Oui en effet il est symétrique

[gogo218]

Oui le rôle des bobines est de contrer le couple magnétique. j'ai du coup beaucoup de mal à trouver une expression adapté pour le couple induit par l'enroulement. j'ai cette expression la : T=k⋅Φ⋅i avec i le courant et Φ le flux mais pour l'expression de i(t) j'obtiens l'expression qui résulte de la résolution de l'équation différentielle d'un circuit RL, mais cela ne dépend pas de l'entrefer qui se crée lorsque le levier se détache.

Pour ce qui est du couple magnétique, je pensais calculer T= F x r , r étant le bras de levier et F la force magnétique.

[gts2]

Si votre schéma est déjà dans un logiciel, demandez au logiciel de faire les calculs.
Sinon, à la main, cherchez B à l'aide du circuit magnétique, quelque chose du genre :

Re1 et Re2 sont les réluctances des deux entrefers dépendant de l'angle.
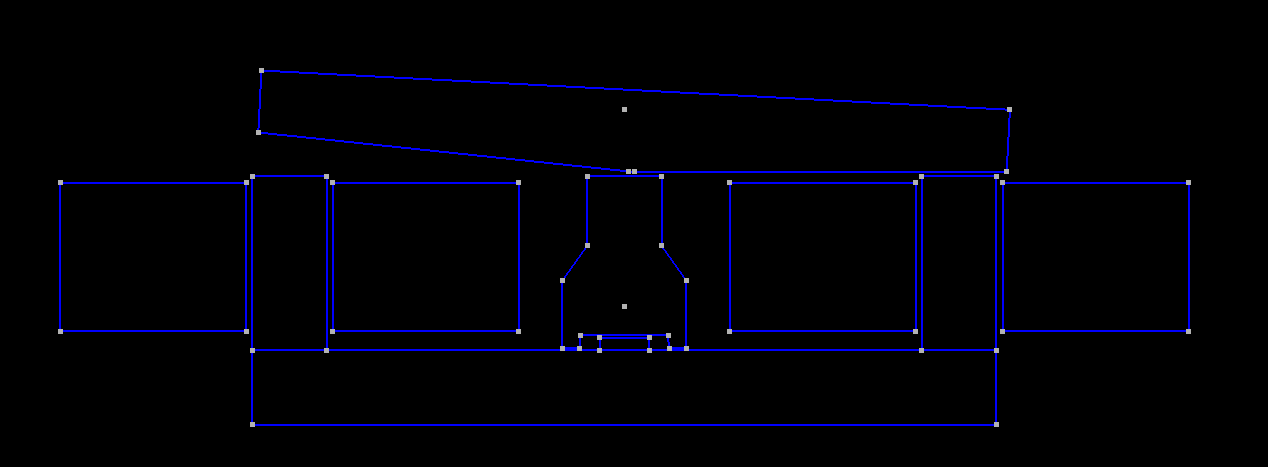
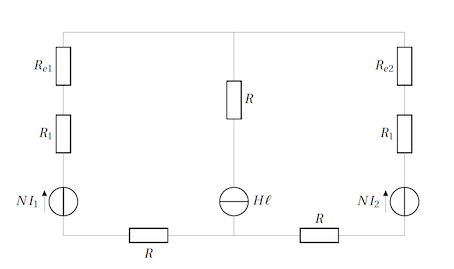
Et à partir de B déterminer les deux forces au niveau des entrefers.

[gts2]

pour l'expression de i(t) j'obtiens l'expression qui résulte de la résolution de l'équation différentielle d'un circuit RL, mais cela ne dépend pas de l'entrefer qui se crée lorsque le levier se détache.

Si par l'intermédiaire de L qui dépend de l'entrefer.

[gogo218]

Étant donné que le logiciel utilisé, Gmsh, ainsi que le modèle ont été créés par l'Université de Liège, il n'y a pas de fonction intégrée permettant d'obtenir directement ce que je souhaite. En effet, le script .pro me permet seulement de représenter le couple magnétique et les flux en fonction du courant, de l'angle de rotation, etc. Cependant, je viens de penser que je pourrais, à partir du tracé du couple, utiliser MATLAB pour écrire un code permettant d'interpoler l'expression de la fonction.

Quoi qu'il en soit, ma mission est de corréler les résultats numériques avec ceux obtenus manuellement.

[gts2]

Quoi qu'il en soit, ma mission est de corréler les résultats numériques avec ceux obtenus manuellement.

Donc message #8.

[gogo218]

Oui je pense qu'une approche de ce genre est le mieux à faire.
J'imagine que NI est le produit du nombre de spire et du courant?
cependant je ne comprend pas trop la presence des deux R ainsi que le Hl ? H correspondant a l'excitation?

Je vous remercie pour votre implication c'est tres gentil

[gts2]

Bonjour,

cf. théorème d'Hopkinson et la notion de réluctance que vous connaissez, je suppose.

On écrit le théorème d'Ampère sur les deux mailles :
, on transforme par Hopkinson en RΦ, avec les R du bas celles de la barre du bas, R1 celle du noyau des bobines, Re1 celle de l'entrefer, R' noyau central, je viens de voir que j'ai oublié la barre du haut disons R'' et on obtient

Après tout dépend comment vous approximer l'aimant, si on linéarise, on peut écrire H=-H0+k(Φ1+Φ2) (H0 donne le générateur de courant) ce qui donne deux équations en Φ1 et Φ2 de paramètres les courants et l'épaisseur de l'entrefer par l'intermédiaire de Re1 Re2.

N est bien le nombre de spires, I le courant.

[gogo218]

Oui ces theoreme m'est familier mais sous la forme integrale de B.dl = mu0.I mais je comprend le passage à H.dl = NI
Je sais egalement grace a la loi d'hopkinson que phi.R est homogène à une force magnétomotrice. Cependant c'est la passerelle entre la loi d'hopkinson et le theoreme d'ampere qui est assez flou pour moi. Et j'imagine que vous l'avez appliqué a une seule maille?

[gts2]

Oui ces theoreme m'est familier mais sous la forme integrale de B.dl = mu0.I mais je comprend le passage à H.dl = NI

Dans le vide, le théorème d'Ampère s'écrit bien , mais dans le cas général, il s'écrit

Je sais egalement grace a la loi d'hopkinson que phi.R est homogène à une force magnétomotrice. Cependant c'est la passerelle entre la loi d'hopkinson et le theoreme d'ampere qui est assez flou pour moi.

Voir par ex. Nicolas Rosee

Et j'imagine que vous l'avez appliqué a une seule maille?

Oui, les deux étant symétriques (à l'entrefer près), il suffit de changer les indices.

[gogo218]

d'accord, je saisi beaucoup mieux.
J'ai commencé la chose suivante :

Je peux donc l'appliquer a toutes mes reluctances dans la boucle, lorsque vous dites que j'essaye de trouver le champs, j'imagine qu'il faut que je remplace le flux par le produit du champs et de la surface et ue j'isole ce dernier c'est bein ca ?

[gts2]

C'est correct : R'' doit être dans les deux branches comme le R du bas.

Une fois que vous aurez Φ1 et Φ2, vous calculerez B1 et B2 dans les deux entrefers puis les forces et en prime vous aurez L1=Φ1/Ι1.

[gogo218]

Ok ca marche pour le R'' . J'ai déterminé mes longueur de la maniere suivante: IMG_5494.jpg
de telle maniere à avoir ces expressions pour chaque reluctances: IMG_5495.jpg
J'ai tout remplacé dans l'equation et j'obtient ca.
Je m'excuse si je vous fait répéter mais cela n'est toujour pas clair pour moi concernant la determination du champs. dois-je isoler Phi1 et identifier B1? et qu'en est il de B2? car si j'isole B1 il sera tout de meme dépendant de B2. et une fois trouvée je dois l'inserer dans la formule de la force B^2.S/2muo mais pour moi cette force s'applique au niveau du noyau. Comment l'exprimer aux niveaux des entrefers comme vous le suggérez?

[gogo218]

ou alors pour trouver phi1 et 2 je dois résoudre le systeme en posant les equations des deux boucles?

[gts2]

ou alors pour trouver phi1 et 2 je dois résoudre le systeme en posant les equations des deux boucles?

C'est bien cela.

[gogo218]

D'accord merci infiniment ! je vais essayer

[gts2]

Pour moi l et r c'est la même chose.
J'ai l'impression que l'aimant c'est ce que j'ai mis en rouge ?

Problème de vocabulaire : H0 c'est le champ pour un flux nul.
Le S central est le même que celui du noyau des bobines ? En plus ce n'est pas un cylindre. Mais pour commencer on peut faire comme si.

La force B^2.S/2μ0 s'applique là où vous calculez B sur la section correspondante.

[gogo218]

pour moi r c'est le bras de levier du levier magnétique qui est en rotation. les surfaces dans la brache de gauche et de droite ainsi que la branche du bas horizontale sont les memes et j'ai supposé la branche du milieu de section égale sans prendre en compte la variation de section pour simplifier. dans le cas du HL qui caractérise l'aimant, L est le trajet total du flux? je ne comprends pas trop pourquoi l et r sont la meme chose pour vous?
Et lorsque vous dites que H0 est le champs pour un flux nul c'est a dire l'excitation de l'aimant lorsque le courant dans les bobine est nul?

[gts2]

l et r c'est la même chose à la lecture du dessin (longueur en haut = longueur en bas)

Dans HL, L est le trajet dans l'aimant, d'où ma question où est l'aimant ?, qui en général est de forme simple, donc pas tronconique.

Si vous regardez votre formule, vous voyez bien que H=H0 lorsque (Φ1 + Φ2)=0, sur la droite linéarisée B(H), c'est lorsque la droite coupe l'axe des x.

[gogo218]

Oui oui pardon l'aimant est bien ce que vous avez déssiné en rouge.
Ah oui effectivement r et l sont égaux oui, je pensais que vous parliez d'un autre L.

[gts2]

Bonjour,

Je viens de m'apercevoir que j'ai mis un générateur de courant pour HL, c'est en fait un générateur de tension.