Bonjour,
Désolé de vous déranger, je n'y arrive pas, j'aimerais bien que vous m'aidiez s'il vous plaît.
Voici l'énoncé du problème que j'ai à faire :
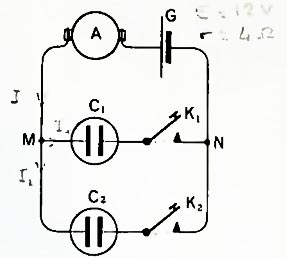
On réalise le réseau à deux nœuds. G est un générateur de f. e. m. E = 12 V et de résistance interne r - 4 0;
A est un ampèremètre de résistance négligeable; G1 et G2 sont deux électrolyseurs montés en parallèle munis chacun d'un interrupteur.
a) On ferme l'interrupteur K1 seul; l'ampèremètre indique 2 A;
b) On ferme l'interrupteur K2 seul; l'ampèremètre indique 1,75 A;
c) On ferme les 2 interrupteurs; l'ampèremètre indique 2,25 A.
Arrivé là, je compte les inconnues : I1, r1 et E1 sur la première boucle, I2, r2 et E2 sur la deuxième. Donc 6.
Avec à ma disposition :
Les équations respectives des 2 boucles quand un seul interrupteur est fermé:
E1 + 2r1 = 4 (c'est à dire U qu'on calcule facilement avec 2A d'intensité) (1)
E2 + 1.75r2 = 5 (pareil, avec I = 1.75) (2)
L'égalité de la ddp aux nœuds quand les deux interrupteurs sont fermés, ce qui donne :
E1 + I1r1 = E2 + I2r2 (3)
La somme des intensités dans les boucles qui me permettrait très vite d'éliminer une inconnue sur les 6.
i1 + i2 = 2.25 (4)
Et encore (qd les 2 interrupteurs sont fermés) la règle 1/r1 + 1/r2 = 1/R
Sachant qu'on connaît U = 12 - (2.25*4) = 3 V. et aussi I, on peut réintégrer 1/R dans I/U = 1/R soit :
2.25 / 3 = 1 / R = 1/r1 + 1/r2 (5)
On demande la valeur de presque toutes les inconnues.
Avec 5 équations pour 6 inconnues, j'ai l'impression que quelque chose m'a échappé. Il y a une règle que je n'ai pas appliquée. Ou alors je me plante complètement. Vous pouvez m'orienter svp ?
Merci !
-----