Bonjour, j'ai un problème de physique à programmer sur SageMaths. L'énoncé de l'exercice est: Des déchets enfouis profondément émettent de la chaleur. Comment cette chaleur se propage-t-elle jusqu'au sol? Afficher le profil de température en fonction de la profondeur pour un temps quelconque.

Pour résoudre ce problème, j'ai utilisé la résolution matricielle mais le profil de température que j'obtiens n'est pas correct. Pourriez-vous m'indiquer si il y a un soucis dans mon programme. Merci par avance.

Code:
# DONNÉES
h = 50                       # Profondeur (m)
S = 7.1*10^6                 # Surface (m²)
tau = 50                     # Temps de désintégration totale des déchets (ans)
L = 1.5                      # Lambda : conductivité thermique (W/K/m)
P0 = 1000                    # Puissance (W)
D = 1.18*10^-6               # Coefficient de diffusion thermique (m²/s)
 
A=(-36000*P0)/(2*L*S)        # A=(-N*P0)/(2*L*s) avec N: nombre de colis
taille=10
T0=[matrix(taille,1,lambda i,j: 25)] # matrice 10 lignes 1 colonne de 25 à t=0 pour tout z    #liste de vecteurs température initial
M=matrix(RR,taille)                  # matrice 10x10 de 0
 
for i in range(taille-1):            # Discrétisation de l'équation de la chaleur
    M[i+1,i]=D
    M[i,i+1]=D
    M[i,i]=1-2*D
M[0,0]=1.0
M[taille-1,taille-1]=1.0
M[0,1]=0.0
M[taille-1,taille-2]=0.0
 
#puissance dissipée en z=0 pour tout t
P=[matrix(RR,taille,1,{(0,0):A*exp(-i/tau)}) for i in range(0,100)]
 
T=T0 #initialisation
for i in range(100):  #itérateur qui va construire les températures
    TT=M*T[i]-P[i]
    T.append(TT)
Code:
graphique=sum([list_plot([(i,(T[10*j][i][0])) for i in srange(taille)],plotjoined=True) for j in srange(10)])
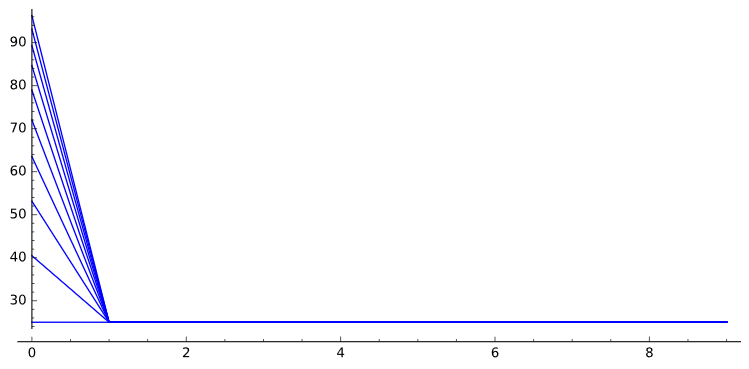
Graphique:
Nom : tmp_CoDAEP.png Affichages : 47 Taille : 18,9 Ko