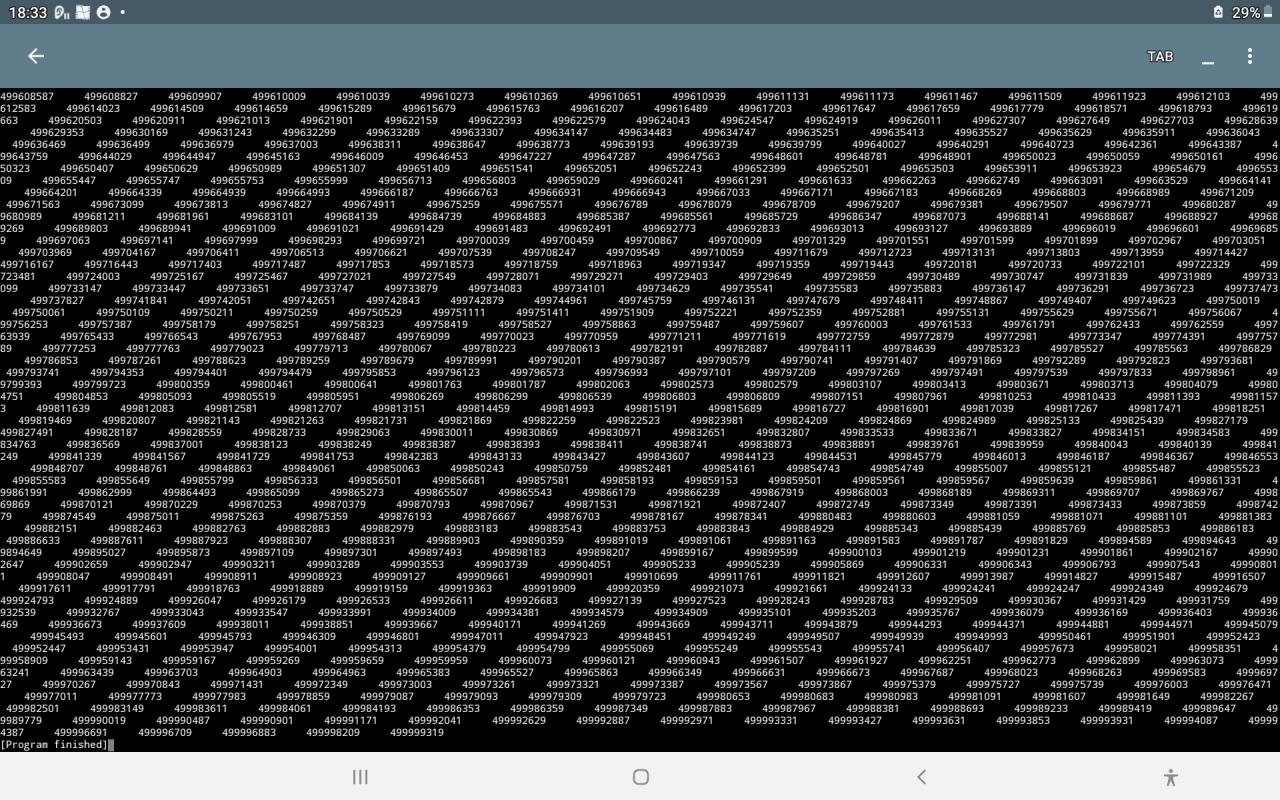
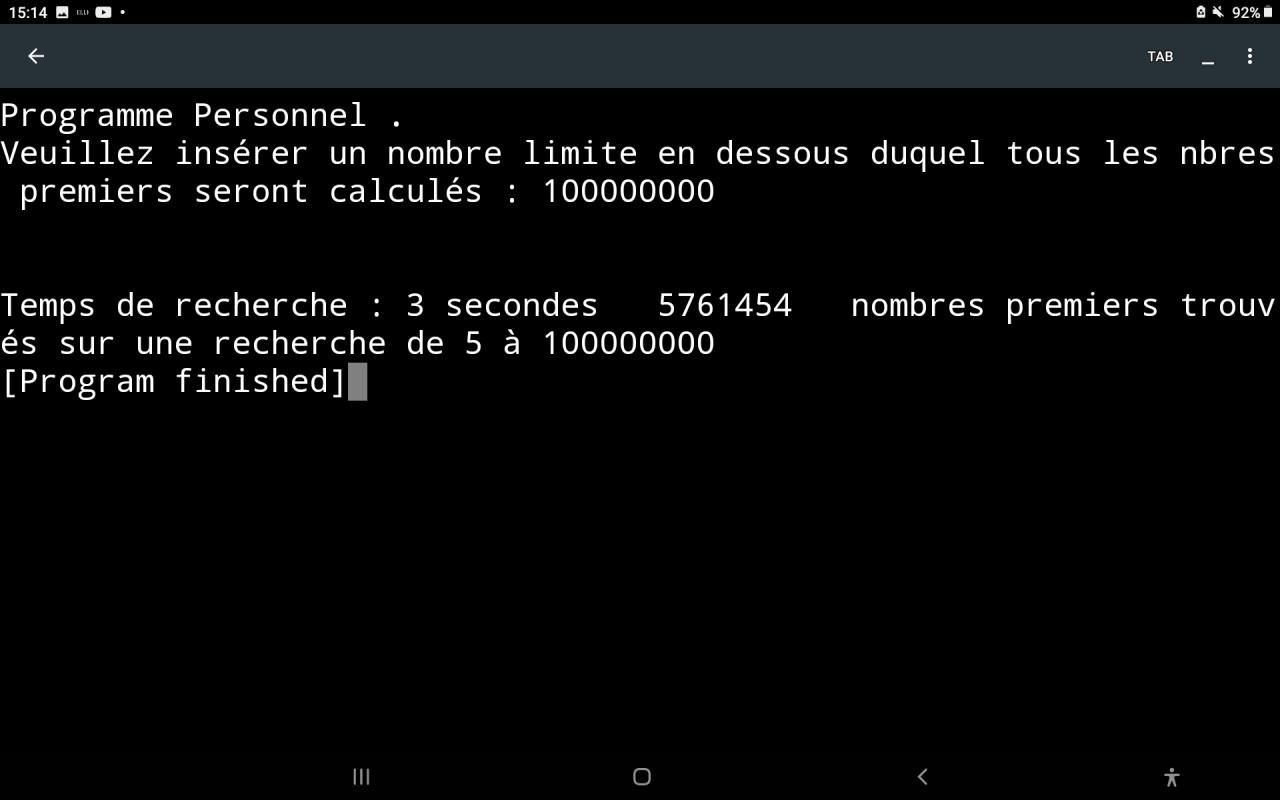
L’ensemble P des nombres premiers est-il l’ensemble des X tel que pour :
a € Z* et
n € Z* on ait
P = { X = | (6a -1)| } + { 2 , 3 } - { Un = X × [ |(6n - 1)| ]}
Avec Un étant une suite arithmétique ?
Cela me semble fonctionner, seule l’utilisation des symboles mathématiques peut vraiment m’echapper
Merci à vous.
Dernière modification par Porte7 ; 12/12/2023 à 14h35.
Salut,
De fait c'est incompréhensible. J'arrive pas à donner du sens à ton expression.Envoyé par Porte7
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
OK
Bonjour Deedee,,
En coupant l’expression en 2
P = { X = | (6a -1)| }
J’ai voulu traduire par là que
Si a prend toutes les valeurs entières entre - l’infini et + l’infini sauf 0 alors l’ensemble des X sera la suite
X = { 5 7 11 13 17 19 23 25 etc etc }
+ 2 et 3 comme nombre premiers qui manquent que j’ai écrit de cette manière
+{ 2 , 3 }
.........
Dernière modification par Porte7 ; 12/12/2023 à 14h58.
Je ne sais pas si c’est plus clair pour cette portion ?
Oui et je n'avais pas compris en effet.
Mais déjà là c'est pas possible. 7 n'est pas de la forme 6a - 1 !!!!
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Je vais préciser avec des exemples :
Si a = 1 alors valeur absolue de (6a -1) =5
Si a = -1 alors valeur absolue de (6a -1) ou de -7 est égale à 7
Si a = 2 => val absolue de (6a - 1) = 11
Si a = -2 => val absolue de (6a - 1) ou |(-13)| = 13
etc etc et ainsi je génère ma suite citée plus haut.
Comme a ne prend pas la valeur 0 on a pas 1 comme nombre premier.
Dernière modification par Porte7 ; 12/12/2023 à 15h34.
Ah la valeur absolue m'avait échappé.
Il serait plus simple sans doute d'écrire 6a-1 et 6a+1.
Mais bon, ok pour cette première partie
(suite avec les autres ou demain, ma journée est finie)
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Avec vous je préfère
A demain donc.
Bonsoir
Bonjour Deedee,
La seconde partie consiste à retirer de l’ensemble comprenant tous les éléments de la première suite { 5,7, 11, 13, 17, 19, 23, 25, 29, 31, 35,....49,...55,...65,...77,.. .85,...91...} tous les multiples de nombres premiers impairs tels que 25 35 49 55 65 77 85 91 etc etc en multipliant chaque élément individuellement par une suite identique à la première avec une
variable n définie aussi sur Z*.
On a donc la suite Un = X × [ |(6n - 1)| ]
Merci.
Salut,
Ca m'a l'air juste. A confirmer.
Bon, ça ne révolutionnera pas les performances. La méthode de prendre les 6a+-1 et d'enlever les multiples ça existe depuis deux mille ans. Que ce soit par un calcul direct des multiples (on a dû tous s'amuser à ça étant gamin dans ce forum
Pour générer non pas tous les nombres premiers mais un grand paquet de nombres premiers, avec des performances fantastiques, les techniques basées sur les nombres de Mersenne et le petit théorème de Fermat peuvent difficilement être battues. On trouve ça un peu partout sur le net.
Pour générer moins de nombre premiers mais des nombres premiers extrêmement grands il existe aussi diverses techniques incroyablement performantes, utilisées en particulier par les outils de cryptographies, mais là je ne connais pas ces techniques (certaines sont probabilistes mais bon, ça, c'est pas ce que tu cherches).
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Salut Deedee,
Je suis bien d’accord.
Rien de révolutionnaire bien entendu.
Sauf pour un vieux croûton comme moi qui est bien content d’arriver à se faire toucher encore 2 neurones
On garde donc l’expression que j’ai écrite ou pas ?
Merci
Elle n'est pas "carrée" point de vue notations mais sinon elle me semble juste, donc tu peux la garder
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
"retourner L" ... l'auteur du fil parlait des nombres premiers plus petits que 10^5. Ca fait un gros gros L. Ce serait mieux à mon avis de ne renvoyer que les nombres premiers (il y en a déjà pas mal).
Merci Deedee, c’est toujours un plaisir avec vous, bye bye
Ayant été en vacance au moment du post original, j'ai commencé à me mettre au défi (pour le fun et mon éducation) de calculer les nombres premiers jusqu’à 1000 milliards sur ma machine (qui possède 80Go de RAM étant dans le domaine de la simulation numérique) le plus rapidement possible tout en restant dans le classique crible d’Ératosthène (je sais qu'il existe mieux mais je voulais y aller par étape).
J'ai donc commencé par gérer le tableau de booléen par un vrai tableau de bits (et non d'octets). Puis j'ai changé mon algo pour ne stocker dans le tableau que les nombres impairs. Ça m'a permis de rentrer les 1000 milliards dans 64 Go de RAM (précisément 625000000 octets). Malgré la surcharge de code (que j'ai passé pas mal de temps à optimiser en regardant le code assembleur généré par mon compilateur Delphi) j'ai pas mal gagné.
Mais je me suis heurté à la mémoire cache, pour en calculer jusqu'à 100 000 000, ça me prend environ 8/100eme de seconde, mais dés que je passe à 1 000 000 000, ça me prend 3s, soit 30 fois plus. Donc le problème est au niveau du cache.
J'ai donc commencé à implémenter une version segmentée pour optimiser la mémoire cache.
Bon, actuellement, j'ai un bug, mais dés que je serai de nouveau en congé, je ne désespère pas d'y retourner et d'y arriver (d'ailleurs d'après ce que j'ai pu lire, avec une bonne gestion du cache, la surcharge de code du à la gestion par bit au lieu d'octet n'est plus forcément intéressante, je veux bien le croire, mais comme j'ai ultra optimisé la gestion par bit, je voudrais en être sûr).
C'est un algo de base pour le crible, pas une implémentation.
Comme dit dans mon message précédent, l'implémentation est largement plus subtile en tenant compte de la mémoire cache et du compilateur.
Pour info, pour obtenir la meilleure performance, il faut que le tableau de résultat soit stockée dans une variable globale pour éviter des indirections de pointeur durant le calcul.
Dernière modification par Garion ; 13/12/2023 à 22h49.
Le programme ci dessous marche mais j’ai un pb de mémoire à priori . Il m’affiche "Segmentation Fault" si j’entre une valeur au dessus de 45001 environ.
Assez simple finalement, c’est une base de travail))
C’est certainement pas performant si ce n’est l’économie en lignes de code!!!
#include stdio.h //tous les fichiers .h à mettre entre
#include stdlib.h // chevrons ouvert fermés
#include conio.h
int main(int argc, char *argv[])
{
int x;
printf(" Nombres premiers entre [5....x[ , entrez une valeur pour x : ");
scanf(" %d", &x);
int T[x];
for(int i=6; i<=x; i = i+6)
{
for(int j = i -1 ; (i-1)*j<=x; j = j+6)
{
T[(i-1)*j] = 1;
if ( (i+1)*j <= x )
{
T[(i+1)*j] = 1;
}
}
for(int j = i+1 ; (i-1)*j<=x; j = j+6)
{
T[(i-1)*j] = 1 ;
if ( (i+1)*j <= x )
{
T[(i+1)*j] = 1;
}
}
}
for(int i=6; i<=x; i = i+6)
{
if (T[i-1]== 0) {printf("\n % d est premier", i-1);}
if (T[i+1]== 0) {printf("\n %d est premier", i+1);}
}}
Dernière modification par Porte7 ; 23/12/2023 à 17h46.
1) il faudrait apprendre à utiliser les balises CODE.
2) le segmentation fault vient sans doute de l'allocation d'un tableau dynamique sur la pile. Un malloc devrait régler le problème.
Et surtout apprendre à indenter le code (j’avais vérifié : il ne l’est pas, sinon j’aurais ajouté la balise), ce qui est du niveau de maternelle dans l’apprentissage de la programmation.
Rien ne sert de penser, il faut réfléchir avant - Pierre Dac
Pour l’indentation du code un cop-col m’à remis tout à la ligne.
On va voir avec le malloc.
Il fut un temps où j’avais de bien meilleures bases.....rassurez vous.
Code:#include <stdio.h> #include <stdlib.h> #include <conio.h> int main(int argc, char *argv[]) { int x; printf(" Nombres premiers entre [5....x[ , entrez une valeur pour x : "); scanf(" %d", &x); int T[x]; for(int i=6; i<=x; i = i+6) { for(int j = i -1 ; (i-1)*j<=x; j = j+6) { T[(i-1)*j] = 1; if ( (i+1)*j <= x ) { T[(i+1)*j] = 1; } } for(int j = i+1 ; (i-1)*j<=x; j = j+6) { T[(i-1)*j] = 1 ; if ( (i+1)*j <= x ) { T[(i+1)*j] = 1; } } } for(int i=6; i<=x; i = i+6) { if (T[i-1]== 0) {printf("\n % d est premier", i-1);} if (T[i+1]== 0) {printf("\n %d est premier", i+1);} } }
Dernière modification par Jack ; 23/12/2023 à 20h26. Motif: Ajout balises code
Toujours le même problème!
Tant pis le malloc c’est une bonne idée.
Bonjour Deedee et merci pour votre aide cela m’a permis de minimiser le nombre de ligne de code.
Bonnes fêtes de fin d’année.
Code:#include <stdio.h> #include <stdlib.h> #include <new> int main(int argc, char *argv[]) { int x,val; printf(" Nombres premiers entre [5....x[ , entrez une valeur pour x "); scanf("%d", &val); bool * Tableau = new bool [val]; x = val/6; x = 6*x; printf("\n\n\n"); for(int i = -x; i<=val; i= i+6 ) { for(int j = abs(i -1) ; (i < 0 && (i+1)*j >= -val ) || (i>0 && (i-1)*j <= val); j = j+6) { Tableau[abs((i-1)*j)] =Tableau[abs((i+1)*j)] = 1; } } for(int i = -x; i<=val; i= i+6 ) { if (abs(i-1)!= 1 && Tableau[abs((i-1))]== 0) { printf(" % d ",abs(i-1) ); } } }
Dernière modification par Porte7 ; 24/12/2023 à 22h38.
Après un bug rectifié j’ai plus eu de pb d’overflow memoire.
Le new m’a servi le malloc aurait pu faire aussi bien.
Mais j’avais des affectations en dehors de T[val] que j’ai rectifié par des tests d’affectation supplémentaires
Merci à vous tous et à ma petite tablette.
Dernière modification par Porte7 ; 26/12/2023 à 07h37.
Screenshot_20240111-184515_Gallery.jpg
Screenshot_20240111-183521.jpg
Bonjour,
Je ne sais pas trop quoi en penser!!!
En haut les résultats du crible d’Atkin
En bas les performances que je sors sur ma tablette.
Moi non plus mais c'est juste que comme tu as eu la flemme de recopier 2 ou 3 chiffres et que tu postes des copies d'écrans peu lisibles avec même un clavier dedans en supposant qu'on est là pour faire l'effort à ta place, j'ai eu la flemme aussi.
Bonjour,
Pourriez- vous me confirmer qu’il s’agit ici d’un programme de recherche des nombres premiers Atkin?
Merci!
Code:#include <stdio.h> #include <stdlib.h> #include <conio.h> #include <math.h> #include <time.h> #include <new> int main ( ) { int comptageNP =0; int limite ; int wlimit ; int z ; printf ( "Programme Atkin . \nVeuillez insérer un nombre limite en dessous duquel tous les nbres premiers seront calculés : " ) ; scanf ( "%d" , & limite ) ; time_t debut = time(NULL); bool * sieb = new bool [limite]; wlimit = sqrt ( limite ) ; for ( int x = 1 ; x <= wlimit ; x++) { for ( int y = 1 ; y <= wlimit ; y++ ) { z = 4 * x * x + y * y ; if ( z <= limite && ( z % 60 == 1 || z % 60 == 13 || z % 60 == 17 || z % 60 == 29 || z % 60 == 37 || z % 60 == 41 || z % 60 == 49 || z % 60 == 53 ) ) { sieb [ z ] = ! sieb [ z ] ; } z = 3 * x * x + y * y ; if ( z <= limite && ( z % 60 == 7 || z % 60 == 19 || z % 60 == 31 || z % 60 == 43 ) ) { sieb [ z ] = ! sieb [ z ] ; } z = 3 * x * x - y * y ; if ( x > y && z <= limite && ( z % 60 == 11 || z % 60 == 23 || z % 60 == 47 || z % 60 == 59 ) ) { sieb [ z ] = ! sieb [ z ] ; } } } for ( int je = 5 ; je <= wlimit ; je++ ) { if ( sieb [ je ] == 1 ) { for (int j = 1 ; j * je * je <= limite ;j++ ) { sieb [ j * je * je ] = 0 ; } } } for ( int je = 5 ; je <= limite ;je++) { if ( sieb [ je ] == 1 ) { comptageNP++; } } time_t fin = time(NULL); printf ("\nTemps de recherche : %d secondes %d nombres premiers trouvés sur une recherche de 5 à %d", fin- debut,comptageNP,limite); }
Dernière modification par Porte7 ; 12/01/2024 à 15h57.
Bonjour,
J’avais la flemme de rester couché ce matin.
Bonne journée.
