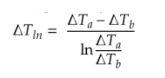Bonjour à tous,
Dans le cadre d'une rénovation énergétique d'un bâtiment tertiaire, le système de production de chauffage est remplacé. Actuelle il est assuré par une chaudière gaz à condensation qui alimente un réseau de radiateur et des batteries à eau chaude de CTA (centrale de traitement d'air) en 65/45 °C. Le nouveau système est une PAC géothermie qui va alimenter les batteries à eau chaude des CTA en 50/30 °C.
Je souhaite donc connaitre la nouvelle puissance de mes batteries après ce changement de régime d'eau. En CVC (Chauffage Ventilation Climatisation) pour connaitre la puissance disponible dans les systèmes nous appliquons la formule : P[kW]=1,16xqv[m3/h]xΔT. Dans les deux cas, le ΔT entre la température d'entrée et de sortie de la batterie est identique (20°C) et notre débit (qv) inchangé. Ce qui par principe ne modifie pas la puissance disponible dans la batterie. Mais ma batterie à eau chaude est un échangeur eau/air. Sa fonction est de réchauffer l'air de la CTA avec de l'eau chaude avant de la souffler dans le bâtiment. Baisser la température du fluide chaud doit entrainer logiquement une baisse de la chaleur échangée entre l'eau et l'air. Donc une baisse de la puissance de la batterie et une baisse de la température de l'air soufflé.
En fouillant mes cours d'échangeurs thermiques j'ai trouvé cette relation : P = ΔT_ln/R_global
Avec mes données initiales, je peux calculer ΔTln (contre courant) et donc déterminer le R_global qui va être constant.
avec ΔTa : T_entrée de l'eau - T_sortie de l'air et ΔTb : T_sortie de l'eau - T_entrée de l'air.
Avec les nouvelles températures, je calcule ΔT_ln2 puis avec R_global étant une constante je peux déterminer la nouvelle puissance.
Mes données : T_eau entée = 65°C, T_eau sortie 45°C, débit d'eau = 0,412 m3/h, T_air entée = 10,9°C, T_air sortie = 19°C, débit d'air 3 495 m3/h, P_batterie = 9,6 kW
ΔTln = 39,75
R_global = 39,75/9,6=4,16
ΔTln2 = 24,57
P_batterie2 = 5,91 kW
Je voudrais savoir si ma démarche est correcte ?
Enfin pour développer sur la pertinence de ce changement de température, les fabricants (qui sont aussi des vendeurs) conseillent de changer de batterie pour utiliser des batteries adaptées au nouveau régime d'eau. Financièrement ce n'est pas souhaitable, pour regagner la puissance perdue nous avons la possibilité d'augmenter le débit d'eau chaude dans les batteries mais est-ce vraiment pertinent ? On se retrouve avec une augmentation des pertes de charges et donc une augmentation de la consommation d'électricité du circulateur et avec un fluide qui passe plus rapidement, arrive ton vraiment à réaliser un échange efficace ?
J'ai donc tout de même voulu calculer un nouveau débit pour retrouver ma puissance initiale. J'ai pour cela lié deux formules :
- P = ΔT_ln/R_global
- P=1,16 x qv x ΔT
donc : qv = ΔT_ln2/(R_global x 1,16 x ΔT) = 0,255 m3/h
Je me retrouve avec un débit plus faible qu'initialement...
Je doute de la pertinence d'utiliser P=1,16 x qv x ΔT, il me faudrait une relation qui utilise ΔTln et les débits des fluides de mon échangeur. Avez-vous connaissance d'une relation qui va dans ce sens ? Je n'ai rien trouvé de mon coté.
-----