Question sur les trous noirs

[invite6c093f92]

Oui bien sur .

Merci.

C'est à dire lorsqu'un photon arrive au niveau de l'horizon d'un TN, il s'arrête.

C'est quoi un photon qui s'arrete??
Cordialement,
-----

[Zefram Cochrane]

Les photons sont des particules de masse nulle. Leur vitesse de propagation est strictement égale à la vitesse de la lumière qui est plus généralement à la célérité des particules de masse nulle du vide.
SI la vitesse de la lumière instantanée diminue au fur et à mesure que l'on s'approche d'un TN jusqu'à s'annuler au niveau de l'horizon, alors, la photons qui correspond à celle de la lumière devient nulle au niveau de l'horizon, il s'arrêtent donc.

Cordialement,
Zefram

[invite23876543123]

Zefram, je ne dois pas te manquer de respect mais le photon ne s'arrête pas il (son image rougit) mais comment cela est possible, puisque le photon (même avec les téléscopes modernes) c'est ce qui nous permet de voir ??????

[invite6c093f92]

Les photons sont des particules de masse nulle. Leur vitesse de propagation est strictement égale à la vitesse de la lumière qui est plus généralement à la célérité des particules de masse nulle du vide.
SI la vitesse de la lumière instantanée diminue au fur et à mesure que l'on s'approche d'un TN jusqu'à s'annuler au niveau de l'horizon, alors, la photons qui correspond à celle de la lumière devient nulle au niveau de l'horizon, il s'arrêtent donc.

Cordialement,
Zefram

Tu parles bien d'un photon vu par un observateur à l'00?
Alors non, remarque ça doit etre impréssionant un photon qui s'arréte...quel freins!
Je ne vois toujours pas ce qu'est un photon qui s'arrete, désolé.On peut parler de son redshift, mais c'est pas un arret, alors de quoi parles-tu?
Cordialement,
EDIT croisement avec FTD

[invite6c093f92]

mais comment cela est possible, puisque le photon (même avec les téléscopes modernes) c'est ce qui nous permet de voir ??????

Le photon , suivant divers paramètres, redshifterais plus ou moins rapidement(plutot TRES TRES rapidement).Donc pas d'images fossiles.
Cordialement,

[invite23876543123]

Le photon , suivant divers paramètres, redshifterais plus ou moins rapidement(plutot TRES TRES rapidement).Donc pas d'images fossiles.
Cordialement,

Ce que je voulais dire c'est que l'on ne parle pas de photon perçus mais d'une extrapolation de redshift ! Sinon les photons se dédoubleraient sur l'horizon un perçu un traversant l'horizon ?

[Zefram Cochrane]

Un photon, c'est effectivement ce qui nous permet de voir, il n'a donc pas d'image puisqu'il est l'image.

En RG, la vitesse de la lumière coordonnée au niveau de l'horizon du TN est nulle mais localement sa vitesse est constante et égale à C, un observateur quelconque situé à distance aura l'impression qu'un photon émis depuis la surface du TN ne décolle pas. Localement, il a une distance infinie à franchir pour espérer franchir du point de vue d'un observateur un micromètre.
D'où l'utilité de savoir que si Rs est le rayon du TN pour l'observateur à l'oo , quel est le rayon de ce TN pour l'observateur local.

Dans mon idée le photon ne freine pas mais se déplace à une vitesse de la lumière instantannée variable. Prenons l'exemple d'un signal allant de 150 000 000km de l'autre coté du Soleil vers la Terre et rasant le soleil ; on néglige le champs de gravitation de la Terre l'exemple. Première partie du voyage 150 000 000 Km - Soleil. La vitesse du photon au départ est de c et diminue parce que la célérité de la lumière du vide diminue. Seconde partie du voyage après avoir atteint un minimum c' en passant au plus près du Soleil, la vitesse du photon augmente, pas parce qu'il est accéléré, mais parce que sa vitesse de propagation augmente et il atteint la Terre avec une vitesse c. Morale de l'histoire la vitesse moyenne du photon sur l'ensemble du parcourt est inférieure à c (c'est l'effet Shapiro).

Cordialement,
Zefram

[Gilgamesh]

Zefram, on arrête avec les théories perso, merci.

[invitebd9ed9fb]

Oui, bien sûr, il y a suffisamment de temps que je suis sur ce forum pour me rendre compte de ces notions qui sont courantes dés lors qu'on traite de la RG. Ce n'est pas pour autant que j'arrive à les conceptualiser. La notion d'étoile gelée, de mon point de vue, est suspecte (je ne donne ici que mon sentiment personnel sans prétendre avoir raison) pour une raison bien simple : pour un observateur distant, le temps s'arrête au niveau de l'horizon. Que le temps soit relatif, c'est évident, c'est prouvé. De là à admettre qu'il puisse s'arrêter complètement, c'est autre chose, car il s'agit bien là d'une singularité. Et ce qui caractérise une singularité, c'est l'apparition d'infinis mathématiques. La physique est étroitement liée aux maths mais l'infini n'a de sens qu'en mathématique et ne peut représenter une réalité physique. C'est un peu comme l'instant zéro du big bang, l'Univers avant le temps de Planck : ça n'a pas de sens d'en parler.

Bonjour Papy ^^

Si l'idée d'un temps arrêté sur l'horizon du TN te perturbe, il suffit de rappeler l'idée de base de l'étoile gelée pour résoudre le problème:
Vu de loin, l'étoile en effondrement n'atteint jamais l'état final TN. La formation de l'horizon est rejeté, pour l'observateur lointain, dans un futur infini. Une singularité dont l'existence est située dans notre futur n'existe pas réellement pour nous dans notre temps présent. Voilà comment on evite la singularité.
Vu de prés, on tombe dans le TN et le temps local est perçu normalement.

Je rajouterai qu'on peut considérer une étoile gélée comme un "presque trou noir", et que par conséquent le temps à la limite de l'horizon est "presque" arrété, mais pas complétement car le TN n'est pas formé.

Que deux observateurs voient différemment le même phénomène est une chose. De là à qualifier les deux observations de réelles, c'est une notion que je ne parviens pas à admettre, d'autant plus que dans le cas de l'étoile gelée, on n'observera jamais rien. De plus, si on creuse un peu, on se rend compte des difficultés résultant de l'acceptation de cette notion. Par exemple, comment un TN pourrait il être en rotation si le temps y est à l'arrêt ? Or, il se fait que nos moyens techniques nous permettent concrètement de mesurer son moment cinétique. C'est contradictoire, non ?

Dans le cas des trous noirs en rotation, l'espace lui même autour du TN est entrainé par la rotation. Ce calcul colle (littéralement ) avec l'idée d'un temps figé sur l'horizon. Donc ce n'est pas contradictoire

[invite23876543123]

Ce que je voulais dire c'est que l'on ne parle pas de photon perçus mais d'une extrapolation de redshift ! Sinon les photons se dédoubleraient sur l'horizon un perçu un traversant l'horizon ?

Un schéma vaut mieux que mille mots :



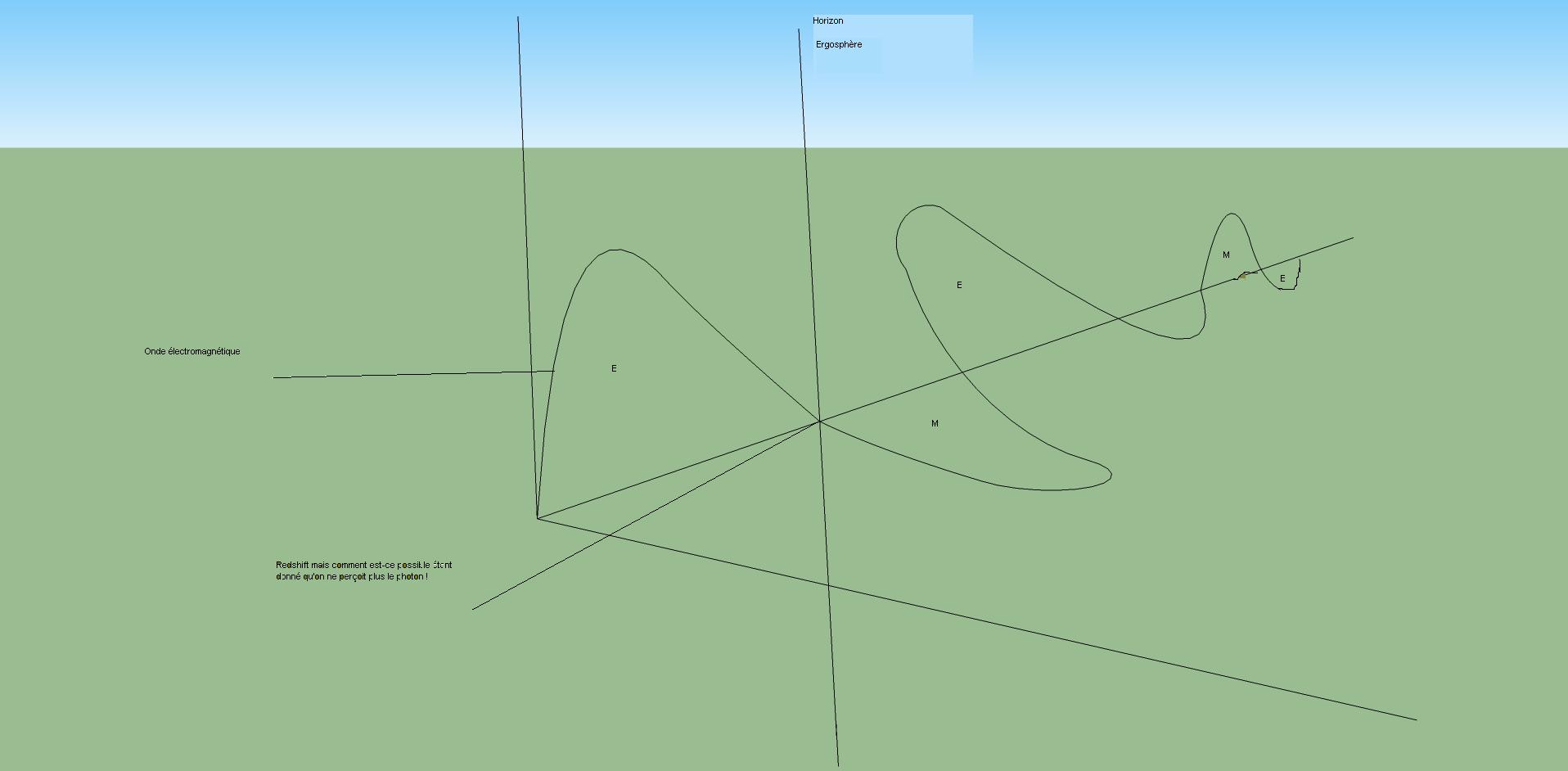
Voici j'expliquerait mon schéma si vous ne comprenez pas !

[invitebd9ed9fb]

Bonjour,

Le temps ne s'arrete pas, jamais, et nulle part.
Cordialement,

bonjour,

on calcul facilement le décalage temporel affectant les satellites. Peut on faire le même calcul pour un objet situé prés de l'horizon d'un TN ? Imaginons qu'un voyageur doté d'une technologie extrêmement avancée parvienne à se maintenir près de l'horizon d'un TN ultramassif (histoire de ne pas être déchiqueté par un effet de marée), tout en conservant la possibilité de faire marche arrière. Quel serait le ralentissement temporel qui affecterait ce voyageur stationnaire par rapport à l'observateur éloigné ?

[papy-alain]

Ce qui me heurte avec la RG, ce sont justement ces différences de "vu de près" et "vu de loin". Je reprends un exemple beaucoup plus simple que le TN. Quand on voit qu'une étoile n'est plus à sa place habituelle lorsque le trajet du rayonnement qu'elle émet passe près du Soleil, on admettra que ce trajet est momentanément modifié, et que quelques heures plus tard cet inconvénient n'existera plus. Si par contre j'utilise la même logique conceptuelle que celle utilisée pour définir le concept du TN gelé, je dirai que l'étoile observée près du Soleil a momentanément changé de place, ce qui est complètement ridicule. Dans le même ordre d'idée, lorsque l'image d'une galaxie lointaine nous parvient fortement agrandie par un effet de lentille gravitationnelle, et qu'après on dresse une carte de l'univers en 3D, va-t-on la représenter telle qu'on la voit, avec une taille démesurée, ou va-t-on rectifier le tir en calculant sa taille réelle ? Dans ces exemples, pourtant issus de la RG, il n'existe qu'une réalité.

[invite6c093f92]

Bonjour,

bonjour,

on calcul facilement le décalage temporel affectant les satellites. Peut on faire le même calcul pour un objet situé prés de l'horizon d'un TN ? Imaginons qu'un voyageur doté d'une technologie extrêmement avancée parvienne à se maintenir près de l'horizon d'un TN ultramassif (histoire de ne pas être déchiqueté par un effet de marée), tout en conservant la possibilité de faire marche arrière. Quel serait le ralentissement temporel qui affecterait ce voyageur stationnaire par rapport à l'observateur éloigné ?

Est-ce pour autant que le temps s'arrete?
Si le temps s'arrete, pendant combien de temps?
La mesure d'intervalle entre deux évenements(durée) n'est pas le temps il me semble.
Corddialement,

[invite6c093f92]

Voici j'expliquerait mon schéma si vous ne comprenez pas !

T'es pas gentil avec nos yeux

[invite23876543123]

T'es pas gentil avec nos yeux

Si tu n'arrives pas à lire fait clic droit sur l'image et "afficher l'image" !

@ +

[Mailou75]

Salut Papy,

Je crois que tu te trompes quand tu parles de réalité : dans le cas d'une lentille gravitationnelle, le rayon lumineux trace une courbe à proximité de la masse.
Supposons qu'on ait deux images, alors toi observateur tu verras deux directions qui sont les tangentes aux courbes au droit de ton œil.
Mais aucune n'est plus réelle que l'autre, l'objet se trouve effectivement au bout de chacune des géodésiques et pour t'y rendre tu peux prendre les deux chemins en ligne droite

Sinon un petit schéma en passant...
Il pose une question : que devient la matière quand elle "tombe" dans un trou noir ?

[invite6c093f92]

bonjour,

on calcul facilement le décalage temporel affectant les satellites. Peut on faire le même calcul pour un objet situé prés de l'horizon d'un TN ? Imaginons qu'un voyageur doté d'une technologie extrêmement avancée parvienne à se maintenir près de l'horizon d'un TN ultramassif (histoire de ne pas être déchiqueté par un effet de marée), tout en conservant la possibilité de faire marche arrière. Quel serait le ralentissement temporel qui affecterait ce voyageur stationnaire par rapport à l'observateur éloigné ?

Puisque c'est sécurisé, je suis le voyageur.
J'ai une énorme montre pour que l'observateur y fasse une lecture aisée.Plus je m'approche de l'horizon et plus il voit la petite aiguille ralentir.En fait la lumière lui parvenant sera tellement redshifté qu'il verra l'image s'assombrire au prorata de la distance me séparant de l'horizon, la longueur d'onde s'allongeant de façon exponentielle.Je suis bien incapable de faire le calcul, mon a-priori est que je serais invisible bien avant qu'il puisse voir la petite aiguille immobilée(temps-coordonnées nul).Si quelqu'un pouvait confirmer ou infirmer.Mais pour mon temps, pas de changement.Bref, le temps ne s'arrete pas.
Cordialement,

[invite6c093f92]

Si tu n'arrives pas à lire fait clic droit sur l'image et "afficher l'image" !

@ +

L'image est affichée....c'est juste ce que tu a noté dessus qui est tout tout tout petit.

[invitebd9ed9fb]

Ce qui me heurte avec la RG, ce sont justement ces différences de "vu de près" et "vu de loin". Je reprends un exemple beaucoup plus simple que le TN. Quand on voit qu'une étoile n'est plus à sa place habituelle lorsque le trajet du rayonnement qu'elle émet passe près du Soleil, on admettra que ce trajet est momentanément modifié, et que quelques heures plus tard cet inconvénient n'existera plus. Si par contre j'utilise la même logique conceptuelle que celle utilisée pour définir le concept du TN gelé, je dirai que l'étoile observée près du Soleil a momentanément changé de place, ce qui est complètement ridicule. Dans le même ordre d'idée, lorsque l'image d'une galaxie lointaine nous parvient fortement agrandie par un effet de lentille gravitationnelle, et qu'après on dresse une carte de l'univers en 3D, va-t-on la représenter telle qu'on la voit, avec une taille démesurée, ou va-t-on rectifier le tir en calculant sa taille réelle ? Dans ces exemples, pourtant issus de la RG, il n'existe qu'une réalité.

Quand on dit vu de loin, c'est une façon de parler, de situer entre eux les référentiels. Au lieu de dire "pour l'observateur éloigné du TN, vu de loin, le TN semble figé", je pourrais dire "une horloge située à l'horizon d'un TN ne bat plus si on l'a compare à une horloge restée sur terre". J'anticipe une objection sur le transport de l'information (une question du style: comment peut on comparer les horloges sans rayons lumineux?) simplement au nom de la RG qui prédit les TN et qui détermine le comportement des horloges dans ces situations.

[papy-alain]

Salut Mailou.

Pour une lentille gravitationnelle il n'y a pas de règle générale. L'image peut être déformée, agrandie (d'où le terme de lentille), dédoublée, etc. Tout dépend de la distance qui sépare les objets et si l'alignement avec l'observateur est parfait ou non. Mais dans tous les cas, l'image reçue ne reproduit pas fidèlement l'objet observé. Par exemple, dans le cas d'une double perception du même objet, si on accepte la même réalité conceptuelle de l'étoile gelée, alors on dira effectivement que la réalité est qu'il existe deux galaxies, là où il n'y en n'a qu'une pour l'observateur local.
Ta pièce jointe n'est pas encore validée, j'attends.

[papy-alain]

Quand on dit vu de loin, c'est une façon de parler, de situer entre eux les référentiels. Au lieu de dire "pour l'observateur éloigné du TN, vu de loin, le TN semble figé", je pourrais dire "une horloge située à l'horizon d'un TN ne bat plus si on l'a compare à une horloge restée sur terre". J'anticipe une objection sur le transport de l'information (une question du style: comment peut on comparer les horloges sans rayons lumineux?) simplement au nom de la RG qui prédit les TN et qui détermine le comportement des horloges dans ces situations.

Mouais, mais le cas du TN est très particulier, car on parle là d'une singularité gravitationnelle. Et le propre d'une singularité est justement de ne pouvoir être décrite par notre physique. L'horizon du TN et se qui se trouve derrière l'horizon échappe totalement à nos possibilités d'investigation, qu'elles soient observationnelles ou théoriques. Alors, pour ce qui est de l'étoile gelée, c'est un peu comme les religions : on y croit ou on n'y croit pas.

[Calvert]

Mouais, mais le cas du TN est très particulier, car on parle là d'une singularité gravitationnelle. Et le propre d'une singularité est justement de ne pouvoir être décrite par notre physique. L'horizon du TN et se qui se trouve derrière l'horizon échappe totalement à nos possibilités d'investigation, qu'elles soient observationnelles ou théoriques. Alors, pour ce qui est de l'étoile gelée, c'est un peu comme les religions : on y croit ou on n'y croit pas.

Petite précision, parce que je ne suis pas certain que ce soit bien clair pour toi : l'horizon n'est pas une singularité. La singularité est au centre. Les problèmes sur l'horizon n'apparaissent "que" dans certaines coordonnées (Schwartzschild, par exemple), mais disparaissent si on en choisit d'autre. C'est comme les cartes géographiques qui ne peuvent pas représenter les pôles avec les coordonnées standards (mais en changeant de coordonnées, on peut régler ce problème).

[invitebd9ed9fb]

Puisque c'est sécurisé, je suis le voyageur.
J'ai une énorme montre pour que l'observateur y fasse une lecture aisée.Plus je m'approche de l'horizon et plus il voit la petite aiguille ralentir.En fait la lumière lui parvenant sera tellement redshifté qu'il verra l'image s'assombrire au prorata de la distance me séparant de l'horizon, la longueur d'onde s'allongeant de façon exponentielle.Je suis bien incapable de faire le calcul, mon a-priori est que je serais invisible bien avant qu'il puisse voir la petite aiguille immobilée(temps-coordonnées nul).Si quelqu'un pouvait confirmer ou infirmer.Mais pour mon temps, pas de changement.Bref, le temps ne s'arrete pas.
Cordialement,

Bien sur qu'on ne voit plus rien, mais l'absence de lumière n’empêche pas le temps de ralentir. Donc inutile d'emporter une montre . Que dit la RG par le calcul ? Quel serait le ralentissement affectant un objet non visible car complétement redshifté et situé à proximité immédiate de l'horizon ?

[invite6c093f92]

Mouais, mais le cas du TN est très particulier, car on parle là d'une singularité gravitationnelle. Et le propre d'une singularité est justement de ne pouvoir être décrite par notre physique. L'horizon du TN et se qui se trouve derrière l'horizon échappe totalement à nos possibilités d'investigation, qu'elles soient observationnelles ou théoriques. Alors, pour ce qui est de l'étoile gelée, c'est un peu comme les religions : on y croit ou on n'y croit pas.

Tu a une mauvaise appréciation du truc, il n'y a pas de changement de la physique notable en deça de l'horizon, c'est au très proche voisinage de la singularité qui pose problème, donc la RG continue d'etre valide.
Cordialement,

[Zefram Cochrane]

Zefram, on arrête avec les théories perso, merci.

Bonjour,
Ok, mais puis je avoir la réponse à cette question : quel est le rayon d'un TN du point de vue d'un observateur local situé à une distance r (du point de vue de l'observateur de référence situé à l'oo) du cente du TN?

Cordialement
Zefram

[papy-alain]

Tu a une mauvaise appréciation du truc, il n'y a pas de changement de la physique notable en deça de l'horizon, c'est au très proche voisinage de la singularité qui pose problème, donc la RG continue d'etre valide.
Cordialement,

Ah, parce que dire que le temps est à l'arrêt sur l'horizon, ce n'est pas l'évocation d'une singularité ?

[Zefram Cochrane]

Petite précision, parce que je ne suis pas certain que ce soit bien clair pour toi : l'horizon n'est pas une singularité. La singularité est au centre. Les problèmes sur l'horizon n'apparaissent "que" dans certaines coordonnées (Schwartzschild, par exemple), mais disparaissent si on en choisit d'autre. C'est comme les cartes géographiques qui ne peuvent pas représenter les pôles avec les coordonnées standards (mais en changeant de coordonnées, on peut régler ce problème).

Pourrais tu nous expliquer le principe des coordoonées KS STP ?

[Calvert]

Pourrais tu nous expliquer le principe des coordoonées KS STP ?

Non, mes cours de relativité générale sont trop lointains et mes souvenirs à ce sujet pas très frais. Il faut attendre que quelqu'un de plus au fait que moi à ce sujet se manifeste (Deedee, Amanuensis, ...)

[invite6c093f92]

Que dit la RG par le calcul ? Quel serait le ralentissement affectant un objet non visible car complétement redshifté et situé à proximité immédiate de l'horizon ?

La RG dit que l'objet verra son temps-propre s'écouler plus lentement vu le champ de gravitation, et l'observateur "verra" le temps de l'objet retarder.Je ne vois toujours pas d'arret là-dedans, sauf à penser qu'il y a une orbite au dessus de l'horizon ou tau est nul....???
Cordialement,

[Mailou75]

Mais dans tous les cas, l'image reçue ne reproduit pas fidèlement l'objet observé.

Toute image nous arrive d'une géodésique "plus ou moins courbe", aucune n'est "fidèle" à 100%

Ta pièce jointe n'est pas encore validée, j'attends.

Rien à voir avec ça, c'est plus par rapport à la "courbure fossile",
j'essaye d'illustrer que la courbure n'a rien à voir avec la densité (l'état de l'objet),
mais qu'elle est juste liée à la masse.