Je tombe dans un trou noir, vois-je mes pieds ?

[Gilgamesh]

Y-a-t-il un moment, avant d’atteindre la singularité, ou on ne voit plus ses pieds dans la chute, ou, voit-on ses pieds tout le long du voyage.

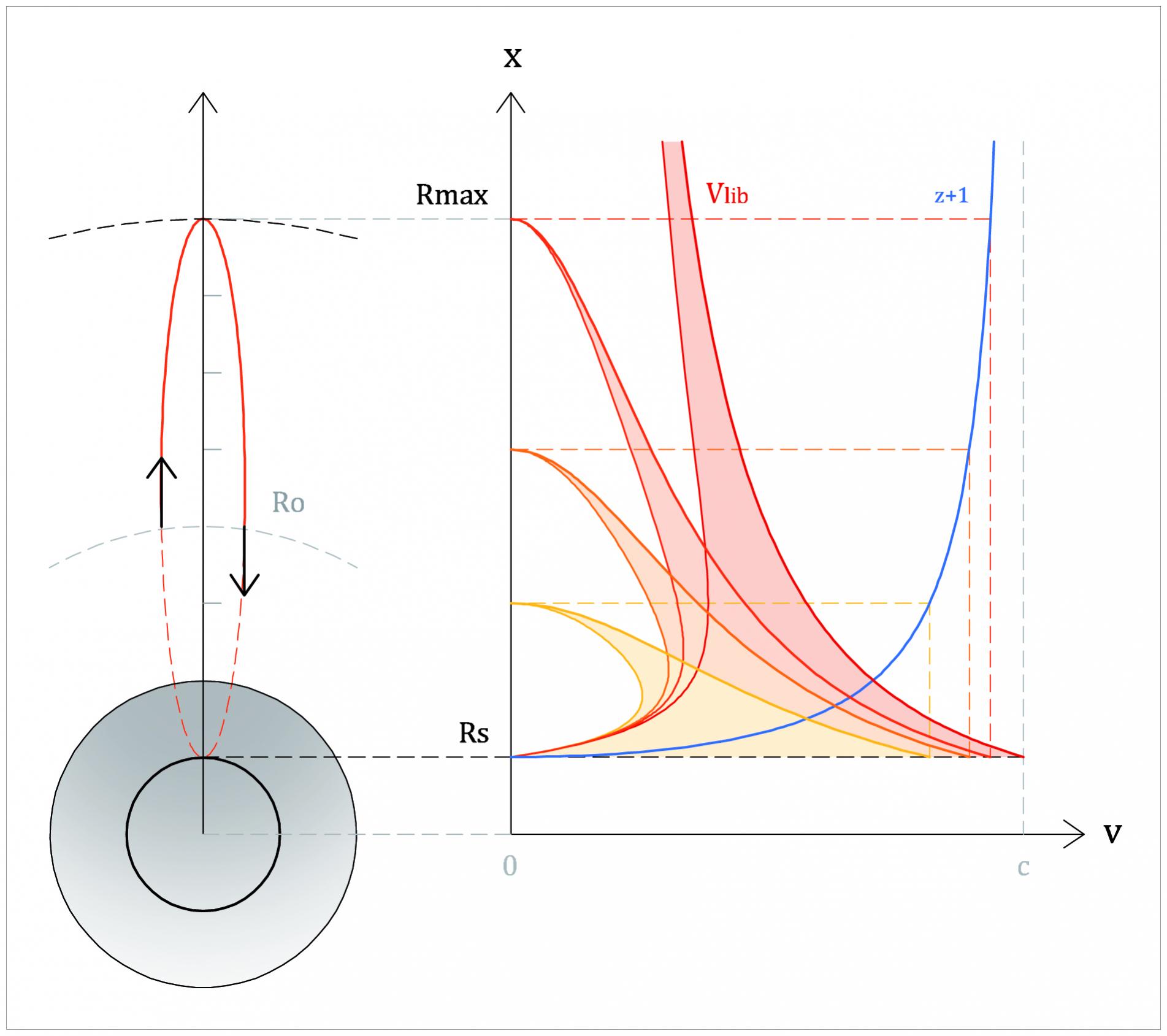
Le redshift est lié à la différence de potentiel entre deux points d'altitudes différentes. On imagine que le corps garde son intégrité et que cette différence d'altitude est constante. Par contre, la différence de potentiel au sein d'un corps n'est rien d'autre que l'effet de marée, qui est 1/R², avec R la distance au centre. C'est divergent, au sens que sa valeur va tendre vers +oo. Donc à un moment donné, oui, les pieds seront tellement redshiftés qu'on ne les verra plus.
-----

[invitee6f0086a]

Merci Gilgamesh,

Tout ceci fut fort intéressant, y a plus qu'à faire la manipe pour valider.

[Zefram Cochrane]

Non.
Il voit ses pieds tels qu'ils était un instant t=h/c avant, h est la distance de son oeil à ses pieds.

Bonsoir,
Comment démontre t'on ce résultat?
Cordialement,
Zefram

[invitee6f0086a]

Une dernière petite question :

Peut-on affirmer qu’une mesure (mon astronaute est tombé avec un petit labo d’expérimentation), faite à l’intérieur du trou noir, de c donnerait la valeur que l’on connait ?

Autrement dit, l’intérieur d’un trou noir, dépendant d’une physique non adaptée à la RG, serait-il envisageable que c, est une autre valeur ?

Merci,

[Gilgamesh]

Bonsoir,
Comment démontre t'on ce résultat?
Cordialement,
Zefram

On le pose !

Principe d'équivalence : en tout point de l'espace il existe un référentiel localement inertiel, le référentiel en chute libre dans le champ de gravitation qui est tel qu'aucune expérience (non-gravitationnelle) ne permet de le distinguer d'un référentiel non soumis à la gravitation.

Mesurer la vitesse de la lumière entre sa tête et ses pieds est incontestablement une expérience de physique non gravitationnelle.

Et la conséquence , après moult développement de ce principe c'est la Relativité Générale et les trou noir, en fait. Et donc c'est vrai y compris dans les trous noirs, forcément. C'est juste limité par l'effet de marée qui est la raison pour laquelle on dit que ce n'est que localement que ce principe est valable (dans un volume infinitésimale, au sens strict).

C'est pour ça que je suis impardonnable avec ma première réponse, vraiment.

daniel, cela répond également à ta question.

A ceci près que dans le cas d'un trou noir on envisage un champ tellement extrême, que la RG n'est plus valable pour traiter du centre, c'est pour ça qu'on le nomme "singularité". Mais on ne considère raisonnablement de modification substantielle qu'à un niveau sub-atomique (à l'échelle de Planck logiquement). Pour toute la partie sous horizon sauf un volume plus petit qu'un proton au centre, c'est valable.

[Zefram Cochrane]

Bonjour,

Je te remercie de ta réponse, Gilgamesh

On le pose !

Principe d'équivalence : en tout point de l'espace il existe un référentiel localement inertiel, le référentiel en chute libre dans le champ de gravitation qui est tel qu'aucune expérience (non-gravitationnelle) ne permet de le distinguer d'un référentiel non soumis à la gravitation.

Dans ce fil, on essaye de répondre à ce genre de question pour le cas stationnaire qui serait formulée ainsi dans le cas présent : si je mesure 2m à l'oo, conbien mesurerais-je à la surface d'une planète de rayon R ( point de vue de l'observateur à l'oo) et de masse M ?

http://forums.futura-sciences.com/as...ml#post4617415

http://forums.futura-sciences.com/as...ml#post4618316

Mesurer la vitesse de la lumière entre sa tête et ses pieds est incontestablement une expérience de physique non gravitationnelle.

Et la conséquence , après moult développement de ce principe c'est la Relativité Générale et les trou noir, en fait. Et donc c'est vrai y compris dans les trous noirs, forcément. C'est juste limité par l'effet de marée qui est la raison pour laquelle on dit que ce n'est que localement que ce principe est valable (dans un volume infinitésimale, au sens strict).

Je n'ai pas la même analyse que toi là dessus, à cause de l'effet marée qui traduit une différence d'accélération entre la tête et les pieds. La chute libre se ferait avec un taux d'accélération constant, effectivement, on pourrait dire que que c = h/t, mais il n'y aurait pas d'effet marée non plus.

Si je prend un tube creux rigide, que je rempli de sable, la partie basse du tube se termine par un miroir non solidaire du tube.

Je lâche verticalement le tube dans le sens de la longueur. Le tube démarre une chute libre vers le TN.

Dans la paroi du tube, il va se créer une tension parce que la paroi voudra résister à l'éttirement du à la différence d'accélération entre le sommet et la base du tube. Par contre le miroir va s'écarter de la base du tube et tomber de plus en plus vite vers le TN. La longueur de la colonne de sable va s'étirer au cours "du temps" entre le sommet et le miroir.

Si au sommet (ou au milieu si cela est plus pertinent à cause de l'effet marée) du tube se trouve un dispositif de lasers émettant des impulsions courtes. L'effet Shapiro, lié à la contraction des longueurs dans un champ de gravitation, Va faire que la vitesse apparente de la lumière sera de plus en plus faible.

C'est à dire que le rapport entre le temps effectif aller et retour et le temps déterminé par la distance séparant le sommet du tube où se trouve la source de l'emmeteur -récepteur des faisceaux lasers divisé par C, augmente au cours "du temps". La distance risque d'être assez chaude à déterminer vu que la source des faisceaux laser et le miroirs ne sont pas accélérés identiquement au cours de la même période.

Une fois passé l'horizon du TN, dont la taille reste à déterminer, puisque si ce rayon est égal à Rs pour l'observateur à l'oo qu'en est t'il pour un observateur stationnaire local et qu'en est t'il pour un observateur situé au sommet du tube?

Une fois passé l'horizon je ne sais pas, d'autant que dans la vidéo d'Alain Riazuelo,
http://forums.futura-sciences.com/as...rences-tn.html

La chute libre concernait un observateur infinitésiment petit, et que lorsque cet observateur franchit l'horizon du TN, celui-ci est vu avec un angle de 84°. Comme dirait alain_r exercice.. donc.


Cordialement,
Zefram

[Zefram Cochrane]

Je pense qu'il est plus pertinent de mettre le dispositif des lasers au milieu du tube et de placer un miroir à la base et au sommet du tube.
l'effet marée s'appliquant de façon symétrique, la rigidité du tube va empêcher le tube de s'étirer de part et d'autre du centre du tube sous l'effet de la différence d'accélération.

Si on met une balance à chaque extrémité du tube et solidaire de celui-ci un observateur qui aurait les pieds sur la balance et la tête orienté vers le milieu du tube, aurait un poids il verrait le miroir placé initialement à son niveau s'écarter de l'extrémité concernée du tube et le sable s'écouler, accélérer comme s'il tombait dans un champ de gravitation.

Cordialement,
Zefram

[inviteccac9361]

A ceci près que dans le cas d'un trou noir on envisage un champ tellement extrême, que la RG n'est plus valable pour traiter du centre, c'est pour ça qu'on le nomme "singularité".

Tout à fait, la singularité de la RG se situ "au niveau" de r=0

Mais on ne considère raisonnablement de modification substantielle qu'à un niveau sub-atomique (à l'échelle de Planck logiquement). Pour toute la partie sous horizon sauf un volume plus petit qu'un proton au centre, c'est valable.

Par contre, ici, c'est à mon avis un peu plus compliqué.
On ne peut dire qu'on sait modéliser l'interieur du trou noir avec la RG au delà de r=0+rayon du proton que si l'espace-temps est "lisse".

Or ce n'est très certainement pas le cas.
On imagine assez bien que la matière (on peut même dire l'espace-temps) ne se laisse pas compresser uniformément jusqu'à r+petit sigma.
Il y a d'un coté les lois théoriques, la RG par exemple, qui fournit un cadre, et de l'autre les phénomènes (en vertu des lois théoriques).
La matière et l'énergie sont des phénomènes, et la théorie ne dit rien des phénomènes, elle les autorise ou les interdit simplement.

Ce qui a amené à un moment à supposer que la RG devait être étendue (au dela de l'horizon donc) et incorporée dans une théorie à 5 dimensions.
Cette théorie avait l'avantage de fournir une vision relativement compréhensible de l'interieur d'un trou noir sous la forme de "couches" pour chaque état de la matière, dont les nivaux étaient quantifiées. (bien au delà de r=0 donc).
(Ce qui est amusant ici, il me semble, c'est qu'on retrouve le principe de l'horizon qui n'existe que pour l'observateur à l'infini (dans sa couche) pour chaque couche, comme lorsqu'on voit le trou noir depuis la Terre (serions-nous dans une "couche" ?)).

Cette approche a été abandonnée car mathématiquement elle ne tenait pas lorsqu'on avait affaire à certains types de particules (les fermions).
Elle a été remplacée par la théorie des cordes pour cette raison, suite à l'échec mathématique. (je simplifie...)

D’autres tentatives de quantification ont été faites (par exemple les formulations " covariantes de Lorentz ", étudiées en particulier par Bryce S. DeWitt), mais elles se sont toutes heurtées à de graves difficultés.
En somme, la quantification directe de la théorie d’Einstein pose problème.

Peut-être faut-il alors considérer que la relativité générale n’est pas une théorie fondamentale, mais seulement une théorie effective qui découle, comme approximation macroscopique, d’une théorie unifiée sous-jacente.

Cette ambitieuse vision unificatrice est devenue dominante depuis le début des années soixante-dix, après le succès de l’unification des forces non gravitationnelles, sous l’influence conjuguée de nouvelles idées (supersymétrie, cordes) et de l’idée plus ancienne (due à Theodor Kaluza et Oskar Klein) que l’espace-temps a peut-être plus de quatre dimensions.

Historiquement, les premières tentatives d’unification ne comprenaient que la relativité générale et l’électromagnétisme, décrit par le quadripotentiel Aµ.
Kaluza et Klein réalisèrent que les champs gμν et Aµ, qui apparaissent séparés dans l’espace-temps à quatre dimensions (D = 4), pouvaient être unifiés dans la métrique riemannienne d’un espace-temps à cinq dimensions (D = 5) : gMN = (gμν , gµ5, g55) ; ce procédé fait apparaître un champ scalaire supplémentaire en D = 4.

Afin d’expliquer pourquoi on ne voit pas la cinquième dimension, on peut alors supposer qu’elle se referme sur elle-même en cercles de rayon ≈ l0.
Une telle périodicité par rapport à la cinquième dimension permettrait aussi d’expliquer la quantification de la charge électrique.
(Ces idées peuvent se généraliser à l’unification de la relativité générale avec les théories de jauge non abéliennes de Yang-Mills.)

De telles tentatives d’unification " géométrique " furent abandonnées (sauf par Einstein lui-même) quand furent découvertes de plus en plus de particules " élémentaires ", comprenant notamment des particules de spin 1/2 (électron, neutrino, quark...) qui sont décrites par des champs fermioniques de nature essentiellement quantique, sans analogues classiques.

http://www-cosmosaf.iap.fr/RELATIVIT...20Thibault.htm

Ceci veut dire probablement que l'interieur du trou noir au delà de l'horizon subit déja des "transformations" bien au delà de r=0+sigma mais dont nous n'avons finalement pas idée.

[Gilgamesh]

On ne peut dire qu'on sait modéliser l'interieur du trou noir avec la RG au delà de r=0+rayon du proton que si l'espace-temps est "lisse".
Or ce n'est très certainement pas le cas.

Il est lisse en faible champ de gravité au moins dans les limites mesurées de l'ordre de 10^-19 m. Une forte courbure peut changer les chose, mais y'a de la marge.

On imagine assez bien que la matière (on peut même dire l'espace-temps) ne se laisse pas compresser uniformément jusqu'à r+petit sigma.
Il y a d'un coté les lois théoriques, la RG par exemple, qui fournit un cadre, et de l'autre les phénomènes (en vertu des lois théoriques).
La matière et l'énergie sont des phénomènes, et la théorie ne dit rien des phénomènes, elle les autorise ou les interdit simplement.
Ce qui a amené à un moment à supposer que la RG devait être étendue (au dela de l'horizon donc) et incorporée dans une théorie à 5 dimensions.
Cette théorie avait l'avantage de fournir une vision relativement compréhensible de l'interieur d'un trou noir sous la forme de "couches" pour chaque état de la matière, dont les nivaux étaient quantifiées. (bien au delà de r=0 donc).
(Ce qui est amusant ici, il me semble, c'est qu'on retrouve le principe de l'horizon qui n'existe que pour l'observateur à l'infini (dans sa couche) pour chaque couche, comme lorsqu'on voit le trou noir depuis la Terre (serions-nous dans une "couche" ?)).

Cette approche a été abandonnée car mathématiquement elle ne tenait pas lorsqu'on avait affaire à certains types de particules (les fermions).
Elle a été remplacée par la théorie des cordes pour cette raison, suite à l'échec mathématique. (je simplifie...)

http://www-cosmosaf.iap.fr/RELATIVIT...20Thibault.htm

Ceci veut dire probablement que l'interieur du trou noir au delà de l'horizon subit déja des "transformations" bien au delà de r=0+sigma mais dont nous n'avons finalement pas idée.

L'approche de Kaluza Klein est intéressante et pionnière à n'en pas douter, mais l'idée de compression d'un référentiel d'espace temps ne me semble pas pertinente (de courbure, oui). Par ailleurs je ne connais pas de développement de la théorie KK qui aborde les trous noirs de cette façon. Déjà évidemment, la théorie date de 1921, bien avant que les trou noirs soient proprement conceptualisés, mais même avec son "revevival" au sein de la théorie des cordes, je ne vois pas apparaître la notion de couches sous forme d'horizons successifs. Tu tiens ça d'où ?

[Gilgamesh]

Je n'ai pas la même analyse que toi là dessus, à cause de l'effet marée qui traduit une différence d'accélération entre la tête et les pieds. La chute libre se ferait avec un taux d'accélération constant, effectivement, on pourrait dire que que c = h/t, mais il n'y aurait pas d'effet marée non plus.

Je ne comprend pas la partie en gras de la phrase ni le sens général de ton propos.

Je dis que c'est une chute libre normal, à l'effet de marée près. Et tu me dis que tu n'est pas d'accord parce ce qu'il y un effet de marée. Evidemment qu'il y a de nombreux effets du au gradient de gravité formidable aux abord d'un trou noir, et d'autant plus qu'il est de faible masse et qu'on est proche de l'horizon. Durant toute la discusion, il en a été fait abstraction juste par commodité, pas pour dire que ça n'a pas d'effet.

[Zefram Cochrane]

Je ne voulais pas être désagréable mais entre le fait d'être absolument d'accord ou absolument pas d'accord il y a toute une nuance rendu difficile à exprimer sur le fait que l'on peut être d'accord sur certains points et être en désaccord sur d'autres : quand tu évoques le principe d'équivalence, je suis d'accord, si tu dis qu'on peut négliger l'effet marée, je ne le suis plus.

La question étant : Est ce que je [B] vois [/TEX] mes pieds si je mesure deux mètres et que je suis en chute libre à l'intérieur du TN. Je dis que pour répondre par oui ou par non à cette question et intuitivement, je dirai même que cela doit dépendre de l'altitude de départ, et que peut être je pourrais être en mesure de voir mes pieds tout en étant en dessous de l'horizon du TN mais jusqu'à une certaine distance de la singularité centrale.

Cette question peut être identique à celle ci :

soit deux observateurs situé aux extrémités d'un tube fermé de longueur L (comment la déterminer ?) ) en chute libre à une distance R (du point de vue de l'observateur à l'oo, qu'est ce que cela donne du point de vue des observateurs ? ) d'un TN de masse M. Est ce que les observateurs se voient quelle que soit R?

Le point intéressant que m'a fait découvrir cette discussion est que chaque observateur est collé à son extrémité du tube du fait de l'accélération différentielle engendrée par l'effet marée. Accélération qui est, selon le principe d'équivalence,localement équivalente à un champ de gravitation.

Cordialement,
Zefram

[Amanuensis]

C'est quoi la "distance à la singularité" pour un événement à l'intérieur?

[Deedee81]

Salut,

C'est quoi la "distance à la singularité" pour un événement à l'intérieur?

Je suppose que Zefram veut dire soit la coordonnée de Schwartzchild r, soit le temps propre (pour le coup, ça ne pose pas trop de problème).

Zefram,

Par contre, attention avec une distance étalon ou un tube de longueur L. Ca peut n'avoir aucun sens sous l'horizon car l'étirement peut être "irrésistible" et cette notion de distance au sens habituel peut perdre tout son sens.

[Amanuensis]

Je suppose que Zefram veut dire soit la coordonnée de Schwartzchild r

C'est une durée, pas une distance

Sinon, l'idée c'est que Zefram apprenne, pas qu'on réponde à sa place.

Par contre, attention avec une distance étalon ou un tube de longueur L. Ca peut n'avoir aucun sens sous l'horizon car l'étirement peut être "irrésistible" et cette notion de distance au sens habituel peut perdre tout son sens.

Il s'agit de longueur. Je ne vois pas trop de quelle "irrésistibilité" il s'agit (à part en pratique, mais qui s'en occupe?), par contre la simultanéité utilisée serait intéressante à préciser...

[inviteccac9361]

L'approche de Kaluza Klein est intéressante et pionnière à n'en pas douter, mais l'idée de compression d'un référentiel d'espace temps ne me semble pas pertinente (de courbure, oui). Par ailleurs je ne connais pas de développement de la théorie KK qui aborde les trous noirs de cette façon. Déjà évidemment, la théorie date de 1921, bien avant que les trou noirs soient proprement conceptualisés, mais même avec son "revevival" au sein de la théorie des cordes, je ne vois pas apparaître la notion de couches sous forme d'horizons successifs. Tu tiens ça d'où ?

De courbure effectivement, c'est plus pertinent de le dire de cette manière vis à vis de la théorie.
J'admet aussi que l'affaire des transitions de phase (que j'associe à des "couches") sont ici une interpretation personnelle basée sur une autre mathématisation de la notion de courbure (trop personnel pour ce coup là, et je m'en excuse)

Voir sinon cet article pour ce qui concerne les transitions de phase (les "phénomènes").

L’effet Casimir a l’intérêt de nous introduire dans un domaine de la physique en pleine émergence, c’est le cas de le dire.
C’est celui consistant à mettre en évidence des effets quantiques se manifestant à l’échelle macroscopique.
Nous avons précédemment présenté l’ouvrage que, à tort ou à raison, nous pensons fondateur, celui du physicien Robert Laughlin(6).

L’auteur base tout son plaidoyer pour une physique différente sur les cas qu’il connaît bien, puisqu’ils lui ont permis d’obtenir son prix Nobel, ceux des matériaux super-conducteurs et super-fluides.
Ces matériaux, à certaines conditions de température, enregistrent des transitions de phase qui ne sont pas descriptibles par la physique macroscopique.

C’est plus précisément au moment où le matériau bascule, par exemple, d’un état magnétique à un état non magnétique, que se produit l’état non descriptible, c’est-à-dire l’émergence du principe d’incertitude de la MQ.
Il n’est plus possible à ce moment de décrire l’évènement en termes déterministes.
Autrement dit, à des conditions de température et de pression données, on verrait ainsi s’ouvrir en ce court instant (non mesurable) une fenêtre sur le vide quantique.
On parle d’un état de criticité quantique (quantum criticality).

http://www.automatesintelligents.com...gravastar.html

[Amanuensis]

Déjà évidemment, la théorie date de 1921, bien avant que les trou noirs soient proprement conceptualisés

Schwarzschild est décédé en 1916, non?

[Gilgamesh]

Schwarzschild est décédé en 1916, non?

C'est vrai, mais que le concept n'est devenu mâture que dans les années 60.

[Zefram Cochrane]

Salut,



Je suppose que Zefram veut dire soit la coordonnée de Schwartzchild r, soit le temps propre (pour le coup, ça ne pose pas trop de problème).

Zefram,

Par contre, attention avec une distance étalon ou un tube de longueur L. Ca peut n'avoir aucun sens sous l'horizon car l'étirement peut être "irrésistible" et cette notion de distance au sens habituel peut perdre tout son sens.

Bonsoir, je pensais à la coordonnée r.

Voici grosso modo comment il me semble que le problème se présente soit O O' O'' trois observateurs respectivement situées au sommet du tube, au milieu et à la base du tube. O et O'' ont la tête orientée vers O'. onva dire que le tube est en chute libre depuis un endroit très éloigné du TN (r = oo ). à r = oo la longueur du tube est 2L

Les éléments que j'ai est que le tube va chuter à la vitesse de libération en direction du TN .

l'observateur O' est en chute libre.
A l'endroit où se trouve O'' la vitesse de libération est supérieur à celle du tube, la rigidité supposée infinie du tube va maintenir la vitesse de O'' à la vitesse de O' et donc O'' va ressentir une accélérétion propre.
A l'inverse la vitesse de libération de l'endroit où se trouve O est inférieure à celle de O'. Le tube va entraîner O dans sa chute. Pareil, O va ressentir une accélération propre.

La question est quelle sont les coordonnée de O O' et O'', et à quelle distance il se verront les uns les autres.

Tout un programme.

Cordialement,
Zefram

[invitee6f0086a]

Donc, on voit bien ses pieds, et les photons vont à c vers la tête. Ces mêmes photons vont d’ailleurs dépasser la tête (enfin, je crois).

L’astronaute doit aller très très vite, alors par rapport à quoi, et dans quelle unité de longueur !??.

De plus, l’écoulement de son Temps propre par rapport à un observateur à l’extérieur, doit être méga lent.

J’ai bon ?

[invite34567123333]

De plus, l’écoulement de son Temps propre par rapport à un observateur à l’extérieur, doit être méga lent.

Le temps propre est le même pour tout le monde : 1s/s ; il ne ralentit pas.

Pour un observateur extérieur, notre casse-cou termine son aventure à jamais figé sur l'horizon et sa montre est arrêtée.

[invitee6f0086a]

Le temps propre est le même pour tout le monde : 1s/s ; il ne ralentit pas.

Pour un observateur extérieur, notre casse-cou termine son aventure à jamais figé sur l'horizon et sa montre est arrêtée.

Non, pour nous, il tombera « au fond », sinon les trous noirs n’aurait jamais rien « ingurgités », hors ce n’est pas le cas.

Je n’ai toujours pas compris ce paradoxe, concept de simultanéité je crois.

[invite6c093f92]

Bonsoir,
Non, pour nous, observateur, son image restera "figé" sur l'horizon, et ne nous sera visible que un certains temps, pour le malheureux bien sur, il passe l'horizon et "tombera au fond".
Cordialement,

[invite34567123333]

pour le malheureux bien sur, il passe l'horizon et "tombera au fond".
Cordialement,

De son propre point de vue bien sûr, et en un temps fini.

Oublions "l'image", et dites moi alors au bout de combien de temps (mesuré à l'extérieur) l'observateur tombe au fond...

Pour moi cette question n'a aucune signification car ces évènements ne sont plus causalement reliés et la "mesure" extérieure à l'instant t (de ce qui se passe à l'intérieur) est impossible. (vrai ou faux ?)

[invite6c093f92]

Oublions "l'image", et dites moi alors au bout de combien de temps (mesuré à l'extérieur) l'observateur tombe au fond...[/U]

Je ne comprends pas....on dis la meme chose non?
Pour nous , l' observation que nous pouvons faire du sujet, sera une image qui semble se figer sur l'horizon, cette "image", " s'assombrissant" au pro-rata de l'allongement de la longueur d'onde de la lumière nous parvenant.
Cordialement,

[invitee6f0086a]

Je ne comprends pas....on dis la meme chose non?
Pour nous , l' observation que nous pouvons faire du sujet, sera une image qui semble se figer sur l'horizon, cette "image", " s'assombrissant" au pro-rata de l'allongement de la longueur d'onde de la lumière nous parvenant.
Cordialement,

J’étais au courant de cette image fossile, mais si je vois, de l’extérieur cette image, cela voudrait-il dire que des photons sortent du trou noir, hors rien ne sort d'un TN.

Moi qui croyais maitriser les trous noirs , me voila de nouveau perdu.

[invite34567123333]

Je ne comprends pas....on dis la meme chose non?

Je pense que nous sommes d'accord effectivement.

[invite34567123333]

J’étais au courant de cette image fossile, mais si je vois, de l’extérieur cette image, cela voudrait-il dire que des photons sortent du trou noir, hors rien ne sort d'un TN.

Non, ils ne "sortent pas" du trou noir.
Ceux que vous voyez sont émis depuis un peu au dessus de l'horizon, mais de moins en moins et avec de moins en moins d'énergie au fur et à mesure que c'est émis proche de l'horizon.
(je ne parle pas de rayonnement Hawking ici, on est resté dans le cadre "classique").

Mais je crois qu'on dévie de la question initiale..

[invitee6f0086a]

Bien compris, merci !

[Zefram Cochrane]

Bonsoir Didier (dont la messagerie est pleine)

Je ne comprends pas....on dis la meme chose non?
Pour nous , l' observation que nous pouvons faire du sujet, sera une image qui semble se figer sur l'horizon, cette "image", " s'assombrissant" au pro-rata de l'allongement de la longueur d'onde de la lumière nous parvenant.
Cordialement,

En RG (dans le cadre de la métrique de Schwarzschild) la vitesse coordonnée diffère de la vitesse instantannée ( peut on parler de vitesse effective?) contrairement à la RR où elles sont égales.



Le graph de Mailou ci dessus présente différentes vitesse où le voyageur est parti à une vitesse nulle depuis des altitudes différentes (toutes supérieures à Rs) la branche de droite atteint l'horizon du TN à une vitesse < c , c'est la vitesse effective du voyageur. La branche de gauche est la vitesse coordonnée, ici 'mesurée' par l'observateur à l'oo ( elle serait mesurée par l'observateur stationnaire situé à l'altitude de départ du voyageur, je pense sans certitude qu'elle serait différente).

Comme on peut le constater sur le graph. La vitesse coordonnée augmente, atteint un maximum puis diminue jusquà devenir nulle au niveau de l'horizon du TN; ceci est valable pour n'importe quel observateur stationnaire externe au TN.

La raison est la suivante est que la vitesse coordonnée de la lumière diminue dans un champ de gravitation pour devenir nulle également au niveau de l'horizon du TN. Hors l'énergie du voyageur se conserve lors d'une chute libre et cette énergie comprend une composante potentielle et une composante cinétique (comme en RR). Ce qui veut dire que fondamentalement ( et non pas dans la forme) le principe du TEC qui dit qu'en chute libre dans un champ de gravitation, l'énergie potentielle de gravitation se transforme en énergie cinétique reste valable.

Or, si la vitesse de la lumière coordonnée (contrairement à la vitesse de la lumière qui localement reste, consensuellement, constante) diminue dans un champ de gravitation, il arrivera un moment où la vitesse de chute coordonnée ne pourra plus augmenter sans transgresser le principe de la conservation de l'énergie du voyageur. Pour, remédier à ce problème, la vitesse de chute doit donc diminuer à partir d'une altitude qui dépend de l'altitude de départ.
Donc pour rebondir sur le sujet, comme sur toute sa longueur, mon corps est entraîné à la vitesse de chute du centre de masse, il est clair que la vitesse coordonnée de la lumière n'est pas la même au niveau de la tête et au niveau des pieds, pour une fourmi observatrice situé au niveau du centre de masse. Je ne suis pas certain que la vitesse de lumière soit constante sur la longueur de mon corps et donc que je serai en mesure de voir mes pieds en deça d'une certaine altitude ( probablement inférieure à RS.

Cordialement,
Zefram

[Amanuensis]

Non, pour nous, il tombera « au fond », sinon les trous noirs n’aurait jamais rien « ingurgités », hors ce n’est pas le cas.

Mais c'est le cas.

Pour l'observateur à l'infini, le trou noir n'ingurgite rien, au sens où cet observateur ne voit pas, n'a jamais vu et ne verra jamais de la matière passer l'horizon. Soit c'est un "trou noir primordial", et l'observateur l'a toujours "vu" tel qu'il est, soit c'est un trou noir en formation (une masse en effondrement inéluctable), et l'observateur à l'infini ne voit que de la matière se figeant sur l'horizon.