Dans un trou noir, il est ou « géométriquement parlant» l’horizon des événements ?

[invitee6f0086a]

Bonjour à tous,

Merci d’attendre la validation de l’images, car cela devrait beaucoup aider à la compréhension de ma question qui est peut-être mal formulée.



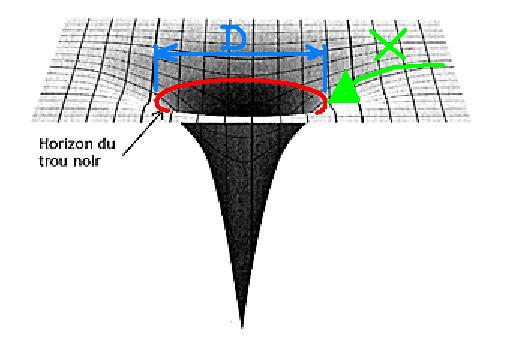
Dans cet exemple (l’image) d’un trou noir de 10 masses solaires (par exemple), quelle est la valeur de D, et surtout à partir de quelle « distance X » et par rapport à quoi détermine-t-on, pour un observateur à l’extérieur, la position de l’horizon des événements (distance à partir de laquelle les photons ne sortent plus).

Je suis également intéressé par les formules qui donnent ces valeurs.

PS : je sais bien que l’image donne une représentation très vulgarisé du puits gravitationnel d’un TN, mais c’est peut-être en accord avec la question.

Il faut bien que le pilote du vaisseau puisse calculer le moment ou il aura atteint le point de non retour, ça peut aider ! et donc à partir de quelles données fera-t-il ce calcul. Tiens ! le calcul de ce point de non retour est-il le même, fait par un observateur extérieur, et par le pilote du vaisseau ?

En espérant avoir été clair, merci pour vos réponses,
-----

[Amanuensis]

La valeur de D dépend de tas de conventions, pas de valeur unique. Il est bien plus facile de donner un sens à la longueur du cercle rouge.

Pour un trou noir de Schwarzschild, ce périmètre vaut 4π GM/c².

En relativité générale la notion de distance pose souvent des difficultés. On peut rester sur un terrain "sûr" si on demande la longueur d'un chemin de genre spatial.

La question sur la longueur D n'est pas posée comme celle d'un chemin.

Alors que le cercle rouge est bien un chemin. Qu'il fasse partie de l'horizon pose quelques difficultés, en particulier si on utilise la métrique de Schwarzschild. Mais même dans ce cas on peut s'en tirer en regardant la limite de la longueur de cercles un peu plus extérieurs. Et cette limite est finie, valant 4πGM/c².

Pour la distance X, c'est pareil, il faudrait préciser le chemin (en 4D) dont on demande la longueur. C'est peut-être vu comme bizarre, mais le dessin est insuffisant pour préciser ce chemin.

Différentes possibilités viennent à l'esprit, principalement:

- Le chemin λ -> (0, λ, 0, 0) avec λ dans ]r_s, r[ en coordonnées de Schwarzschild

- le chemin de chute libre radiale entre (0, r, 0, 0) et le passage de l'horizon, en précisant la vitesse initiale (par exemple en coordonnées de Schw.)

Quand l'équation d'un chemin est donnée dans un système de coordonnées, le calcul de la longueur est "simplement" l'intégrale de la "métrique" le long du chemin. En maths, si λ -> M(λ) est une équation du chemin pour λ allant de λ1 à λ2, sa longueur est

,

où g(., .) est la métrique (interprétée comme forme bilinéaire) en signature -+++.

Même si ce n'est pas toujours facile à calculer, cette formule donne une définition rigoureuse, qui peut être appliquée par n'importe qui, et qui donne un résultat indépendant du choix de système de coordonnées.

Mais on ne peut l'utiliser qu'à condition que le chemin soit décrit précisément, ce qui n'est pas le cas pour D ou X sur la figure.

La RG, et encore plus un cas comme un "trou noir", n'est pas intuitive, rares sont les questions qui peuvent se résoudre "visuellement" ou par interprétation. En s'imposant de travailler "de manière bourrin", avec des coordonnées, donc avec un système de coordonnées bien précisé et dans lequel la forme métrique est connue, on peut aboutir à des réponses en évitant les pièges que nous tend notre intuition. Et ensuite, connaissant le résultat "bourrin" on peut essayer de l'interpréter.

Par exemple, pour la longueur du cercle rouge, on peut prendre les chemins suivants λ -> (0, r, pi/2, λ), en coordonnées de Schwarzschild, pour λ parcourant 0 à 2π, et r>2GM/c² constant. On alors dM/dλ = (0,0,0,1), g(dM/dλ, d/dλ) = r² (c'est le terme en dphi² de la métrique), et donc l'intégrale de sa racine carrée entre 0 à 2π vaut 2π r. Quand r tend vers 2GM/c², cette longueur tend vers 4πGM/c².

[En fait, c'est par définition même de la métrique de Schwarschild ; comme indiqué dans https://en.wikipedia.org/wiki/Schwarzschild_metric, "r is the radial coordinate (measured as the circumference, divided by 2π, of a sphere centered around the massive body)".]

Autre exemple (tj. en coordonnées de Schw.), pour X défini comme la longueur de λ -> (0, λ, pi/2, 0) entre r et rs= 2GM/c², dM/dλ = (0, 1, 0, 0), g(dM/dλ, d/dλ) = 1/(λ/rs-1) (c'est le terme de dr² de la métrique). Un petit calcul donne

[invitee6f0086a]

Merci Amanuencis,

Je me doutais que se n’était pas simple comme calcul, mais pas à ce point la.

Donc, si je décide d’aller dans le future à bord de mon vaisseau, en orbitant tout proche de l’horizon, c’est un voyage très risqué car la marge d’erreur est très grande et surtout calculable à la louche. C’est ça ?

[Amanuensis]

Mon point n'était pas tant sur la difficulté ou non des calculs, mais sur la difficulté à exprimer rigoureusement une question de la forme "quelle est la distance X?" dans le contexte de la RG, et plus précisément quand les effets gravitationnels sont très importants.

[A voir en vidéo sur Futura]

[invitee6f0086a]

Mon point n'était pas tant sur la difficulté ou non des calculs, mais sur la difficulté à exprimer rigoureusement une question de la forme "quelle est la distance X?" dans le contexte de la RG, et plus précisément quand les effets gravitationnels sont très importants.

Bonsoir,

Quand j’ai posé la question, je savais bien que la représentation de la figure poserait problème, mais je n’avais que ça sous la main.

Aussi bien, la formulation de la question concernant X pourrait aider à se faire une idée.

D’après toi Amanuensis, comment aurait-il fallut poser la question, et avec quelle style de schéma ?

Je sais bien que ce n’est pas à toi de poser la question, mais dans ce cas précis du trou noir, ou il y a beaucoup de paramètres, pas facile à compiler pour l’esprit humain car non intuitif, la formulation de la question est capital, et devrait permettre de comprendre la complexité pour résoudre ce X.

Aussi bien, formuler X n’a pas de sens, je trouverais cela tout de même étonnant.

Tous les avis sont bien sûr constructifs!

[Amanuensis]

Quand j’ai posé la question, je savais bien que la représentation de la figure poserait problème, mais je n’avais que ça sous la main.

Ce n'est pas la figure le problème. (Elle pose bien des problèmes, mais ce n'est pas le sujet.)

D’après toi Amanuensis, comment aurait-il fallut poser la question (...) ?

C'est dans ma réponse, j'avais pris soin de donner des exemples, etc.

[jo314]

Pour un trou noir de Schwarzschild, ce périmètre vaut 4π GM/c².

Le rayon de Schwarzschild vaut r = 2GM/c²
Vous dites que le périmètre de l'horizon est p = 4π GM/c²
Je pensais qu'au voisinage d'un trou noir, la courbure de l'espace temps était très forte et qu'en conséquence on était plus dans un espace euclidien donc p ≠ 2π r

La valeur de D dépend de tas de conventions, pas de valeur unique. Il est bien plus facile de donner un sens à la longueur du cercle rouge.
[...]
En relativité générale la notion de distance pose souvent des difficultés. On peut rester sur un terrain "sûr" si on demande la longueur d'un chemin de genre spatial.
La question sur la longueur D n'est pas posée comme celle d'un chemin.

Si je comprend bien le rayon de Schwarzschild ne serait égal à r = D/2 = 2GM/c² que si on prend certaines conventions (lesquelles ?), pourriez-vous nous donner plus de précisions ?
En d'autres termes, si je tombe dans un trou noir, entre le moment où je franchis l'horizon et le moment où je m'écrase sur la singularité, quelle distance est-ce que j'aurais parcouru :
- par rapport à un observateur situé à l'infini ?
- par rapport à l'horizon ?
- par rapport à la singularité ?
Comme on est dans un espace en effondrement, donc je conçois que la réponse n'est pas forcément simple.

[Amanuensis]

Le rayon de Schwarzschild vaut r = 2GM/c²
Vous dites que le périmètre de l'horizon est p = 4π GM/c²
Je pensais qu'au voisinage d'un trou noir, la courbure de l'espace temps était très forte et qu'en conséquence on était plus dans un espace euclidien donc p ≠ 2π r

Il y a des cas où c'est différent, mais cela n'interdit pas des cas particuliers avec égalité.

Si je comprend bien le rayon de Schwarzschild ne serait égal à r = D/2 = 2GM/c² que si on prend certaines conventions (lesquelles ?), pourriez-vous nous donner plus de précisions ?

La seule convention est juste de définir le rayon de Schw. comme 1/2pi le périmètre! (Et plus généralement d'utiliser comme système de coordonnée un "r" défini comme 1/2pi le périmètre d'un cercle lui-même défini à partir de l'hypothèse de symétrie sphérique.)

En d'autres termes, si je tombe dans un trou noir, entre le moment où je franchis l'horizon et le moment où je m'écrase sur la singularité, quelle distance est-ce que j'aurais parcouru :
- par rapport à un observateur situé à l'infini ?
- par rapport à l'horizon ?

Il y a plein d'endroits où la formule est donnée, y compris divers fils sur le forum. Peut-être quelqu'un d'autre aura-t-il les moyens de donner une référence rapidement. Mais ce n'est pas la différence de coordonnée "r".

- par rapport à la singularité ?

Plus compliqué de donner un sens à cela (la singularité n'est pas un "lieu").

[jo314]

Merci pour ces réponses.

Plus compliqué de donner un sens à cela (la singularité n'est pas un "lieu").

Je sais que la singularité est plutôt de type temporelle , c.a.d qu'elle est toujours située dans le futur d'un observateur (quel qu'il soit), mais au moment ou je m'écrase dessus je dois bien avoir parcourus une certaine distance dans un référentiel donné, non ?

[Amanuensis]

Oui, mais l'espace-temps en question étant statique pour r>r_s, on peut parler de la distance à des lieux "statiques" comme l'infini ou l'horizon. Pour la singularité faut parler d'une trajectoire particulière, et il n'y en pas qu'une.

[invitee6f0086a]

Je croyais que la RG n’est pas adapter pour décrire l’intérieur d’un trou noir, et cela, plus on s’approche de la singularité.

Je dirais même plus, le principe même de dire qu’il y a une singularité est un non sens, car la RG n’est pas adapté. De même, débattre sur une notion de distance vers elle n’a aucun intérêt puisque nous n’avons aucune théorie adapté à cet environnement.

Je vais même être volontairement provoquant , discuter de ce qu’il y a derrière l’horizon n’a aucun intérêt actuellement, on peut dire tout et n’importe quoi.

A moins que quelque chose m’échappe …

[invitee6f0086a]

J’ai même presque envi de dire que jusqu’à l’horizon, nous sommes dans notre univers, et qu’après, nous sommes « ailleurs » car non régit par la RG, qui décrit « notre » univers comme nous le concevons (en tout cas à 5%).

Le « ailleurs » est aussi argumenté par le fait nous n’avons aucune information qui ressort d’un TN.
Quant à l’information de l’existence d’une grande masse, ce n’est pas vraiment une information, juste qu’il y a quelque chose, le « ailleurs ».

Je vois l’horizon comme la surface d’une sphère extrêmement petite (dans notre métrique) pour accumuler tant de matière. Cela est totalement inconcevable d’après nos lois, et donc notre conception de l’univers.

[Amanuensis]

J’ai même presque envi de dire que jusqu’à l’horizon, nous sommes dans notre univers, et qu’après, nous sommes « ailleurs » car non régit par la RG

N'importe quoi.

Le reste pas mieux.

[invitee6f0086a]

…Plus compliqué de donner un sens à cela (la singularité n'est pas un "lieu").

Tu m’étonnes… !??

Une « singularité » est un point se trouvant à l’extrémité de courbes mathématiques infinies. Courbes qui sont d’ailleurs définies par une théorie non adaptée.

Mais bon, si cela a un sens pour certains, je les envie, car pour moi c’est un constat que l’on met des mots qui ne veulent rien dire sur un « endroit » TOTALEMENT inconnu, qui pourrait très bien être régit par des lois physiques différentes de celles qui régissent notre univers, d’où mon terme de « ailleurs ».

[noir_ecaille]

Dire en topologie qu'une singularité serait "un lieu" même "ailleurs" revient par exemple en algèbre à parler de l'infini comme un nombre fini

[invitee6f0086a]

Dire en topologie qu'une singularité serait "un lieu" même "ailleurs" revient par exemple en algèbre à parler de l'infini comme un nombre fini

Oui !

Petite précision, j’assimilais par « ailleurs » une topologie régit par des lois physiques différentes.

Mais je suis très loin des connaissances des scientifiques, je n’emploi peut-être pas les termes adaptés.

[Amanuensis]

Petite précision, j’assimilais par « ailleurs » une topologie régit par des lois physiques différentes.

Différentes de quoi?

Et ensuite, c'est trop général, et du coup de la "spéculation non basée". Et donc hors domaine scientifique, et donc hors charte.

[Nicophil]

Bonjour,

on met des mots qui ne veulent rien dire sur un « endroit » TOTALEMENT inconnu, qui pourrait très bien être régit par des lois physiques différentes de celles qui régissent notre univers, d’où mon terme de « ailleurs ».

Des lois physiques différentes de celles qui régissent le reste de l'univers : "ailleurs que dans le reste" donc.

[invitee6f0086a]

Ben, dès qu’on parle de l’intérieur d’un trou noir, on est forcément dans le n’importe quoi ! dans la "spéculation non basée", et cela à tout niveau.

On n’a aucune information remontante, rien de chez rien, on est dans un raisonnement délirant qui n’a, par définition, rien de scientifique.

C’est tout simplement ça que je voulais exprimer, mais bon, si il y a des spécialistes de l’intérieur des trous noirs…

Et quand je lis ça :

Pour la singularité faut parler d'une trajectoire particulière, et il n'y en pas qu'une.

On parle de quoi ?

De la trajectoire de la matière qui « tombe » ? Ou de trajectoires mathématiques inappropriées dans cet environnement ?

Quand à ça :

Différentes de quoi?
Et ensuite, c'est trop général, et du coup de la "spéculation non basée". Et donc hors domaine scientifique, et donc hors charte.

Le fait même de spéculer de l’intérieur d’un trou noir est non scientifique, et donc hors chartre.

Mais bon, si je remplace mon « ailleurs » par « quelque part de bizarre», ça vous va ? c’est pas plus con que « singularité » qui définit un « machin » dont on n’a aucune idée.

[Nicophil]

Mais l'horizon, c'est la limite où s'arrête l'extérieur et où commence l'intérieur.
C'est la limite entre l'ailleurs et le reste.
Où est la limite de l'ailleurs ? Pas à l'intérieur de l'ailleurs !

[invitee6f0086a]

Mais l'horizon, c'est la limite où s'arrête l'extérieur et où commence l'intérieur.
C'est la limite entre l'ailleurs et le reste.
Où est la limite de l'ailleurs ? Pas à l'intérieur de l'ailleurs !

Oui, je sais, je ne comprends pas bien ce que tu veux dire.

Mon ailleurs ou bizarre commencerait juste après l’horizon.

[Deedee81]

Salut,

Ces questions/interrogations/critiques sur la physique au-delà de l'horizon sont une bouteille à encre sur Futura. On en a déjà discuté plusieurs fois.

Je dirai juste ceci :
- La physique décrivant les trous noirs et donc leur horizon et leur intérieur, c'est la relativité générale
- celle-ci est bien validée dans un domaine de conditions physiques déjà fort large
- les conditions physiques locales près de l'horizon d'un trou noir, même à l'intérieur, ne sont guère si exotiques. Surtout pour un trou noir super massif où les forces gravitationnelles à l'horizon sont plus faibles que sur Terre !!!!
- ce n'est que près du centre que les conditions physiques deviennent telles que la relativité générale est non validée et même fausse (on entre dans le domaine où la physique quantique intervient)
- on peut donc dire que même sous l'horizon les lois de la physique devraient être les mêmes
- ceci dit, difficile d'aller vérifier, ce qui est toujours gênant en physique. Mais personne n'a vérifier que les pommes tombaient bien vers le bas à la surface de Pluton, et je n'ai jamais vu un seul message sur Futura disant que la physique sur Pluton est différente. Il faut quand même faire une certaine confiance aux théories, du moins celles qui sont validées
- on peut aussi appeler l'intérieur d'un trou noir un "ailleurs", ce n'est qu'un nom et bien entendu la physique ne se fait pas à coup de vocabulaire . Cette zone est bien définie. Penrose attribue aussi aux différentes zones et frontières des symboles précis du genre i+, i-, I+, I-.... Les diagrammes de Penrose sont d'ailleurs un outil simple, visuel et très pratique pour visualiser des espaces-temps mêmes complexes (et pas seulement ceux des trous noirs). Je les conseille. Je les décrit ici : http://fr.scribd.com/doc/204166860/V...es-etoiles-pdf (curieusement j'ai des références sur de bonnes explications techniques mais à part ce document que j'ai écrit, je n'ai jamais vu de bonne vulgarisation de ces diagrammes. J'ai donc essayé de faire de mon mieux).

[inviteec0d6e6f]

Quand on veut mettre la charrue avant les bœufs, on passe 4 ans a ressasser toujours les mêmes questions sans jamais comprendre les réponses.
4 ans déjà, et pas le moindre progrès de compréhension de ces phénomènes, et toujours exactement les mêmes questions.
Ça peut durer 10 ans 100 ans 1000 ans si tu pouvais vivre jusque la, daniel100...
Il serait peut-être temps que tu commence a poser des questions dont tu peux comprendre les réponses, non ?
Exactement ce que je t'ai dit il y a déjà 4 ans de ça, tu m'avais alors snobé (pour ne pas dire "envoyé chier"), mais je constate que tu n'as pas progressé d'un misérable iota depuis.
Ni dans tes questions, ni dans ta compréhension des réponses.
Étourdissant... et pourtant si prévisible et si prévenu...
C'est pas faute de t'avoir mis en garde...
L'illustration typique du proverbe : "on ne fait pas boire un âne qui n'a pas soif"

Avant de tenter de comprendre les singularités des lois de notre physique, essayes déjà de comprendre ce que disent nos lois physiques pour des environnements non exotiques, de cette façon, tu apprendras enfin quelque chose de concret et on n'aura pas a relire encore et toujours les mêmes questions de ta part pendant les 4 années a venir.

Ben, dès qu’on parle de l’intérieur d’un trou noir, on est forcément dans le n’importe quoi !

Ha si ! Finalement, t'as appris un truc en 4 ans !
Ce qui ne t'empêches pas de remettre systématiquement le couvert sur ce sujet pourtant hors de ta portée...

[bb98]

Bonjour

Pour consoler notre ami à l'origine du fil, c'est un peu le syndrome pour toute encyclopédie, fusse t elle par "questions réponses" comme notre chère Futura : "à force de butiner, je ferai mon miel..."

Si les trous noirs intéressent, on se procure l'ouvrage de Luminet. Il est parfaitement accessible à tout honnête homme, même si quelques lignes de calculs peuvent échapper ; comme le dit si bien Alain Aspect, on saute ces lignes : "il n'est pas nécessaire de connaître le solfège pour apprécier la musique"

Quand l'ouvrage de Luminet aura été lu 2 ou 3 fois, alors, et SEULEMENT alors, on pourrait utilement poser 2 ou 3 questions sur les points qui seront, sûrement, resté obscures.

Voilà une proposition de démarche qui permettrait, à mon sens, de progresser. D'autres auront , forcément, d'autres avis.

Bonnes lectures

[noir_ecaille]

Un élément m'interpelle...

les conditions physiques locales près de l'horizon d'un trou noir, même à l'intérieur, ne sont guère si exotiques. Surtout pour un trou noir super massif où les forces gravitationnelles à l'horizon sont plus faibles que sur Terre !!!!

Que je comprenne... Il existe des cas où on pourrait théoriquement "marcher" à la surface de l'horizon des évènements (s'il était tangible) ? Eut égard qu'on marche à la surface de la Terre. Dans ce cas, pourquoi la lumière continue de tomber sans pouvoir s'échapper ?

[invitee6f0086a]

… tu m'avais alors snobé (pour ne pas dire "envoyé chier)…

HO !! j’ai fais ça moi, bizarre, tu es pourtant un être si délicieux et humble à lire.

Ha si ! Finalement, t'as appris un truc en 4 ans !

Ah ben tu vois, ça commence à rentrer.

[Amanuensis]

Je dirai juste ceci :
- La physique décrivant les trous noirs et donc leur horizon et leur intérieur, c'est la relativité générale
- celle-ci est bien validée dans un domaine de conditions physiques déjà fort large
- les conditions physiques locales près de l'horizon d'un trou noir, même à l'intérieur, ne sont guère si exotiques. Surtout pour un trou noir super massif où les forces gravitationnelles à l'horizon sont plus faibles que sur Terre !!!!
- ce n'est que près du centre que les conditions physiques deviennent telles que la relativité générale est non validée et même fausse (on entre dans le domaine où la physique quantique intervient)
- on peut donc dire que même sous l'horizon les lois de la physique devraient être les mêmes
- ceci dit, difficile d'aller vérifier, ce qui est toujours gênant en physique.

Je dirais tout simplement: la notion même de trou noir, et surtout ce qui se passe sous l'horizon, est de la spéculation fondée.

L'observation se limite à celle de zones "en effondrement inéluctable", l'horizon lui-même n'est pas observé et encore moins ce qu'il y a "derrière".

La plupart des (toutes les?) "spéculations fondées" (et celle-ci en particulier) sont des extrapolations de modèles, de modèles considérés comme valides dans d'autres conditions (c'est en cela qu'elles sont fondées), le "domaine de conditions physiques fort large".

La conséquence de cela est qu'en discuter demande de discuter le modèle, et donc de bien le connaître (et mieux que pour juste le comprendre pour sa relation avec l'effectivement observé).

La notion de trou noir est une "spéculation fondée" fondée sur la relativité générale. Dire que l'intérieur ne respecte par la RG est totalement ridicule, puisque la notion même d'intérieur de trou noir est extrapolée de la RG.

-----------

On constate un cheminement intellectuel finalement assez curieux. On part d'observations dont la plupart peuvent s'exprimer en "langage commun", on en tire un modèle rendant compte de ces observations là ; ensuite, on "joue" avec le modèle, en en tirant des extrapolations ("spéculations fondées") sur des phénomènes non observés et même non observables. On devrait s'arrêter là, et voir cela pour ce que c'est: un travail sur le modèle. Mais non, nombre(1) y veulent rajouter une couche et parler de ces extrapolations via le "langage commun". Et là ça dérape...

(1) Amateurs plus ou moins éclairés, journalistes, mais aussi professionnels cherchant à vulgariser, à se médiatiser.

[invitee6f0086a]

Je dirais tout simplement: la notion même de trou noir, et surtout ce qui se passe sous l'horizon, est de la spéculation fondée.

L'observation se limite à celle de zones "en effondrement inéluctable", l'horizon lui-même n'est pas observé et encore moins ce qu'il y a "derrière".

La plupart des (toutes les?) "spéculations fondées" (et celle-ci en particulier) sont des extrapolations de modèles, de modèles considérés comme valides dans d'autres conditions (c'est en cela qu'elles sont fondées), le "domaine de conditions physiques fort large".

La conséquence de cela est qu'en discuter demande de discuter le modèle, et donc de bien le connaître (et mieux que pour juste le comprendre pour sa relation avec l'effectivement observé).

La notion de trou noir est une "spéculation fondée" fondée sur la relativité générale. Dire que l'intérieur ne respecte par la RG est totalement ridicule, puisque la notion même d'intérieur de trou noir est extrapolée de la RG.

-----------

On constate un cheminement intellectuel finalement assez curieux. On part d'observations dont la plupart peuvent s'exprimer en "langage commun", on en tire un modèle rendant compte de ces observations là ; ensuite, on "joue" avec le modèle, en en tirant des extrapolations ("spéculations fondées") sur des phénomènes non observés et même non observables. On devrait s'arrêter là, et voir cela pour ce que c'est: un travail sur le modèle. Mais non, nombre(1) y veulent rajouter une couche et parler de ces extrapolations via le "langage commun". Et là ça dérape...

(1) Amateurs plus ou moins éclairés, journalistes, mais aussi professionnels cherchant à vulgariser, à se médiatiser.

Voila une réponse (avec celle de Deedee) plus instructive et intéressante que celle du message #13, merci !

[Deedee81]

Salut,

aussi pour cet excellent complément d'Amanuensis.

On constate un cheminement intellectuel finalement assez curieux. On part d'observations dont la plupart peuvent s'exprimer en "langage commun", on en tire un modèle rendant compte de ces observations là ; ensuite, on "joue" avec le modèle, en en tirant des extrapolations ("spéculations fondées") sur des phénomènes non observés et même non observables. On devrait s'arrêter là, et voir cela pour ce que c'est: un travail sur le modèle. Mais non, nombre(1) y veulent rajouter une couche et parler de ces extrapolations via le "langage commun". Et là ça dérape...

On constate ça dès qu'une situation de ce type peut se présenter. Par exemple en cosmologie.
Ou en gravitation quantique (mais moins dans ce domaine, sans doute à cause de sa technicité qui la rend difficile compréhensible par des, par exemple, journalistes. Mais ça existe quand même. Je potasse pas mal la gravité quantique à boucles et maintenant je me rend compte que certains articles de vulgarisation que j'ai lu n'étaient pas terrible. Pourtant certains avaient été écrit par un des théoriciens du domaine que j'apprécie beaucoup même quand "il parle en prose". Je ne donnerai pas son nom).

[Amanuensis]

Mouais... Encore quelque et je vais commencer à essayer de comprendre comment mon texte a pu être compris d'une manière si différente de celle visée.