Synchronisation d'horloges dans un univers en expansion.

[Zefram Cochrane]

Bonjour,

J'ouvre ce fil pour me familiariser avec les calculs en cosmologie (Je n'ai que des connaissance très parcéllaires c'est pour ça que je n'interviens pas en général sur ce sujet).

Pour le mégaparsec on prendra comme valeur SVP : Mpc=100 000 000 000 000 s.l
Pour la vitesse de Hubble Vo=70km/s/Mpc mais on pourra en prendre une plus grande dans les applications numériques si nécessaire.

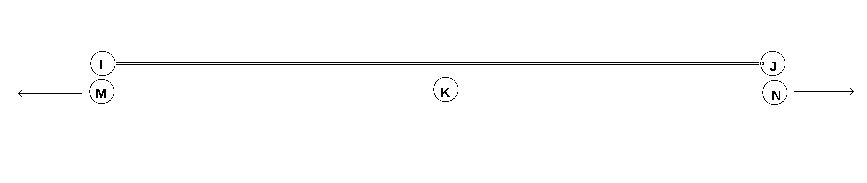
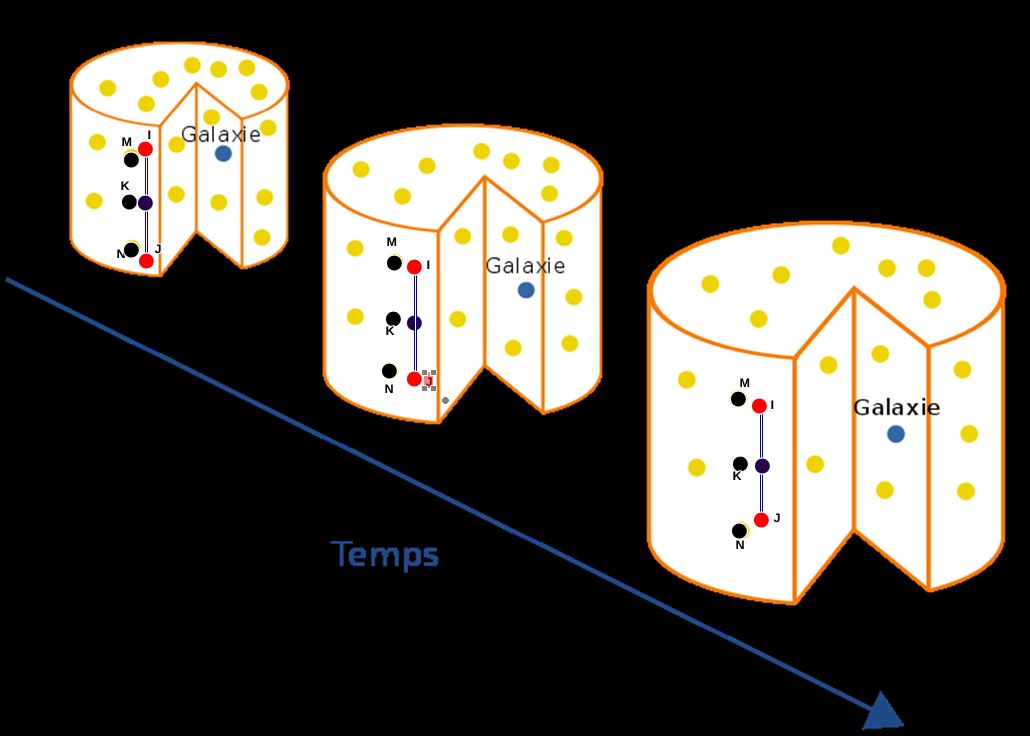
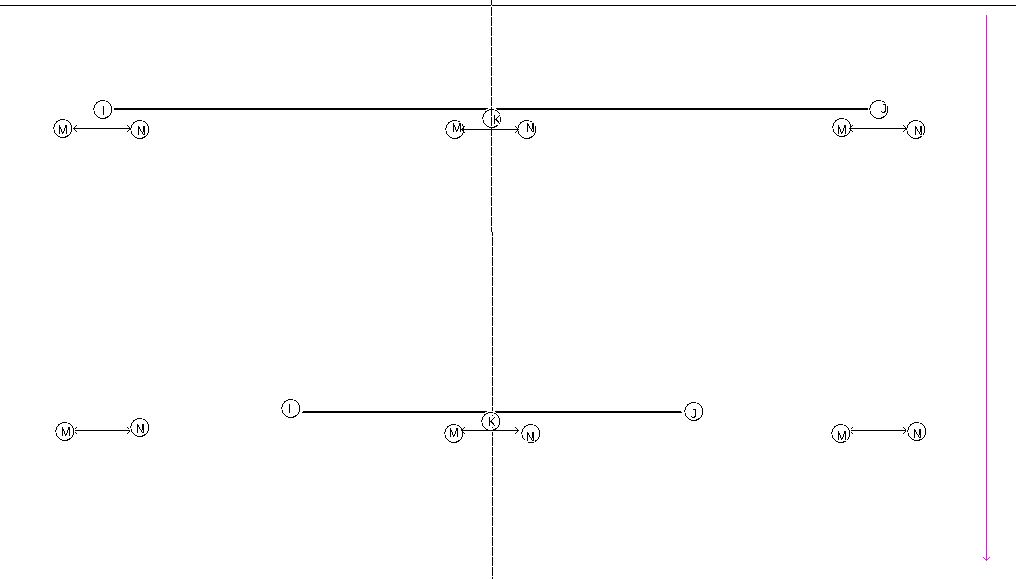
Soit I (observateur O) et J (observateur Q)deux bouées distantes reliées entre elle par une corde rigide de Ls.l de longueur. Q veut synchroniser son horloge sur celle de O
Théoriquement il verra que I et J battent le même rythme.
Donc il lui faut déterminer la distance L qui sépare I et J et pour cela il va envoyer un signal à O qui le réfléchira grâce à un miroir.

Et c'est là que les choses se compliquent parce que dans un univers en expansion, les photons sont retardés car la distance qu'ils auront à parcourir est >L. Donc, à la réception, Q verra son signal deux fois redschifté et globalement je peux écrire qu'entre l'instant d'émission et de réception avec c'<c .

Comment calculer c' en f° du redschift? comment calculer c' en fonction de L?

Merci de vos réponses.
-----

[Amanuensis]

Commencer par préciser les mouvements (ce qui demande usuellement de choisir un référentiel, ou mieux un système de coordonnées, pour les décrire, merci de le faire explicitement).

[Zefram Cochrane]

Salut,


J'ai fait un schéma pour clarifier la problématique.
K est au milieu de M et N. Du fait de l'expansion M et N vont s''écarter de K avec une vitesse comobile. La corde reliant I et J empêche I et J de s'écarter de K.
Par contre les signaux lumineux émis par I et J ""devraient"" subir les effets de l'expansion et donc être ""redschiftés"".

J'espère que la problématique est assez explicite et je crois que définir de manière pertinente le système de coordonnées fait partie de la solution du problème; d'où le besoin d'aide.

[Nicophil]

Bonjour,

Théoriquement il verra que I et J battent le même rythme.

Je ne crois pas qu'on puisse dire ça...
On se sert des supernovae comme horloges standardisées mais elles apparaissent ralenties : plus on regarde loin, plus elles semblent évoluer au ralenti : leur période de référence (la seconde) semble dilatée en 1+z.

[A voir en vidéo sur Futura]

[papy-alain]

Bonjour,

Je ne crois pas qu'on puisse dire ça...
On se sert des supernovae comme horloges standardisées mais elles apparaissent ralenties : plus on regarde loin, plus elles semblent évoluer au ralenti : leur période de référence (la seconde) semble dilatée en 1+z.

C'est effectivement le cas pour M et N, dans l'exemple de Zefram.
Mais pour I et J ?

[Amanuensis]

J'ai fait un schéma pour clarifier la problématique.

??

K est au milieu de M et N. Du fait de l'expansion M et N vont s''écarter de K avec une vitesse comobile. La corde reliant I et J empêche I et J de s'écarter de K.

Hmm.. C'est le contraire j'imagine: M et N ont une vitesse comobile nulle, alors que la corde reliant I et J leur impose une vitesse comobile non nulle?

J'espère que la problématique est assez explicite et je crois que définir de manière pertinente le système de coordonnées fait partie de la solution du problème

Certainement pas. Dans l'état on est obligé de deviner de quels mouvements il s'agit: un modèle LFRW (ou plus précis?), K (= milieu de la ficelle), N et M en chute libre, I et J de mouvement contraint par l'existence de la ficelle. Et d'autres détails comme l'absence de rotation, une certaine symétrie entre I et J, etc.

Et ces différents points affectent tous la réponse.

Le première "aide", comme très souvent en physique, consiste à aider à ce que la question soit suffisamment formalisée pour pouvoir être traitée avec les moyens mathématiques proposés par les théories en vigueur.

[Et au bout d'un certain temps cela devient chiant d'avoir à le faire pour toujours les mêmes, qui préfèrent lancer des questions vagues répétitivement plutôt qu'apprendre des discussions précédentes.]

[Mct92mct]

Salut,
Pièce jointe 325887

J'ai fait un schéma pour clarifier la problématique.
K est au milieu de M et N. Du fait de l'expansion M et N vont s''écarter de K avec une vitesse comobile. La corde reliant I et J empêche I et J de s'écarter de K.
Par contre les signaux lumineux émis par I et J ""devraient"" subir les effets de l'expansion et donc être ""redschiftés"".

J'espère que la problématique est assez explicite et je crois que définir de manière pertinente le système de coordonnées fait partie de la solution du problème; d'où le besoin d'aide.

Bonjour, qu'est ce qui te fait dire qu'une corde est capable d'empêcher I et J de s'écarter de K? et que l'expansion ne peut pas influer aussi sur les distances interatomiques de la corde surtout sur les distances que tu envisages?
Cordialement

[Amanuensis]

que l'expansion ne peut pas influer aussi sur les distances interatomiques de la corde

Il a précisé le taux d'expansion, et on sait qu'à ce taux-là elles ne sont pas affectées.

[Nicophil]

K est au milieu de M et N. Du fait de l'expansion M et N vont s''écarter de K avec une vitesse comobile.

Comme dit par Amanuensis, la définition de "distance comobile" est telle qu'elle reste constante malgré l'expansion.
Donc dans un système de coordonnées comobiles, M et N sont immobiles.

Et I et J sont en mouvement vers K. D'où, comme dit par papy-alain, un blueshift Doppler classique qui annule le redshift dû à l'expansion...

[Zefram Cochrane]

??

Et celui ci? Je l'ai tiré de https://fr.wikipedia.org/wiki/Expansion_de_l%27Univers#

Sur ce schéma, le shcéma que j'ai fait précédemment correspond à la situation du gâteau du milieu.
K reste au même niveau que le milieu de la corde que j'ai matérialisé par un point violet(le décalage latéral est pur rendre le schéma lisible). La longueur L séparant I de J reste invariante, M et N s'écartent.

Hmm.. C'est le contraire j'imagine: M et N ont une vitesse comobile nulle, alors que la corde reliant I et J leur impose une vitesse comobile non nulle?

Si comme le dit Nicophil, la distance comobile entre M et N ne varie pas du fait de leur vitesse comobile nulle, cela ne veut il pas dire que la longueur ( comobile ?) de la corde L se réduit au fil du temps (cosmique?) ?

Certainement pas. Dans l'état on est obligé de deviner de quels mouvements il s'agit: un modèle LFRW (ou plus précis?), K (= milieu de la ficelle), N et M en chute libre, I et J de mouvement contraint par l'existence de la ficelle. Et d'autres détails comme l'absence de rotation, une certaine symétrie entre I et J, etc.

Et ces différents points affectent tous la réponse.

Le première "aide", comme très souvent en physique, consiste à aider à ce que la question soit suffisamment formalisée pour pouvoir être traitée avec les moyens mathématiques proposés par les théories en vigueur.

I et J sont stationnaires, pas de rotation ils voient le CMB isotrope à T°=2.728°K.

[Et au bout d'un certain temps cela devient chiant d'avoir à le faire pour toujours les mêmes, qui préfèrent lancer des questions vagues répétitivement plutôt qu'apprendre des discussions précédentes.]

Je pose très rarement des question à propos du modèle LFRW

[Zefram Cochrane]

Et I et J sont en mouvement vers K. D'où, comme dit par papy-alain, un blueshift Doppler classique qui annule le redshift dû à l'expansion...

En mouvement comobile donc.
J'ai une question justement par rapport au blueschift. Sauf erreur de ma part, la tension de la corde engendrée par l'expansion est homogène en tout point de la corde et c'est d'ailleurs pour cela que je m'étais gardé de représenter le milieu de la corde sur mon premier schéma. Peut on faire un lien entre cette tension (accélération g) et l'horizon de Rindler c²/g?
Si I accélère vers J et vice versae en considérant M et N fixes en coordonnées comobiles , I et J verraient l'autre blueschifté du fait de leur vitesse comobile relative mais qui serait annulé par le redschift du à l'expansion si j'ai bien compris?
(cela expliquerait que Q au niveau de J voit l'horloge I battre le même rythme).

Par contre reste peut-être le problème des photons lumineux qui progressant dans un espace en expansion ne parcourent pas L à c?

[Amanuensis]

En mouvement comobile donc.
J'ai une question justement par rapport au blueschift. Sauf erreur de ma part, la tension de la corde engendrée par l'expansion est homogène en tout point de la corde

Sous hypothèse de masse de corde nulle, peut-être.

et c'est d'ailleurs pour cela que je m'étais gardé de représenter le milieu de la corde sur mon premier schéma. Peut on faire un lien entre cette tension (accélération g)

La tension n'est pas une accélération.

Si I accélère vers J et vice versae en considérant M et N fixes en coordonnées comobiles , I et J verraient l'autre blueschifté du fait de leur vitesse comobile relative mais qui serait annulé par le redschift du à l'expansion si j'ai bien compris?

C'est ce que quelqu'un a écrit. Mais une simple considération de symétrie amène à la conclusion que I et J sont synchronisables, sans avoir à réfléchir ou affirmer quoi que ce soit sur des décalages virtuels.

[Nicophil]

Par contre reste peut-être le problème des photons lumineux qui progressant dans un espace en expansion ne parcourent pas L à c?

La vitesse des photons est indépendante de la vitesse de l'horloge émettrice...

Rentre différentes valeurs de z dans le calculateur de Ned Wright : http://www.astro.ucla.edu/~wright/CosmoCalc.html pour voir comment évoluent les différents concepts de distance.
Par exemple, pour z = 0.5 :
- la distance à l'émission (distance angulaire) était 4.2 Gal.
- l'émission a eu lieu il y a 5.1 milliards d'années, c'est la durée du voyage du photon (distance de lookback time).
- on réceptionne aujourd'hui le photon, la galaxie est désormais à 6.2 Gal (distance comobile).

[Zefram Cochrane]

Bonjour,
je voudrais savoir si à T=0s J émet un signal vers I muni d'un miroir si je peux écrire que L=T*c/2
c la vitesse de la lumière du vide et T la durée de l'aller-retour du signal?

[Amanuensis]

Et L serait quoi? (Question faussement naïve...)

[Amanuensis]

À part le cas trivial de définition de L, le calcul n'est pas trivial, il me semble qu'il faut résoudre une équation qui n'a de solution explicite que pour certaines fonctions d'échelle. Et encore.

[Amanuensis]

Proposition de recette (à confirmer, infirmer, améliorer, etc.) :

1- Choisir les coordonnées comobiles avec t=0 pour le départ du rayon en I, avec a(t=0)=1 et avec comme mouvement de K t --> (t,0) ;
2- Exprimer le mouvement de J dans le système de coordonnées ;
3- Exprimer le mouvement du rayon t --> x(t), contraint par x(0)=0 et dt = a(t)dx
4- Trouver le point d'intersection des deux mouvements, ce qui donne T ;
5- Appliquer la définition choisie pour L pour vérifier la proposition.

[Nicophil]

Rentre différentes valeurs de z dans le calculateur de Ned Wright : http://www.astro.ucla.edu/~wright/CosmoCalc.html

Je me suis amusé à mettre la densité de matière à 0.45, dans un Univers "flat".
Pour z = 1 :
- la distance à l'émission (distance angulaire) était 5 Gal.
- l'émission a eu lieu il y a 7.2 milliards d'années, c'est la durée du voyage du photon (distance de look back time).
- on réceptionne aujourd'hui le photon, la galaxie est désormais à 10 Gal (distance comobile).

Pendant la durée du voyage, la distance a doublé (taux de 100%). Elle augmente (aujourd'hui ?) d'une seconde-lumière par seconde. Ainsi, les photons émis à intervalle d'une seconde arrivent à intervalle de deux secondes.
Il aurait fallu qu'à l'époque la galaxie vienne vers la Voie lactée à quasiment c pour quasi-compenser ; oui mais alors il y a le redshift RR...

[Nicophil]

Pendant la durée du voyage, la distance a doublé (taux de 100%).

C'est cette distance qui est appelée "distance propre".

[Amanuensis]

C'est cette distance qui est appelée "distance propre".

De la prégnance d'un temps unique...

Marrant de réaliser dans ces messages toutes les conventions implicites, dont le côté "naturel" ne saurait être mis en doute.

[Zefram Cochrane]

La longueur de la corde tendue entre I et J.
Pour moi c'est oui. Mais je voudrais qu'on me confirme.

[Zefram Cochrane]

Pourrais-tu m'expliquer ton message de 20h19 STP?

[Zefram Cochrane]

J'essaierai de proposer un truc en tenant compte du message de 20h26.

[Nicophil]

toutes les conventions implicites

Tant que ça ? quelle est la principale ?

[Mailou75]

A supposer que l'expansion est préexistante a l'expérience.
Alors l'observateur central en K, au moment ou il voit apparaître la corde en I et J, voit aussi le redshift des galaxies I et J augmenter moins rapidement.
En effet, les galaxies M et N subissent un redshift lié a la vitesse de variation du facteur d'échelle ET au temps de parcours du photon.
L'observateur percevra donc deux nuances entre les galaxies attachées et libres :
- les galaxies attachées aurons désormais une Da (angulaire)fixe
- leur redshift sera moins important que les galaxies libres
uniquement du au fait que la lumière voyagera moins longtemps (puisqu'elles sont plus pres)
et que donc à réception me facteur d'échelle aura "moins évolué"

(On peut en plus considérer que le vide en expansion va ralentir/faire reculer le photon, mais la je vais laisser les personnes qui y croient t'en parler..)

bon courage
Mailou

[Zefram Cochrane]

Salut,


J'ai essayé de progresser un peux , au dessus ce sont les positions des M ( i,k,j) et N (i,k,j) par rapport à I K J et en dessous les positions des même points quand les distances comobiles ( en prenant la longueur de la corde L constante) ont doublé au bout d'un temps T matérialisé par la flèche de droite.

Question : est ce que ce temps T correspond à la durée coordonnée du référentiel de I K et J (I K et J étant des observateurs inertiels)
Puis je dire que la vitesse de la lumière est constante le long de la corde dans le sens qu'un signal lumineux envoyé par J vers I lui reviendra au bout d'un temps T = T(j->k) + T(k->i)+T(i->k)+T(k->j) ?

[Amanuensis]

du référentiel de I K et J (I K et J étant des observateurs inertiels)

C'est quoi "le" référentiel "de" I K et J?

En RG il n'y a pas de définition implicite d'un référentiel associé à un ou plusieurs "points". Faut toujours définir précisément de quoi il est question.

À ce qu'on peut comprendre, "T" réfère à une durée comobile, i.e., à la coordonnée temporelle d'un système de coordonnées comobile (coordonnée définie à une constante additive et à l'unité près). Le coordonnée temporelle comobile est un temps propre pour tout mouvement "comobile", c'est à dire de coordonnées spatiales comobiles constantes, = tout mouvement immobile relativement au référentiel comobile. Et ces mouvements sont inertiels (= chute libre).

Puis je dire que la vitesse de la lumière est constante le long de la corde dans le sens qu'un signal lumineux envoyé par J vers I lui reviendra au bout d'un temps T = T(j->k) + T(k->i)+T(i->k)+T(k->j) ?

Que signifie "le long de la corde"? Le signal lumineux est transporté dans une fibre optique le long de la corde?

[Amanuensis]

Pour le diagramme, quelle est la coordonnée "horizontale" (la verticale est le temps comobile, a priori)?


[Si c'était une coordonnée spatiale comobile, M et N restent à distance (différence de coordonnée spatiale) constante, et la distance (tj au sens de la différence de coordonnées) entre I et J devrait être divisée par 2.

Cela ressemble plutôt à un système de coordonnées tel que la coordonnée spatiale est y=a(t)x, avec x la coordonnée spatiale comobile.]

[Zefram Cochrane]

Si je remplace la corde par un tube creux et que J envoie vers I un faisceau laser dans le tube; il ne devrait pas y avoir de grosse différence su J envoie un faisceau laser qui se propage vers I en suivant la paroi externe de la corde ( si on néglige l'expansion latérale) ? Si?

En reprenant ta définition et en reprenant mon schéma
Si T est la durée comobile , ce serait a durée propre écoulée pour les corps Mi ; Ni ; Mk; Nk ; Mj ; Nj et K qui gardent la même position relative entre eux ( mouvement immobile relativement au référentiel comobile).

K étant immobile par rapport à I et J ; T n'est il pas la durée propre écoulée pour I et J?

[Zefram Cochrane]

Pour le diagramme, quelle est la coordonnée "horizontale" (la verticale est le temps comobile, a priori)?


[Si c'était une coordonnée spatiale comobile, M et N restent à distance (différence de coordonnée spatiale) constante, et la distance (tj au sens de la différence de coordonnées) entre I et J devrait être divisée par 2.

Cela ressemble plutôt à un système de coordonnées tel que la coordonnée spatiale est y=a(t)x, avec x la coordonnée spatiale comobile.]

C'est ça , j'ai fait eprès de garder les distances entre les M(i;j;k) et N(i;j;k) constants j'ai divisé la longueur ( comobile ? ) L ( que tu as appelée tj) entre I et J par 2. Bien évidement si la corde (tube) est graduée, pour I et J la longueur L ne varie pas.