Bonjour,
Je me suis posé la question suivante cette nuit.
Dans le raisonnement suivant, il faut garder en tête que ce n'est qu'une analogie à N-1 dimensions spatiales par rapport au nombre de dimensions de l'espace constituant (l'espace-temps de) l'Univers observable. En effet, l'Univers a 3 dimensions spatiales, et non 2 comme sur la surface d'une 2-sphère. Mais c'est un peu plus difficile de concevoir la surface d'une 3-sphère...
On observe que la courbure de l'univers observable est nulle (la géométrie de l'espace est euclidienne).
Il y a deux possibilités :
- Soit la courbure de l'univers entier est nulle
- Soit la courbure de l'univers entier est positive (géométrie sphérique) ou négative (géométrie hyperbolique), mais le rayon de courbure est tellement grand que l'univers observable (la région voisine de la voie lactée = dans un rayon de 13,7 années-lumières) semble plat.
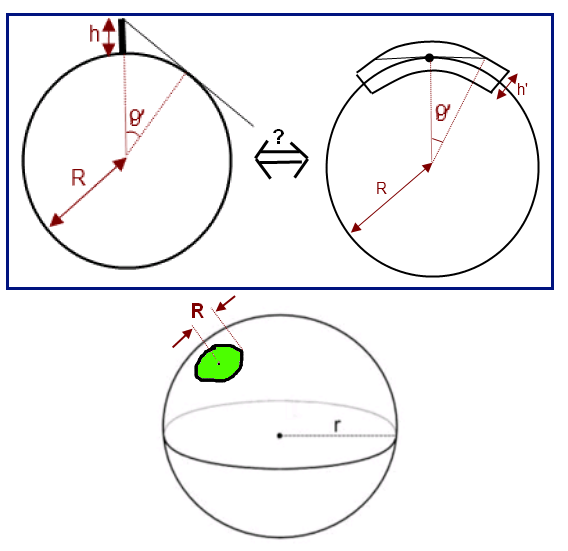
Prenons le cas où la courbure est positive, et faisons l'analogie avec quelqu'un au sommet d'un mât de bateau qui observe l'horizon terrestre.
On peut facilement calculer que la distance (ou l'anglequi la sous-tend) jusqu'à laquelle il ne pourra plus rien voir, dépend de la hauteur du mât, et du rayon de courbure de la Terre.
Je ne sais pas exactement à quoi correspond "la hauteur du mât" dans cette analogie d'une 2-sphère plongée dans un espace euclidien à 3 dimensions...
Dans l'encadré bleu de l'image attachée, est-ce que l'analogie présentée est mathématiquement plausible? (on donne une "épaisseur" à la distribution de matière (censée être à la surface), tout comme le mât s'extrait de la surface...
Dans ce cas, ne pourrait-on pas relier la quantité de matière visible (les étoiles :) dans l'univers observable par rapport à la quantité de matière totale attendue (depuis les mesures faites des oscillations acoustiques du CMB :
), à la surface de la région de l'univers observable (le disque vert de rayon R sur le dessin) par rapport à la surface totale de l'univers (sphère de rayon r sur le dessin).
Pour illustrer, grossièrement, faire quelque chose du genre :
Ma question générale est :
Est-ce que ce genre de considérations sont de l'ordre du farfelu, ou de l'ordre de l'envisageable...il y a-t-il des soupçons de plausibilité dans le raisonnement présenté? Il y a-t-il des contradictions avec les observations?
Je vous remercie d'avance pour vos interventions
-----