Rs = Horizon des evènements pour qui ?

[Mailou75]

Bonjour a tous,

Quelque chose me dérange dans la valeur que l'on fixe pour l'horizon des évènements d'un trou noir de Schwarzschild, le fameux Rs.
Je ne comprends pas pourquoi cette valeur est conservée pour tout observateur alors qu'elle devrait justement dépendre de la position de celui ci.
J'avais déjà abordé le sujet mais je vais essayer de décrire plus amplement ce que je comprend et j'aimerais beaucoup avoir vos critiques sur l'erreur dans le raisonnement...

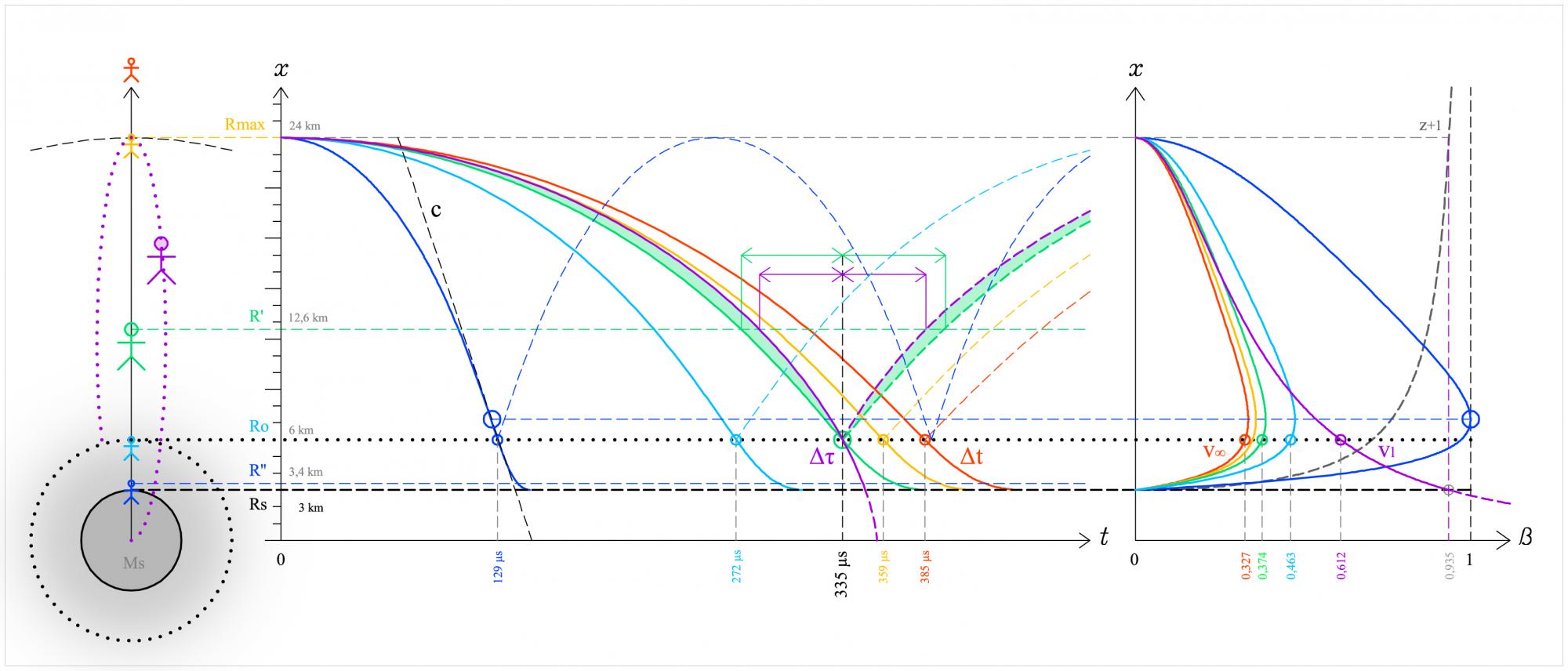
Prenons un trou noir de masse M, son Rs vaut 2GM/c², par définition.
Ce qui signifie que la vitesse de libération (radiale) depuis r=Rs vaut c, car V(r)=racine(2GM/r)=c
Jusqu'ici rien de neuf...

Mais voilà comment j'interprète la solution de Schwarzschild :
Si on parle d'un objet ayant une masse, alors la vitesse de libération ~c en Rs lui permettra d'atteindre l'infini avec une vitesse nulle.
Si on parle d'un photon, alors sa vitesse c en Rs lui permettra d'atteindre l'infini avec un redshift infini, ce qui se trouve en dessous de Rs est invisible.
Ceci est vrai pour l'observateur à l'infini, celui de Schwarzschild et numériquement on peut assimiler tout observateur à plus de 100Rs (c'est peu) comme étant à l'infini.

Maintenant supposons que la vitesse en Rs soit inférieure à c :
Si on parle d'un objet ayant une masse, alors la vitesse v en Rs lui permettra d'atteindre une "altitude" (distance depuis le centre) R' avec une vitesse nulle. (R'=Rs²)
Si on parle d'un photon, de vitesse c, alors il atteindra l'altitude R' avec un redshift inférieur à l'infini, il sera visible !

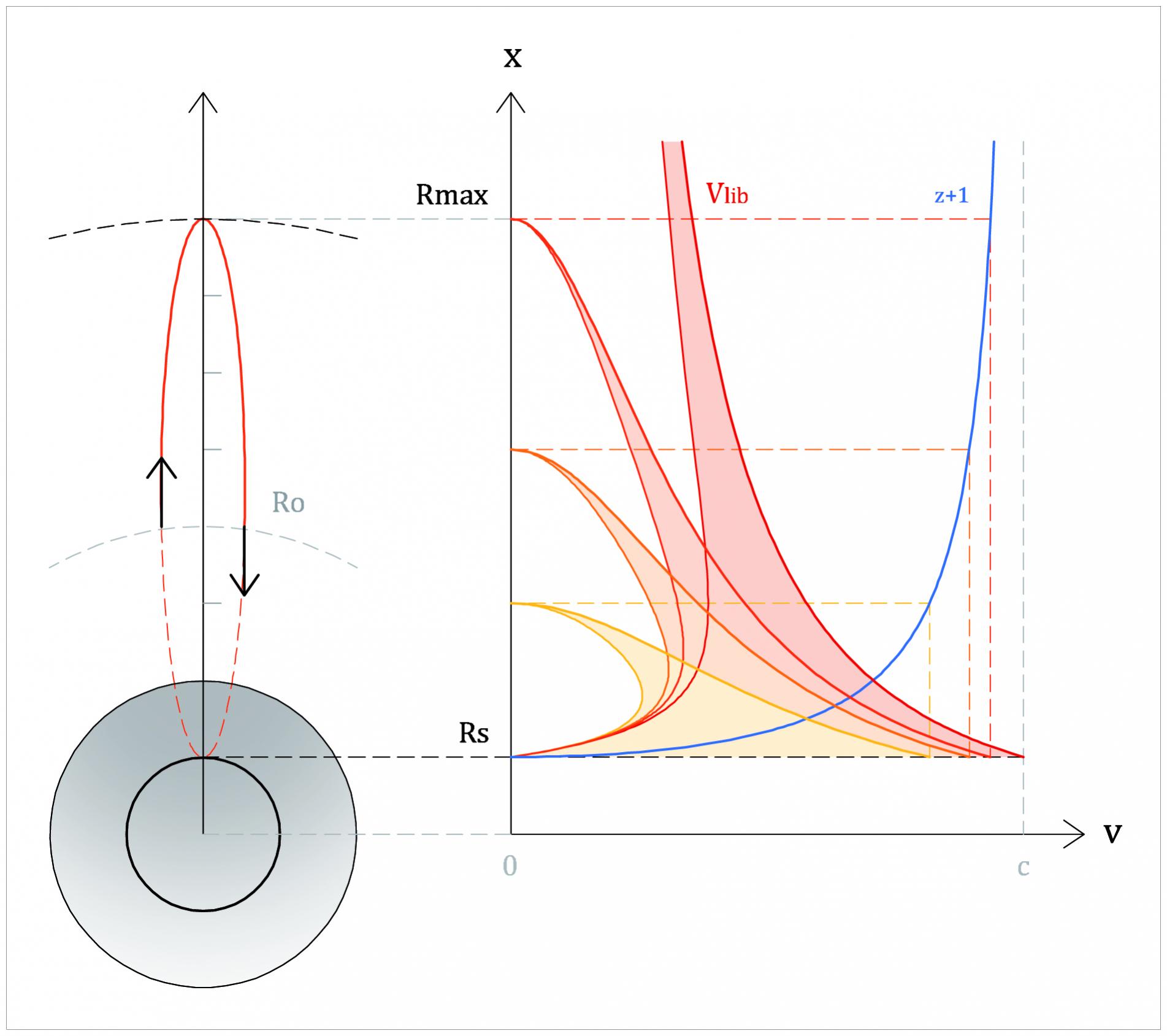
Et supposons que la vitesse au passage en Rs voit v mais que l'objet soit parti à c depuis une altitude Ro inférieure à Rs
Si on parle d'un objet ayant une masse, alors la vitesse c en Ro lui permettra d'atteindre Rs avec une vitesse v, etc... (voir précédemment)
Si on parle d'un photon, de vitesse c, alors il atteindra l'altitude Rs déjà redshifté puis arrivera en R' avec un redshift infini !

Ce qui veut dire que dans le dernier cas, un observateur en R' verrait tout ce qui se passe entre Rs et Ro !!
Donc d'une part ça veut dire que l'horizon dépend de l'observateur : Rs pour celui à l'infini mais Ro pour celui en R'
Et que pour l'observateur en Rs le temps s'écoule au niveau de Rs mais plus en Ro, son horizon.

C'est un peu la même histoire que le redshift comparé à une "lumière lente", un objet à vitesse nulle (apoastre) vaut un redshift infini...
Cette vision se rapproche de l'horizon terrestre où le fait d'avancer vers l'horizon modifie ce dernier.

Voilà, merci à ceux qui m'ont lu et à ceux qui me répondront,
A+
Mailou
-----

[invite5418555b]

Salut Mailou,

JE NE SUIS PAS SUR, mais il me semble qu'il y a une confusion concernant ce qu'est la vitesse de liberation dans le cas d'un TN. On peut la calculer avec l'equation V(r)=racine(2GM/r), mais cela ne veut pas dire qu'il est possible de sortir de Rs. Il me semble que tous les cones de lumiere a partir de Rs pointent vers l'interieur, et donc qu'il est impossible de sortir.

Ce n'est pas la meme chose que dans une vlib classique ou on peut lancer un objet en l'air a une vitesse inferieur a vlib et l'objet monte puis redescend. J'ai l'impression que la difference vient du fait des phenomenes relativistes extremes qui se produisent a l'horizon.

Cela dit je ne suis pas sur et j'aimerais bien avoir plus d'explications aussi.

Nicolas.

[Amanuensis]

La méthode pour réponse à ce genre de question est de prendre l'équation des géodésiques et de la résoudre pour les données choisies.

Pour une trajectoire radiale, on a





avec epsilon=1 pour une masse non nulle, et 0 pour une masse nulle.

---

Pour l'application demandée, faudrait clarifier de quelle vitesse on parle, l'utiliser pour fixer E et en déduire la géodésique.

[Mailou75]

Merci à vous,

Il me semble que tous les cones de lumiere a partir de Rs pointent vers l'interieur, et donc qu'il est impossible de sortir.

C'est ce que j'essaye de comprendre... si on peut faire le parallèle entre l'apoastre d'une trajectoire pour un objet et un redshift infini, alors un observateur qui ne serait pas à l'infini verrait le temps s'écouler en Rs. Si un objet atteint une altitude R' en ayant une vitesse v en Rs, alors oui il est "impossible de s'en sortir" dans le sens "atteindre l'infini" sans avoir une vitesse c en Rs. (Ex : En ayant une vitesse de v=0,93c en Rs on atteint seulement R'=8Rs). Le parallèle suppose que pour un observateur en R' la lumière provenant de Rs n'ait pas un redshift infini, cad que le temps n'y est pas figé.

.......

La méthode pour réponse à ce genre de question est de prendre l'équation des géodésiques et de la résoudre pour les données choisies.

Pour une trajectoire radiale, on a





avec epsilon=1 pour une masse non nulle, et 0 pour une masse nulle.

Cooool !! ça n'a pas l'air trop sorcier vu comme ça, mais tu connais mon niveau en maths
Quelques précisions stp ...
d'est la longeur de ... ? Pour E je prend hv ou mv²/2 ou autre chose ? Mais comment ça s'utilise ce truc ?

Pour l'application demandée, faudrait clarifier de quelle vitesse on parle, l'utiliser pour fixer E et en déduire la géodésique.

Je ne sais pas... prenons un TN de masse solaire Rs~3km et un objet de 1Kg projeté à 24km (8Rs v=0,93c)
à comparer au redshift d'un rayon lumineux perçu par un observateur à 24km du centre du TN

Merci d'avance

[A voir en vidéo sur Futura]

[Amanuensis]

d'est la longeur de ... ?

C'est un paramètre affine. Le temps propre tau pour une masse non nulle, et n'importe quoi pour une masse nulle.

Pour E je prend hv ou mv²/2 ou autre chose ? Mais comment ça s'utilise ce truc ?

E c'est juste un paramètre distinguant différentes géodésiques, on peut l'interpréter comme une énergie dans le système de coordonnées de Schwarzschild.

Pour l'utiliser, faut choisir E. Typiquement en fixant la vitesse v en un point (t, r) on fixe E. Et yapuka exprimer toute la géodésique en intégrant les équations.

Pour les géodésiques lumière E intervient peu: la seconde équation donne dr/dlambda = +/- E (selon la direction), et la première vire à la fois E et dlambda pour donner dr/dt = (1-R/r)

Je ne sais pas... prenons un TN de masse solaire Rs~3km et un objet de 1Kg projeté à 24km (8Rs v=0,93c)
à comparer au redshift d'un rayon lumineux perçu par un observateur à 24km du centre du TN

La vitesse dans quel référentiel? Si c'est en coordonnées de Schw. (plus ou moins le référentiel à l'infini), cela veut dire que la vitesse est dr/dt.

[invite5418555b]

C'est ce que j'essaye de comprendre... si on peut faire le parallèle entre l'apoastre d'une trajectoire pour un objet et un redshift infini, alors un observateur qui ne serait pas à l'infini verrait le temps s'écouler en Rs. Si un objet atteint une altitude R' en ayant une vitesse v en Rs, alors oui il est "impossible de s'en sortir" dans le sens "atteindre l'infini" sans avoir une vitesse c en Rs. (Ex : En ayant une vitesse de v=0,93c en Rs on atteint seulement R'=8Rs). Le parallèle suppose que pour un observateur en R' la lumière provenant de Rs n'ait pas un redshift infini, cad que le temps n'y est pas figé.

Mais si il est possible a un objet de traverser Rs vers l'exterieur et de se rendre a l'altitude 8Rs, a cette altitude, vlib est inferieure a c, donc pourquoi ne serait-il pas possible a cet objet d'accelerer et de s'echapper definitivement du TN?

Aussi si l'objet emet de la lumiere, une fois qu'est est a une altitude superieure a Rs, vlib etant inferieure a c a partir de ce point, sa lumiere devrait etre capable de s'echapper definitement. L'objet, par contre, retomberait.

Cela voudrait dire qu'il est possible de s'echapper d'un TN, ce qui va a l'encontre de ce qui est communement admis ( a part de rayonnement de Hawking ).

Je me posais exactement le meme genre de question que tu te poses, mais je ne suis pas sur qu'il soit reellement possible de traverser Rs vers l'exterieur.

[Zefram Cochrane]

Bonjour,

Pour un observateur exterieur stationnaire au TN, la vitesse de la lumière coordonnée au niveau de Rs est nulle. La vitesse de libération est maximale à une certaine distance du TN (cela doit pouvoir se calculer) et correpond à un certain nombre de fois Rs. Un astronaute ne peut donc s'échapper du champ d'attraction du TN.

Pour l'astronaute comme pour un photon, au niveau de Rs, ils sont séparés de l'observateur externe stationnaire d'une distance infinie quelle que soit la distance à laquelle l'observateur stationnaire se trouve du centre du TN de son point de vue.

Il me semble qu'un observateur en chute libre est en apensanteur. Si sa vitesse de chute est v (de son point de vue) à une distance r, je ne sais pas si on peut appliquer le raisonnement dans le cas d'une ascension libre, puisqu'il n'est plus en apesanteur. Je ne pense pas que sa perception de l'espace-temps soit la même dans le cas de la chute libre ou de l'ascension libre.

Je suis quand même d'accord sur le point que Rs (en vertu de la RR) doit différer pour un observateur selon la distance qui le sépare du centre du TN. Par exemple si le Soleil devenait un TN on dit que son rayon serait de 3 Km (du point de vue de l'observateur à l'oo) mais dans l'absolu, je ne sais pas si cette valeur serait strictement la même si on est sur Terre ou sur Venus. cette vision doit aussi différer selon que l'observateur soit fixe ou en déplacement radial.

Cordialement,
Zefram

[Mailou75]

Merci à vous,

C'est un paramètre affine. Le temps propre tau pour une masse non nulle, et n'importe quoi pour une masse nulle.
E c'est juste un paramètre distinguant différentes géodésiques, on peut l'interpréter comme une énergie dans le système de coordonnées de Schwarzschild.
Pour l'utiliser, faut choisir E. Typiquement en fixant la vitesse v en un point (t, r) on fixe E. Et yapuka exprimer toute la géodésique en intégrant les équations.
Pour les géodésiques lumière E intervient peu: la seconde équation donne dr/dlambda = +/- E (selon la direction), et la première vire à la fois E et dlambda pour donner dr/dt = (1-R/r)

pas simple en fait...
Aurais tu le courage de faire un exemple chiffré, je ne vois pas trop comment utiliser tout ça...
quelles valeurs donner à E, R, s,t..., quelles sont les inconnues, etc ?
Une petite application numérique pourrait aider à saisir le sens de ce calcul

La vitesse dans quel référentiel? Si c'est en coordonnées de Schw. (plus ou moins le référentiel à l'infini), cela veut dire que la vitesse est dr/dt.

J'aurais dit dr/d la vitesse en coordonnées spatiales de Schwarzschild et en temps propre du voyageur.
Comme le dit Zef plus bas, la vitesse "coordonnée" est toujours nulle en Rs car elle tient compte du redshift gravitationnel.
Si je ne dis pas de c...
..........

a cette altitude, vlib est inferieure a c, donc pourquoi ne serait-il pas possible a cet objet d'accelerer et de s'echapper definitivement du TN?

C'est possible! mais tu parles d'accélérer au cours de l'expérience, c'est hors sujet. La lumière "n'accélère" pas, sauf si tu arrives à la blueshifter en route

Aussi si l'objet emet de la lumiere, une fois qu'est est a une altitude superieure a Rs, vlib etant inferieure a c a partir de ce point, sa lumiere devrait etre capable de s'echapper definitement.

Oui, tout ce qui gravite autour d'un TN (ou n'importe quoi) reste visible

Cela voudrait dire qu'il est possible de s'echapper d'un TN, ce qui va a l'encontre de ce qui est communement admis

Non
..........

Pour un observateur exterieur stationnaire au TN, la vitesse de la lumière coordonnée au niveau de Rs est nulle.

Vitesse coordonnée oui mais vitesse de la lumière non !?

La vitesse de libération est maximale à une certaine distance du TN (cela doit pouvoir se calculer) et correpond à un certain nombre de fois Rs. Un astronaute ne peut donc s'échapper du champ d'attraction du TN.

Correspond à un nombre fois Rs qui varie en fonction de la vitesse initiale ! voir graph http://forums.futura-sciences.com/as...ml#post4404078, pour Vlib on trouve deux courbes celle qui part à v=c (locale?) et celle qui part à v=0 (coordonnée, obs à l'infini), idem pour les V<Vlib on voit que le point d'inflexion dont tu parles est variable

Pour l'astronaute comme pour un photon, au niveau de Rs, ils sont séparés de l'observateur externe stationnaire d'une distance infinie quelle que soit la distance à laquelle l'observateur stationnaire se trouve du centre du TN de son point de vue.

Un effet de la dilatation de l'espace, au sens RR pas expansion ! Entre Rs et l'infini l'espace est "penché", deux points particuliers sur une courbe mais pas forcément assimilables à tous les observateurs (surtout ceux en dessous de 100Rs ou le delta dépasse 1%). Un horizon qui ne serait pas "matérialisé" mais une limite où les dimensions s'inversent, enfin c'est comme ça que je le vois...

Mailou

[Zefram Cochrane]

Je suis resté consensuel, dans ce sens que j'ai considéré qu'au niveau de Rs :
La vitesse coordonnées de la lumière est nulle, par contre la vitesse instantannée est égale à c.

La vitesse de la lumière coordonnée est la projection de la vitesse instantannée de la lumière (toujours égale à c pour une raison que j'ignore) en un point dans le système de coordonnées de l'observateur.
Les deux vitesses ne sont égales que si les positions de l'observateur et du point considéré coincident.

Cordialement,
Zefram

un autre de tes schémas en PJ

[Mailou75]

La vitesse coordonnées de la lumière est nulle, par contre la vitesse instantanée est égale à c.
La vitesse de la lumière coordonnée est la projection de la vitesse instantanée de la lumière (toujours égale à c pour une raison que j'ignore) en un point dans le système de coordonnées de l'observateur.
Les deux vitesses ne sont égales que si les positions de l'observateur et du point considéré coincident.

C'est du Zefram ou bien ?

un autre de tes schémas en PJ

Du lourd celui là
En l’occurrence le pointillé noté "c" est la vitesse lumière, quel que soit l'observateur elle n'est jamais nulle et reste constante, toujours la même droite !
On voit que la droite c est tangente à la trajectoire vue par l'observateur à 3,4km (bleu foncé) à l'altitude où, sur le graph de droite, la vitesse vaut c (=1).
Au delà je ne sais pas ce que ça voudrait dire d'ailleurs, j'ai considéré cet observateur comme un cas limite...

[Zefram Cochrane]

Bonjour,
Pour ta question c'est du ou bien.
Dans ce graph de Mailou,

Il y a quatre couples de courbes partant de différentes altitudes x.(2 RS, 4 Rs, 7 Rs et l'oo)
les courbes de gauche se rejoignent Rs avec une vitesse nulle; celles de droite touchent avec une vitesse inférieure ou égale à c selon leur altitude de départ.

Celle de gauche correspondent à la vitesse coordonnée de la capsule en chute libre c'est à dire la projection de la vitesse sur le système de coordonnées (SC) de l'observateur à l'oo. C'est à dire

Celle de droite correspond à la vitesse locale

Si la vitesse coordonnée est nulle au niveau de Rs c'est parce que la vitesse de la lumière coordonnées est nulle, la relation entre la vitesse coordonnée et la vitesse locale est
pour une trajectoire de genre lumière :



où :
est la vitesse instantannée de la lumière
est la vitesse coordonnée de la lumière.

Connaissant la masse du Soleil M, la constante de gravtation G, la vitesse instantannée de la lumière c
donne un rayon Rs d'environ 3km.

Ceci posé ce Rs est normalement un invariant relativiste puisque composé de deux constantes et de la masse un invariant relativiste.

Mais si cela est le cas cela veut dire que
n'est pas égal à
puisque :
r' est la distance de l'observateur stationnaire du centre du TN dans son propre SC exemple la Terre est à 150 000 000 de km
r est la distannce de la distance de l'observateur stationnaire du centre du TN dans le SC de l'observateur à l'oo.
Donc r' > r

Si je suis à l'oo, de mon point de vue la vitesse de la lumière au niveau de l'orbite héliocentrique de la Terre est < c (vitesse coordonnée) .

SI je suis au niveau de l'orbite héliocentrique de la Terre. Comme puis-je calculer ( sans faire d'approximation) la vitesse de la lumière coordonnées au niveau de l'observateur à l'oo?

Cordialement,
Zefram

[Amanuensis]

Celle de droite correspond à la vitesse locale

Pas de sens physique.

[Amanuensis]

SI je suis au niveau de l'orbite héliocentrique de la Terre. Comme puis-je calculer ( sans faire d'approximation) la vitesse de la lumière coordonnées au niveau de l'observateur à l'oo?

Vitesse-coordonnées selon quel système de coordonnées?

(Toutes les questions, et tout le fil, achoppe sur ce "détail" dès qu'on parle de vitesse...)

[Zefram Cochrane]

Bonjour,
Je vais reformuler la question


Si je suis à l'oo; dans mon SC , la vitesse coordonnée de la lumière au niveau de l'orbite héliocentrique de la Terre ( r dans mon SC) est < c (vitesse coordonnée) .

Si je suis au niveau de l'orbite héliocentrique de la Terre (r' = 150 000 000 km dans mon SC) . Comment puis-je calculer dans mon SC ( sans faire d'approximation) la vitesse coordonnée de la lumière au niveau de l'observateur à l'oo?

Cordialement,
Zefram

[Amanuensis]

Si je suis au niveau de l'orbite héliocentrique de la Terre (r' = 150 000 000 km dans mon SC) . Comment puis-je calculer dans mon SC

Commencer par définir ce qu'est le système de coordonnées si laconiquement décrit comme "mon SC".

[Amanuensis]

Je vais donner un exemple simple.

Le tenseur métrique à distance ρ dans le SC de Schw., limité à deux coordonnées, est diag(1-R/ρ, -(1-R/ρ)^-1).

Si on prend comme système de coordonnées alternatif t' =\sqrt(1-R/ρ) t , et r' = r/\sqrt(1-R/ρ), le tenseur métrique local devient diag(1, -1), et la vitesse-coordonnée locale de la lumière dans le sens radial devient 1.

La vitesse coordonnée radiale de la lumière à l'infini devient, dans ce SC là, dr'/dt' = dr/dt 1/(1-R/ρ) = 1/(1-R/ρ).

Mais est-ce que ce SC est "mon SC" ?????

[Mailou75]

Re vous,

Si la vitesse coordonnée est nulle au niveau de Rs c'est parce que la vitesse de la lumière coordonnées est nulle, la relation entre la vitesse coordonnée et la vitesse locale est
pour une trajectoire de genre lumière :

T'es sur que t'as le droit d'écrire ça... ds²=0 parce que c'est la lumière en Schw ?

est la vitesse instantannée de la lumière
est la vitesse coordonnée de la lumière.

... dans ce cas ces égalités sont vraies.
Mais je ne suis pas très chaud sur les termes des vitesses "instantanée" et coordonnée "de la lumière", t'as des sources qui l'énoncent comme ça ?

Mais si cela est le cas cela veut dire que
n'est pas égal à

Oui, ça on le sait déjà

Comme puis-je calculer ( sans faire d'approximation) la vitesse de la lumière coordonnées au niveau de l'observateur à l'oo?

De la façon dont tu l'as fait puisque tu en donnes toi même la définition

.........

Celle de droite correspond à la vitesse locale

Pas de sens physique.

Ah? j'ai pourtant donné la même réponse... c'est la vitesse relative instantanée (dans le repère en mouvement) de l'environnement fixe par rapport au repère en mouvement !
Et je commence à me demander si, dans le premier graph linké par Zef, ce ne sont pas tous les observateurs fixes qui "ont raison", l'objet en chute libre ralentis peu avant 2Rs pour arriver en Rs avec une vitesse nulle. Ca veut dire que l'observateur en chute libre est le seul à penser qu'il continue d'accélérer, simplement parce qu'il compte une peu moins de temps pour parcourir des distances un peu plus grandes car il se rapproche de la masse.
Et de fil en aiguille... un objet ayant une orbite elliptique prononcée accélère-t-il réellement au périastre ou conserve-t-il une vitesse constante (aucune accélération subie) sur sa "géodésique" ?

Vitesse-coordonnées selon quel système de coordonnées?
(Toutes les questions, et tout le fil, achoppe sur ce "détail" dès qu'on parle de vitesse...)

Celui du "repère en mouvement" (voir plus haut) ?

Je vais donner un exemple simple.

Simple ? Et celui des geodésiques ?
C'est sympa de répondre mais faudrait essayer d'être un poil pédagogue, nous faire savoir que tu sais ne suffit pas... seul quelqu'un qui connait déjà la réponse peut comprendre tes réponses.
Tu peux transmettre le savoir sans le perdre, ça pourrait donner des fils intéressants

A+
Mailou

[Zefram Cochrane]

un petit coup d'oeil



Par contre j'ai une question :
correspond à une distance mais laquelle? Dans quel SC? si la question a un sens.


Cordialement,
Zefram

[Amanuensis]

Par contre j'ai une question :
correspond à une distance mais laquelle? Dans quel SC? si la question a un sens.

Dans l'exemple que j'ai pris c'est la coordonnée du point de référence, coordonnée dans le SC de Schw., soit celui "à l'infini".

[Mailou75]

[@Amanuensis] C'est sympa de répondre mais faudrait essayer d'être un poil pédagogue

C'est vrai que mon niveau en maths n'aide pas... (surtout sur les geodésiques)

Dites, vous vous éloignez du sujet initial... j’espère que c'est pour mieux y revenir

(Rappel : si, pour des photons partis radialement de Rs à c, un observateur à l'infini les reçoit avec un redshift infini (temps figé), à quel redhift les reçoit un observateur qui n'est pas à l'infini ?)

[Zefram Cochrane]

Carrément lié
Zef'

[Zefram Cochrane]

Bonjour,
Je reviendrai la vitesse propre plus tard ainsi que sur l'exemple (simple ) d'Amanuensis.

On part de la métrique de Schwarzschild qui pour une trajectoire radiale donne :
(1)

En reprenant la notation d'Amanuensis.
La vitesse coordonnée (lumière ou autre) est la projection de la vitesse propre (ou instantannée ) sur un Système de coordonnées (SC)

la vitesse propre est la variation de la distance propre sur une durée propre je vous propose la notation suivante
Vo est la vitesse propre.
S'il sagit de la vitesse de la lumière

dans l'équation des champs ci dessus


Pour une trajectoire de genre lumière
->

Est ce que cela suffit pour démontrer que localement, ?

On a en outre

pour une trajectoire de genre lumière.


est la vitesse coordonnée de la lumière. Cette vitesse devient nulle pour


Reprenons l'équation (1) pour uen trajectoire de genre lumière



Si je dit que dt' est la période d'une onde lumineuse et dr' sa longueur d'ondre


Je divise pas et je pose
j'ai


Du point de vue ondulatoire, la RG (sous entendu dans le cadre de la métrique de Schwarzschild ) dit qu'une onde lumineuse est infiniment redschifté à Rs du point de vue de tout observateur externe au TN.

Du point de vue corpusculaire, la vitesse coordonnée d'un photon est nulle en Rs parce qu'il ne sera perçu par tout observateur externe au TN que dans un temps infini parce qu'il doit parcourir une distance infinie pour s'échapper de l'horizon du TN. Il lui est impossible de gagner les abords immédiats extérieurs de l'horizon du TN.

Je pense que les deux point de vus sont équivalent bien qu'il faille faire fi de la logique qui doit trouver étrange de parler d'une longueur d'onde infinie (point de vue ondulatoire) pour un photon dont on ne verra jamais la couleur (point de vue corpusculaire).

Cela étant puisque

et si j'ai bien compris


et


La vitesse coordonnée d'un photon au niveau de l'horizon du TN est nulle dans le SC local à du TN ( pour l'observateur dans ce SC) pour l'observateur à l'oo.

Puis-je déduire que avec Rs' différent de Rs ?

Cordialement,
Zefram

[invite60be3959]

Bonjour a tous,

Quelque chose me dérange dans la valeur que l'on fixe pour l'horizon des évènements d'un trou noir de Schwarzschild, le fameux Rs.
Je ne comprends pas pourquoi cette valeur est conservée pour tout observateur alors qu'elle devrait justement dépendre de la position de celui ci.
J'avais déjà abordé le sujet mais je vais essayer de décrire plus amplement ce que je comprend et j'aimerais beaucoup avoir vos critiques sur l'erreur dans le raisonnement...

Salut,

l'erreur réside principalement dans l'interprétation que tu fais de la coordonnée r(en coordonnées de Schwarschild). Dans un espace-temps courbe, elle n'a à peu près rien à voir avec la coordonnée radiale cartésienne à laquelle on a l'habitude. C'est en fait juste un paramètre qui sert à décrire l'évolution des composantes de la métrique. Son lien avec la distance(le long d'une géodésique) est non-trivial. Par exemple la distance entre 2 points très proches de coordonnées et est donnée par :



Le premier terme est un terme cartésien, le second montrant la courbure de l'espace.

Ce "r" n'a donc pas à être affublé d'un rôle qui n'est pas le sien. Le rayon de Schwarschild est la valeur du paramètre "r" qui sépare 2 régions de l'espace-temps bien distinctes, quelque soit la position d'un observateur, mais ce n'est pas le rayon (au sens cartésien) de l'horizon d'un trou noir. Par abus de language on ne fait pas la différence.

[Zefram Cochrane]

Bonjour Vaincent,
Je pense que ton interprétation du paramètre r est erronnée.
L'univers de Schwarzschild est un univers infini avec au centre une sphère de masse M et de rayon Ro.

Ton calcul donne ( approximativement ) la distance réelle à parcourir pour aller de R1 à R2 du point de vue de l'observateur à l'oo.

http://forums.futura-sciences.com/as...ml#post3757951

http://forums.futura-sciences.com/as...ml#post3759432

soit deux observateurs stationnaires: situé à la surface d'une planète de masse M et sur une plateforme perchée à une certaine hauteur de .

Pour l'observateur à l'oo :
est situé à l'altitude
est situé à l'altitude
La longueur de la perche est

Mais connaissant la métrique de Schwarzschild il sait qu'en réalité la longueur de la perche qui est en apparence de longueur


Pour l'observateur stationnaire
est situé à l'altitude
est situé à l'altitude
La longueur de la perche est

la longueur réelle de son point de vue qu'il devra parcourir pour rejoindre
est défini par .


comme

on en déduit que


Pour l'observateur stationnaire
est situé à l'altitude
est situé à l'altitude
La longueur de la perche est

la longueur réelle de son point de vue qu'il devra parcourir pour rejoindre
est défini par .


comme

on en déduit que


La dernière partie de ton message est ambigu
Cordialement,
Zefram

[invite60be3959]

Ce que je dis est basé sur des livres de relativité générale comme Gravitation Relativiste de Rémi Hakim ou encore ce cours de master 2 enseigné à l'université Paris-Diderot (Paris VII). Dans ces références, tu y trouveras que la coordonnée r de Schwarzschild n'a pas de sens physique en tant que distance, mais est simplement une coordonnée sur la variété espace-temps. Les qq formules que tu exposes sont basées sur une compréhension à la relativité restreinte de la métrique de Schwarzschild, en utilisant les composantes de la métrique comme des facteurs de Lorentz, qui montre une vision "plate" d'un espace-temps courbe(d'où la mécompréhension qu'est la tienne ainsi que celle de Mailou75). En relativité générale on ne parle pas d'observateur ici ou là, on parle de systèmes de coordonnées. Ce n'est pas du tout le même language qu'en relativité restreinte, justement parce que la variété espace-temps représente un espace-temps courbe d'un point de vue euclidien ou minkowskien. Par exemple on dira qu'en coordonnées de Schwarzschild, il existe une singularité(de coordonnée) en r=Rs, alors qu'en coordonnées d'Eddington-Finkelstein, cette singularité n'existe pas. Mais, toujours dans ce système de coordonnées, on montre que les géodésiques radiales "sortantes" pour r<Rs, se comportent comme des géodésiques radiales entrantes(la composante radiale de la vitesse coordonnée d'un photon est négative), ce qui montre qu'un photon émis en r<Rs ne peu atteindre un point de la région r>Rs et donc que ces 2 régions ne sont pas liées causalement.

Ce qu'il faut retenir de tout cela, c'est qu'il n'existe pas plusieurs Rs selon l'observateur. Par contre quelque soit le système de coordonnées utilisé, on constate qu'un photon émis en r<Rs ne peut atteindre une région dans la laquelle r>Rs et donc que cette valeur de r=Rs sépare l'espace-temps de Schwarzschild en 2 régions distinctes non-liées causalement.

[invitea29d1598]

salut

Dans ces références, tu y trouveras que la coordonnée r de Schwarzschild n'a pas de sens physique en tant que distance, mais est simplement une coordonnée sur la variété espace-temps.

on peut cependant la relier à une distance physique : une valeur donnée de la coordonnée radiale de Schwarzschild correspond au quotient entre la circonférence équatoriale de la sphère passant par tous les points et 2 pi, soit .

[Amanuensis]

Par contre quelque soit le système de coordonnées utilisé, on constate qu'un photon émis en r<Rs ne peut atteindre une région dans la laquelle r>Rs et donc que cette valeur de r=Rs sépare l'espace-temps de Schwarzschild en 2 régions distinctes non-liées causalement.

L'analyse dans d'autres systèmes de coordonnées montre que les régions sont liées causalement au même sens que normal: le passé influence le futur mais pas réciproquement. La zone I (celle r>R et t quelconque en coordonnées de Schw.) influence causalement le futur, donc en particulier la zone II (l'intérieur du trou noir) qui est "située" dans son futur. Et réciproquement la zone II n'influence pas son passé (dont la zone I). Rien de vraiment particulier...

[invite60be3959]

salut



on peut cependant la relier à une distance physique : une valeur donnée de la coordonnée radiale de Schwarzschild correspond au quotient entre la circonférence équatoriale de la sphère passant par tous les points et 2 pi, soit .

Effectivement, mais j'ai préféré éviter d'en parler dans un premier temps de peur de semer la confusion avec la coordonnée radiale euclidienne.

[Amanuensis]

C'est plutôt de parler de "coordonnée radiale euclidienne" qu'on peut taxer de confusion. Les coordonnées de Schwarzschild n'ont pas à être vues comme euclidiennes.

[invite60be3959]

L'analyse dans d'autres systèmes de coordonnées montre que les régions sont liées causalement au même sens que normal: le passé influence le futur mais pas réciproquement. La zone I (celle r>R et t quelconque en coordonnées de Schw.) influence causalement le futur, donc en particulier la zone II (l'intérieur du trou noir) qui est "située" dans son futur. Et réciproquement la zone II n'influence pas son passé (dont la zone I). Rien de vraiment particulier...

Bien évidemment, ces 2 régions sont liées causalement dans le sens I->II. Je parlais du lien causal II->I qui n'existe pas, et qui fait qu'un trou noir est noir. ça c'est particulier.