Solubilité ideale

[mau13]

Bonsoir à tous,

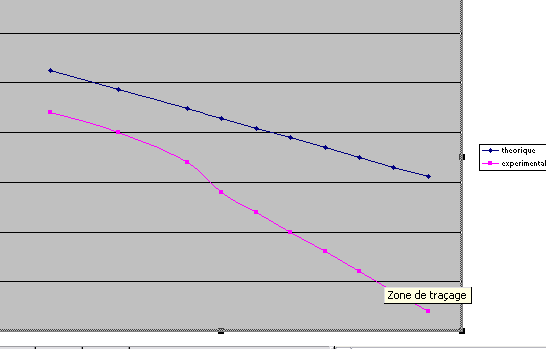
Voici une courbe représente logX =f(1/T) avec X fraction du composé a T de solubilité(solide se dissolve)
En bleu (droite) logX =f(1/T) c’est la courbe théorique pour une solution idéal.
En violet c’est la courbe expérimentale.
Le système étudié est le binaire Hexane-Heptane. Comme ces composés ont une constitution chimique voisine,on devrait avoir une solubilité qui converge vers l’idéal.

Vous remarquerez que les deux courbes sont parallèles dans un premier temps, puis à une certaine température l’on constate la divergence de la courbe expérimentale.

Comme expliqué déjà le premier écart entre la courbe expérimental et théorique.
Et a quoi est du la divergence subite de la courbe expérimental (à une certaine température).
Merci.

Ps :si vous avez des documents concernant la solubilité idéal,ils seraient bienvenu.
-----

[invite3fe28b67]

bsr a toi.puisque la température influence la cst de solubilité Ks qui est une cst thrmodynamique je pense que yout se joue autour .et puisque la solution est idéales il faut que vous voyez le cour des sol idéal et réelbn courage

[mach3]

la pièce n'est pas encore validée. Je n'ai pas de doc sous la main par contre je peux exposer le concept.

Prenons deux constituants A et B à l'état liquide (par exemple, mais on peut aussi parler de solution solide idéale). Si on prend A pur, il n'y a que des interactions A-A qui vont contribuer à l'enthalpie, de même si on prend B pur, il n'y a que des interactions B-B.
Effectuons un mélange, certaines interactions A-A et B-B vont être brisées au profit d'interactions A-B, il y aura donc logiquement une variation d'enthalpie suite à cette destruction/création de liaison.
On considère que la solution est idéale lorsque cette enthalpie est nulle (ou peut être considérée comme nulle), les liaisons A-B crées compensent exactement les liaisons A-A et B-B détruites.

Cela ce décline autrement quand on passe à l'enthalpie libre. On peut démontrer qu'en prenant un état de référence correspondant au constituant pur, l'activité a est égale à la fraction molaire dans la formule suivante :

, ou µ° est le potentiel chimique de l'état de référence, donc du constituant pur.

Etant donné une solution idéale, son équilibre avec un solide est décrit par la formule de Schroeder-Van laar si c'est un constituant, Prigogine-Defay si c'est un composé défini (ces deux formules se démontrant assez simplement).

Dans le cas d'un constituant, on prend donc Schroeder-Van laar. Si on fait l'hypothèse (gonflée) que l'enthalpie de fusion ne dépend pas de la température, alors logX =f(1/T) est linéaire.
Un écart à cette linéarité à deux sources :
-d'abord la variation de l'enthalpie de fusion
-ensuite l'écart à l'idéalité (la non nullité de l'enthalpie de mélange du liquide)

m@ch3

[invite3fe28b67]

la pièce n'est pas encore validée. Je n'ai pas de doc sous la main par contre je peux exposer le concept.

Prenons deux constituants A et B à l'état liquide (par exemple, mais on peut aussi parler de solution solide idéale). Si on prend A pur, il n'y a que des interactions A-A qui vont contribuer à l'enthalpie, de même si on prend B pur, il n'y a que des interactions B-B.
Effectuons un mélange, certaines interactions A-A et B-B vont être brisées au profit d'interactions A-B, il y aura donc logiquement une variation d'enthalpie suite à cette destruction/création de liaison.
On considère que la solution est idéale lorsque cette enthalpie est nulle (ou peut être considérée comme nulle), les liaisons A-B crées compensent exactement les liaisons A-A et B-B détruites.

Cela ce décline autrement quand on passe à l'enthalpie libre. On peut démontrer qu'en prenant un état de référence correspondant au constituant pur, l'activité a est égale à la fraction molaire dans la formule suivante :

, ou µ° est le potentiel chimique de l'état de référence, donc du constituant pur.

Etant donné une solution idéale, son équilibre avec un solide est décrit par la formule de Schroeder-Van laar si c'est un constituant, Prigogine-Defay si c'est un composé défini (ces deux formules se démontrant assez simplement).

Dans le cas d'un constituant, on prend donc Schroeder-Van laar. Si on fait l'hypothèse (gonflée) que l'enthalpie de fusion ne dépend pas de la température, alors logX =f(1/T) est linéaire.
Un écart à cette linéarité à deux sources :
-d'abord la variation de l'enthalpie de fusion
-ensuite l'écart à l'idéalité (la non nullité de l'enthalpie de mélange du liquide)

m@ch3

j'ai crue je la thermo était mon point fort .aprés que j'ai lu ta rép bah moi non lpus j'ai rien piger a propos des corps purs

[A voir en vidéo sur Futura]

[mau13]

la pièce n'est pas encore validée. Je n'ai pas de doc sous la main par contre je peux exposer le concept.

Prenons deux constituants A et B à l'état liquide (par exemple, mais on peut aussi parler de solution solide idéale). Si on prend A pur, il n'y a que des interactions A-A qui vont contribuer à l'enthalpie, de même si on prend B pur, il n'y a que des interactions B-B.
Effectuons un mélange, certaines interactions A-A et B-B vont être brisées au profit d'interactions A-B, il y aura donc logiquement une variation d'enthalpie suite à cette destruction/création de liaison.
On considère que la solution est idéale lorsque cette enthalpie est nulle (ou peut être considérée comme nulle), les liaisons A-B crées compensent exactement les liaisons A-A et B-B détruites.

Cela ce décline autrement quand on passe à l'enthalpie libre. On peut démontrer qu'en prenant un état de référence correspondant au constituant pur, l'activité a est égale à la fraction molaire dans la formule suivante :

, ou µ° est le potentiel chimique de l'état de référence, donc du constituant pur.

Etant donné une solution idéale, son équilibre avec un solide est décrit par la formule de Schroeder-Van laar si c'est un constituant, Prigogine-Defay si c'est un composé défini (ces deux formules se démontrant assez simplement).

Dans le cas d'un constituant, on prend donc Schroeder-Van laar. Si on fait l'hypothèse (gonflée) que l'enthalpie de fusion ne dépend pas de la température, alors logX =f(1/T) est linéaire.
Un écart à cette linéarité à deux sources :
-d'abord la variation de l'enthalpie de fusion
-ensuite l'écart à l'idéalité (la non nullité de l'enthalpie de mélange du liquide)

m@ch3

Bonsoir à tous,
Solution idéale :
Serait dire que les deux constituants formant le mélange cohabiterais en phase sans formations de liaisons A-B. (C’est envisageable ? même au meilleur des cas.. !!!)
Ni formations de liaisons A-B ni destruction de A-A équivaut à dire variation d’enthalpie nul, ça serait donc dire que la réaction n’est pas exothermique,y-t-il des cas concrets se tendant vers cette configuration (dégagement de chaleur presque nul?)

Le fichier est valide : on voit que plus T démunie plus l’écart (Théo-experimental) augmente. Le faites que l’enthalpie de fusion dépende de la température expliquerait bien cela.

Le binaire étudié est le heptane-hexane, en termes de caractéristiques que peut on dire de lui en matière d’idéalité.
Le mélange heptane-hexane a tendance à formé des liaisons ?à dégager de la chaleur ?

Ps : quand on parle de solubilité idéale en considère l’idéalité de la solution solide et liquide ?

Merci.

[mach3]

Solution idéale :
Serait dire que les deux constituants formant le mélange cohabiterais en phase sans formations de liaisons A-B. (C’est envisageable ? même au meilleur des cas.. !!!)
Ni formations de liaisons A-B ni destruction de A-A équivaut à dire variation d’enthalpie nul, ça serait donc dire que la réaction n’est pas exothermique,y-t-il des cas concrets se tendant vers cette configuration (dégagement de chaleur presque nul?)

ce que tu décris ici, c'est quand A et B sont non miscibles. Si ils sont miscibles, alors il y a forcément des molécules A et des molécules B au voisinage d'une molécule donnée, donc forcément des interactions A-B.

Le binaire étudié est le heptane-hexane, en termes de caractéristiques que peut on dire de lui en matière d’idéalité.

les deux se ressemblent vraiment beaucoup, mais ils n'ont pas la même parité en nombre de carbone. Expérimentalement il a été mis en évidence que les chaines carbonées ont tendances à se grouper par parité (on a par exemple des solutions solides C6-C8 ou C8-C10 mais pas C6-C7) en phase solide, je ne sais pas ce qu'il en est en phase liquide, c'est surement beaucoup moins gênant.
Quoiqu'il en soit, à faible fraction molaire, le mélange devrait être idéal. Il l'est peut-être plus loin d'ailleurs et dans ce cas la seule source de déviation serait l'enthalpie de fusion qui ne peut être une constante.

est-ce que je pourrais voir la courbe X=f(T) (en normal, sans le log)?

Le mélange heptane-hexane a tendance à formé des liaisons ?à dégager de la chaleur ?

il y a toujours des liaisons de Van der Waals qui vont se former quoi qu'il arrive, et pour ces hydrocarbures je ne vois pas d'autres liaisons possibles. Vu la faiblesse de ces liaisons et la similitude entre les deux constituants, l'enthalpie de mélange doit être vraiment faible.

quand on parle de solubilité idéale en considère l’idéalité de la solution solide et liquide ?

Ca dépend, en général on précise quelle phase est idéale. Dans ton cas la phase liquide est idéale (en théorie) mais pas la phase solide (une phase solide idéale est forcément une solution solide totale et tu cristallises certainement un hydrocarbure pur, pas une solution solide, par ailleurs je ne suis pas sur qu'on la linéarité dans le cas ou liquide et solide sont idéaux, il faut que je vérifie).

m@ch3

[mau13]

Bonsoir,

ce que tu décris ici, c'est quand A et B sont non miscibles. Si ils sont miscibles, alors il y a forcément des molécules A et des molécules B au voisinage d'une molécule donnée, donc forcément des interactions A-B.

C’est juste, je crois comprendre : en faites quand il y a miscibilité, on peut dire que l’idéalité de la solution s’envisage par rapport au degré d’influence des interactions A-B.

Mais justement, quand il y a non miscibilité y a-t- lieu de parler de solution idéale ? !!

les deux se ressemblent vraiment beaucoup, mais ils n'ont pas la même parité en nombre de carbone. Expérimentalement il a été mis en évidence que les chaines carbonées ont tendances à se grouper par parité (on a par exemple des solutions solides C6-C8 ou C8-C10 mais pas C6-C7) en phase solide, je ne sais pas ce qu'il en est en phase liquide, c'est surement beaucoup moins gênant.

Tu dis les chaînes carbonées ont tendance à ce regroupé par parité:
Quand tu dis regroupé (tu fais allusion a la miscibilité en phase solide), je n’ai pas saisi l’impact de cet argument (quand tu dis que ce n’est pas le cas pour C6-C7) ?
(l'impact) Ça serait que la miscibilité d’un binaire d’hydrocarbure en phase solide pourrait s’envisager par rapport à la parité des chaînes carbonées?
En faites je ne t’ai pas vraiment bien saisi quand tu dis que ça doit être moins gênant en en phase liquide.

est-ce que je pourrais voir la courbe X=f(T) (en normal, sans le log)?

Ok,je le rajoute...

Ca dépend, en général on précise quelle phase est idéale. Dans ton cas la phase liquide est idéale (en théorie) mais pas la phase solide (une phase solide idéale est forcément une solution solide totale et tu cristallises certainement un hydrocarbure pur, pas une solution solide, par ailleurs je ne suis pas sur qu'on la linéarité dans le cas ou liquide et solide sont idéaux, il faut que je vérifie).

Trés bien,

Merci.

[mau13]

voila comme demandé m@ch3, X=f(T)
Pièce jointe 47646

[mach3]

Mais justement, quand il y a non miscibilité y a-t- lieu de parler de solution idéale ? !!

non, parce que dans ce cas il n'y a pas de solution!! (le résultat enthalpique du mélange est le même, mais c'est le seul rapport, au niveau entropique c'est totalement différent).

Quand tu dis regroupé (tu fais allusion a la miscibilité en phase solide), je n’ai pas saisi l’impact de cet argument (quand tu dis que ce n’est pas le cas pour C6-C7) ?

expérimentalement on remarque que les chaines de même parité interagissent mieux entre elle en phase solide, ça doit être une question de nombre de zig-zag dans la structure cristalline. En phase liquide il ne devrait pas y avoir de structures qui se gênent quand la parité est différente (vu qu'un liquide n'a que peu de structure local, surtout dans ce cas avec que des liaisons faibles), mais qui sait, à basse température... enfin tout ça pour dire que l'activité peut être influencée, mais c'est de la spéculation.

voila comme demandé m@ch3, X=f(T)

ca marche pas... erreur de manip?

m@ch3

[mau13]

expérimentalement on remarque que les chaines de même parité interagissent mieux entre elle en phase solide, ça doit être une question de nombre de zig-zag dans la structure cristalline. En phase liquide il ne devrait pas y avoir de structures qui se gênent quand la parité est différente

Interagisse mieux : forment des solutions solide tendant vers l’idéalité?.

En disant interagissent mieux, je me pose une question : quand les interactions A-B sont importantes la solution est non idéal,oui.,alors:

Dans la pratique, qu’elles sont les contraintes engendrées par la non idéalité d’un système par rapport à un système dit idéal ? (c.a.d :est-ce plus intéressant de travailler avec un système idéal ?)

[mau13]

ca marche pas... erreur de manip?

Je réitère :

[mau13]

Je réitère :
Pièce jointe 47715

Cela ne correspond pas à ce que tu presentais?

[mach3]

re

désolé j'avais zappé

vu la forme de la courbe il peut y avoir une autre cause à cet écart à l'idéalité : un composé défini non congruent ou un polymorphe (voire les deux ou plusieurs?)

Ta courbe de solubilité présente des inflexions, ce qui est caractéristique de la présence d'invariants (peritectiques, transition polymorphique).

Après c'est qu'une hypothèse, les points de la courbes sont expérimentaux et je ne connais pas la marge d'incertitude.

m@ch3

[mau13]

désolé j'avais zappé

no problemo

vu la forme de la courbe il peut y avoir une autre cause à cet écart à l'idéalité : un composé défini non congruent ou un polymorphe (voire les deux ou plusieurs?)

Tu m'en avais déja parler,definie comme etant un solide qui rend du jus,mais cela voudrait dire au juste que la cristalisation observé( courbe) n'est pas celle du corps pur mais plutot du Péritectique?

[mach3]

mais cela voudrait dire au juste que la cristalisation observé( courbe) n'est pas celle du corps pur mais plutot du Péritectique?

c'est à peu près ça (si l'hypothèse est correcte). Le début de la courbe (hte température) est bien la solubilité du composé pur, mais en descendant, il se peut qu'à partir de la premiere inflexion ça ne soit plus le composé pur, mais un composé défini (qui fini en peritectique aux environs du point d'inflexion).

Mais ça peut être aussi un polymorphe, c'est à dire que la courbe de solubilité est toujours celle du produit pur, mais pas du même solide.

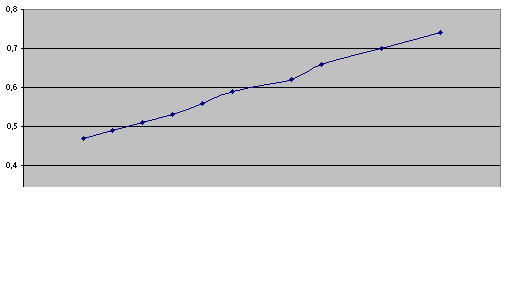
Tout cela évidemment sous réserve que l'incertitude de ta courbe ne soient pas trop élevée, sinon on peut disserter des heures sur des milliers d'hypothèses imaginables sans que ça ait le moindre intérêt pratique (ça reste intéressant, mais ça ne résout pas le problème)

m@ch3