Calcul de la déviation lumineuse au voisinage du soleil par Newton

[increa]

Bonjour,depuis quelques jours j'ai essayé de comprendre comment calculer la déviation d'un rayon lumineux passant au voisinage du soleil.
En effet une intervention de "Lansberg" dans son message 1556 du sujet "mesure de la vitesse de la lumière selon Romer" m'a interpellé.
celui ci disait:
@Lansberg
"Si on tient compte de l'intégralité de l'hyperbole décrite par un rayon lumineux passant à proximité d'un corp massif,la théorie de Newton donne le même résultat que la RG."

Cette phrase a soulevé un doute en moi car j'avais toujours entendu dire que la déviation de l'angle prévue par Einstein était le double de la déviation de l'angle prévue par la théorie de Newton.
Aussi, je me suis mis en marche pour enquêter sur cette affirmation.
Début de la justification du calcul.

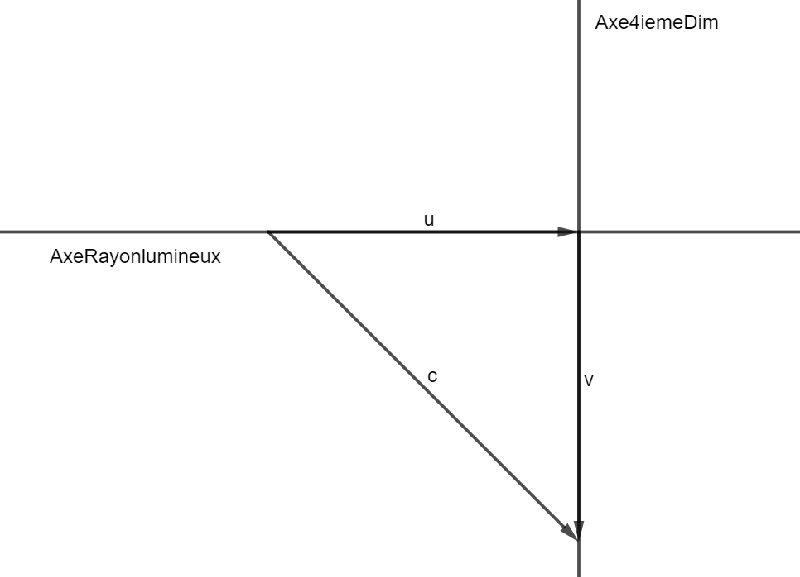
Dans un repère où un rayon de lumière passe par un point tangent O du soleil, je choisi comme axe des x la direction de fuite du rayon, et comme axe y l'axe qui passe par le centre du soleil (c) et le point O.(voir figure ci dessous)
Soleil.jpg
Dans ce repère donc, la déviation du rayon lumineux est au départ:
1/
d'où en dérivant


où gmoy est la valeur moyenne de la composante verticale de la gravité entre le point O sur le soleil calculée tout le long de son déplacement L.
où Ms est la masse du soleil, Rs est le demi-diamètre du soleil et G la constante fondamentale de la Gravitation.
d'autre part, on considère que l'intervention de la gravitation sur la vitesse de la lumière est minime puisque la vitesse de libération au niveau du point O est de quelques centaines de km/s à comparer à 300 000 km/s.

calcul de la composante moyenne perpendiculaire au déplacement de l'attraction du soleil sur une longueur L:
2/

Pour simplifier on pose
de l'équation 2 on déduit:
3/

qui devient dès que 1 est négligeable devant k²

4/

de 1,3 et 4 j'en déduis que la demie déviation

Donc comme l'explique la figure ci dessous
Soleil 2.jpg

Ainsi nous voyons que contrairement aux affirmations de Lansberg la déviation prévue par Newton est deux fois moindre que celle prévue par Einstein et ce en prenant en compte la totalité de l'hyperbole.
Une des conclusions ,si l'on suppose que la taille et la masse du soleil sont des constantes, est que vis à vis de la mécanique Newtoniène la constante G pour les phénomènes lumineux est le double de ce quelle est pour les autres objets.
D'où ma reflexion un rayon de lumière tombe deux fois plus vite qu'une pomme symbolisée par l'expression y=gt^2 qui semblait aussi choquer @mach3.
-----

[invitedd63ac7a]

Cette phrase a soulevé un doute en moi car j'avais toujours entendu dire que la déviation de l'angle prévue par Einstein était le double de la déviation de l'angle prévue par la théorie de Newton.

Je ne savais pas que la mécanique Newtonienne prévoyait la déviation des rayons lumineux par une masse. Il me semblait que c'était Einstein et sa relativité général qui prévoyait ce phénomène.

[Gilgamesh]

Je ne savais pas que la mécanique Newtonienne prévoyait la déviation des rayons lumineux par une masse. Il me semblait que c'était Einstein et sa relativité général qui prévoyait ce phénomène.

Pour Newton, la lumière a une nature particulaire (formée de particule de masse inconnue mais très petite), donc elle tombe dans le champs de gravité comme n'importe quel corps.

[increa]

Une autre explication possible serait que la vitesse de la lumière en provenance des étoiles serait :

Mais ça, c'est contraire à la charte du forum

[A voir en vidéo sur Futura]

[JPL]

C’est surtout une connerie scientifique.

[invitedd63ac7a]

Rassurez-moi, ils y auraient des physiciens qui avant Einstein auraient calculé une déviation de la lumière au voisinage des astres avec la mécanique newtonienne ?
Il y a bien les hypothèses de John Michell en 1783 et de PS de Laplace en 1796 mais je ne pense pas qu'elles aient été accompagnées de quelques calculs. Non ?

[Lansberg]

Bonjour,

Rassurez-moi, ils y auraient des physiciens qui avant Einstein auraient calculé une déviation de la lumière au voisinage des astres avec la mécanique newtonienne ?

Oui ! En particulier Soldner en 1801 que je citais dans la discussion précédente évoquée par increa. Ce dernier a bien calculé la déviation d'un rayon lumineux passant à proximité d'un astre. Pour le Soleil il trouve un angle de 0,84". Comme il le précise, cet angle ne tient compte que d'une 'moitié' d'hyperbole. Il faudrait donc multiplier par 2 ce qui donnerait pratiquement la valeur calculée par Einstein.
Après relecture de l'article et les remarques de mach3, on découvre effectivement une erreur commise par Soldner. L'angle de 0,84" concerne bien la déviation totale.
Toujours est-il que la mécanique newtonienne permet de prévoir une déviation. Einstein, un siècle plus tard, mènera, dans un premier temps, le même raisonnement.

[Deedee81]

Salut,

Une autre explication possible serait que la vitesse de la lumière en provenance des étoiles serait :

L'aberration stellaire montre que la lumière qui vient des étoiles va à la vitesse c.
(et la mesure de Römer, bien améliorée depuis, montre qu'elle va aussi à c dans le système solaire)

Mais ça, c'est contraire à la charte du forum

L'affirmer, oui, puisque ce serait faux.
Mais c'est surtout une bêtise du fait que tu n'as pas pris la peine d'étudier le sujet.

Concernant la question initiale.

Dans ce livre :
#######
Le livre est Relativité Générale de Edgard Elbaz

Tu as le détail de ce calcul. Fait de manière très simple d'ailleurs (beaucoup plus que ce que tu as donné ci-dessus).

[invitedd63ac7a]

Oui ! En particulier Soldner en 1801 que je citais dans la discussion précédente évoquée par increa. Ce dernier a bien calculé la déviation d'un rayon lumineux passant à proximité d'un astre

Là, j'ai appris quelque chose, merci. Je ne pensais pas qu'un tel calcul avait pu être mené avant ceux d'Einstein.

[increa]

Question ouverte:

soit le schéma ci dessus où:

Quelle mesure de la vitesse u ferait un expérimentateur qui se déplace dans l'espace temps à la vitesse v?
Son temps propre dilaté d'un facteur
combiné à la vitesse u donnerait la distance:

Il trouverait donc que la vitesse u est égale à celle de la lumière...quelque soit la direction choisie...

[increa]

Salut,


Dans ce livre :
#######
Le livre est Relativité Générale de Edgard Elbaz

Bonjour, l'adresse me demande mon n° de carte bleue est ce normal?

[Deedee81]

Bonjour, l'adresse me demande mon n° de carte bleue est ce normal?

Bonjour,

Non, ce n'est pas normal. En outre je viens de voir (ou plutôt d'être informé par MP) que ce site était louche (un site comme celui-là en Colombie !!!).
Cela m'avait échappé et j'en suis sincèrement désolé.

Donc je m'auto-modère. Et j'ai donné ci-dessus la référence du livre en question au cas où cela vous intéresserait.
Attention, pour apprendre la relativité générale il est je trouve pas idéal (trop axé sur l'approche calculs avec les composantes). Ceci dit, c'est aussi une question d'appréciation.
En outre ce livre contient pleins de calculs fort pratiques (comme celui sus-nommé mais aussi les coefficients des métriques dans toute une série de cas, c'est parfois bien pratique).

[Resartus]

Bonjour,
Au vu des échanges, je me demande s'il n'y aurait pas confusion dans les souvenirs de certains intervenants entre la déviation de la lumière au voisinage d'une masse, et l'autre phénomène qui est lui est purement RG : un léger excès* d'avance du périhélie de Mercure

*sachant que la plus grosse partie de l'avance s'explique sans RG par l'influence des autres planètes. Sur les 5600 secondes par siècle d'avance mesurés, seulement 43 étaient inexpliqués

[Deedee81]

SAlut,

Au vu des échanges, je me demande s'il n'y aurait pas confusion dans les souvenirs de certains intervenants entre la déviation de la lumière au voisinage d'une masse, et l'autre phénomène qui est lui est purement RG : un léger excès* d'avance du périhélie de Mercure
*sachant que la plus grosse partie de l'avance s'explique sans RG par l'influence des autres planètes. Sur les 5600 secondes par siècle d'avance mesurés, seulement 43 étaient inexpliqués

Il ne me semble pas avoir vu cette confusion. Qu'est-ce qui tye fait dire ça ?

[increa]

Bonjour,
je revenais sur ce sujet pour préciser mon point de vue dans un texte sur la relativité restreinte un peu plus élaboré qui reprend un dessin et des propos que j'avais énoncé précédemment sur ce fil
##retrait d'une pièce jointe contenant une théorie personnelle, application du point 6 de la charte, mach3 pour la modération##
Cordialement

[Deedee81]

Salut,

Un truc me chiffonne dans ton analyse.
Jusqu'à la formule de chute libre newtonienne, pas de problème (à quelques mini détails près sans importance).
Mais à partir de là, ça ne va pas. Je n'ai pas analysé en détail mais il risque forcément d'y avoir des soucis car :
relativité restreinte et gravité sont incompatibles
(ça se vérifie très facilement, mais je ne retrouve plus le message où j'en parlais)

Donc il y a de fort risques de tomber sur des absurdités.

[azizovsky]

On'a la représentation quadri-vectorielle ! , a=(,c), de pseudo-norme : 2c²-c²=c²:



càd :

[mach3]

Bonjour,
je revenais sur ce sujet pour préciser mon point de vue dans un texte sur la relativité restreinte un peu plus élaboré qui reprend un dessin et des propos que j'avais énoncé précédemment sur ce fil
Pièce jointe 386266
Cordialement

Déjà ça commence mal (mise en gras par moi) :

Relativité restreinte a-t-on bien choisi les bons repères...

Poser une question pareille semble montrer que le fondement même de la relativité (galiléenne, même pas d'Einstein) ne serait pas acquis (en même temps il est généralement tellement mal enseigné et vulgarisé, pas très étonnant et en fait très courant). La relativité c'est justement le fait de pouvoir faire de la physique correctement en travaillant dans n'importe quel repère. Il n'y a pas de bons ou de mauvais repères du point de vue physique, ce ne sont que des outils qui modulent la complexité des calculs. La différence entre relativité galiléenne et einsteinnienne est l'inclusion de l'électromagnétisme, ce qui ne change pas le fond : la physique est indépendante du repère, donc il n'y a pas de bon ou de mauvais repère si ce n'est au niveau de la complexité des calculs.

pourquoi utiliser une pseudo-norme pour faire les calculs vectoriels de la relativité?

le fait que ça donne des résultats conforme aux observations est une raison suffisante.

La réponse trouvée dernièrement implique probablement un certain auto-centrisme de point de vue des personnes qui ont instauré les premiers le formalisme de la relativité restreinte.
Un peu le même auto-centrisme de ceux qui pensaient que le soleil tournait autour de la terre... (Ce qui n'est pas complètement dénué de sens)

Absurde. L'indépendance du repère fait qu'on peut se centrer sur ce qu'on veut, et même travailler sans repère (mais c'est alors souvent bien plus difficile de faire les calculs).

Ainsi dans cette nouvelle théorie crée au début du vingtième sciècle le repère choisi par nos anciens est centré sur notre position spatiale

C'est un repère où les calculs seront simples. Si le résultat n'est pas influencé par le choix du repère, autant choisir un repère où les calculs sont simples.

et dans la quatrième dimension s'écoule le temps à la vitesse de la lumière.

ça ne veut rien dire. Le temps n'est pas un fluide dont on peut mesurer la vitesse (de toutes façons, la vitesse du temps c'est 1 seconde par seconde ).

La conséquence immédiate d'avoir choisi cette vitesse limite de déplacement pour le temps impose par construction l'impossibilité d'y rajouter une vitesse spatiale avec les systèmes de normes habituelles.
En effet, la célérité de la lumière étant donnée à la quatrième dimension il est absolument impossible d'y adjoindre une vitesse spatiale sous peine de voir cette dernière dépassée lorsqu'on calcule la norme du vecteur vitesse quadridimensionnel.

Quelle bouillie... L'espace-temps obéit à la géométrie de Minkowski, c'est tout. Les autres géométries possibles (dégénérée avec un split temps absolu-espace euclidien, et espace-temps euclidien) ne collent pas avec les observations.

C'est impossible, l'expérience de Michelson et Morley [parce que Morlaix c'est en bretagne] est là, bien réelle pour nous en dissuader. La vitesse de la lumière est constante et ne peut être dépassé. D'où la création de cette pseudo-norme qui retranche la partie spatiale à la dimension temporelle.

J'aime pas trop le mot "création". On a surtout choisi parmi les géométries possibles celle qui colle à l'observation.

Enfin, une autre volonté plus subtile s'était caché dans les choix des repères de la relativité restreinte... c'était celle de se débarrasser de l'idée de l'éther luminifère...

non, parce qu'on peut interpréter à la façon de Lorentz. On garde l'espace et le temps absolus, l'éther luminifère y est immobile et agit sur les objets en déplacement par rapport à lui en les raccourcissant et en ralentissant leurs horloges. La vitesse de la lumière est c par rapport à l'éther seulement, mais l'effet de l'éther sur les règles et les horloges en mouvement par rapport à lui fait que toute mesure de la vitesse de la lumière par un observateur en mouvement par rapport à l'éther donne invariablement c : il est du coup impossible de connaitre le mouvement par rapport à l'éther et donc de connaitre le temps absolu (l'espace et le temps absolu, ainsi que l'éther sont du coup non réfutables). Cette interprétation est confortable pour les personnes qui sont mal à l'aise avec la relativité restreinte et comme c'est une interprétation, pas une autre théorie, elle prédit exactement les mêmes résultats que l'interprétation géométrique de Minkowski (les jumeaux de Langevin n'ont pas le même age, on peut fermer les portes de la grange quand l'échelle est dedans, les muons vivent plus longtemps, la ficelle de Bell casse, etc, tout marche). Cela étant dit c'est une ornière pour qui veut aborder la suite, à savoir la relativité générale.

Par ailleurs, il ne s'agit pas d'un choix de repère (vu que le repère on s'en fiche, ce n'est qu'un outil pour moduler la complexité des calculs), mais d'un choix de géométrie...

Je commenterais la suite plus tard, si j'ai le temps...

m@ch3

[azizovsky]

Ceci pour un espace-temps sans courbure, si on courbe ..., on doit 'courber' les relations ci-dessus .

[azizovsky]

le choix de la représentation quadri-vectorielle x(a,b) n'a aucun influence sur 'la réalité' des choses, un moyen sur lequel est projeter une idée ... , par exemple si tu prend C=c/V2 , si on remplace dans la relation du pseudo-norme de la RR (citer en haut) le facteur 1/V2 va disparaître ..., mais le problème où tu'as mesuré une vitesse de la lumière C=c/V2 ? (c :une constante imposer par la nature non pas par les maths ... ).

ps: la pseudo-norme s'en fou complètement de la constante qui s'y injecté ....(une relation mathématique)

[mach3]

un commentaire la-dessus :

Nous savons tous depuis Newton que les objets de notre monde tombent dans un champs gravitationnel en obéissant à la loi:
y= 1/2 g t^2

C'est la formule pour un cas très particulier : la chute d'un corps suivant l'axe y, avec le champ de gravitation suivant l'axe y, une coordonnée y et une vitesse suivant y nulle à l'origine des temps (on parlait justement de choix de repère ) et qui ne va donc s'appliquer correctement sur un grand intervalle de t et y que si g reste aligné sur l'axe y. Donc soit :
-c'est une chute radiale, donc inadapté pour la déviation de quoique ce soit (lumière ou pas) par un corps massif
-c'est une chute dans un champ de gravitation uniforme (par exemple causé par un plan infini) qui n'existe pas dans la réalité et qui est une approximation applicable pour un déplacement orthoradial très faible devant la distance radiale. Rien de remarquable concernant la lumière (ou tout autre corps très rapide) dans ces conditions, le déplacement orthoradial qui permet l'approximation est tellement petit que la "chute" de la lumière n'est même pas mesurable (faudrait faire le calcul sérieusement pour savoir quelle est la différence de prédiction entre mécanique classique et RG sur mettons 100m ou 1km, ça doit pas être bezef de toutes façons).

Bref, ce n'est pas avec cette formule que l'on montrera un désaccord entre la mécanique classique et l'expérience concernant la déviation de la lumière par les masses.

C'est plutôt à la dérivée seconde de la distance radiale qu'il faut s'intéresser. En effet vu depuis la surface du corps attracteur, un corps qui possède une vitesse orthoradiale supérieure à celle qui est nécessaire pour l'orbite circulaire semble tomber "à l'envers" : sa vitesse radiale, plutôt qu'être positive, s'annuler puis devenir négative, est d'abord négative, s'annule puis devient positive. Il y a un terme centripète dû à la gravitation, g, et un terme centrifuge lié à la vitesse orthoradiale. Pour des distances radiales élevées par rapport à GM/c² (M masse du corps attracteur) le terme centripète obtenu en RG est le même qu'en mécanique classique. Pour des vitesses faibles devant c, le terme centrifuge obtenu en RG est le même qu'en mécanique classique. C'est au terme centrifuge qu'il faut s'intéresser pour comprendre la différence de prédiction entre mécanique classique et RG en matière de déviation de la lumière et en fait de tout corps dont la vitesse par rapport au corps attracteur n'est pas négligeable devant c (y compris une pomme qu'on aurait lancée à vive à allure).

m@ch3

[azizovsky]

Pour rayer de la carte le doute :

La seconde, était pourquoi utiliser une pseudo-norme pour faire les calculs vectoriels de la relativité?

, on'a :

simplifier par c²

, on fait la substitution comme https://fr.wikipedia.org/wiki/Relati...%A9_restreinte





c'est une relation mathématique, on peut choisir n'importe quel constante ....mais accepter par la nature .

[mach3]

Je ne vais pas commenter la suite du document qui est une spéculation personnelle gratuite et sans intérêt. Juste quelques points de détails (c'est moi qui ait mis en gras) :

Au total de son périple le jumeau voyageur aura passé 30 ans de sa vie à voyager dans sa fusée et le jumeau paresseux lui aura vécu 5/3 de temps en plus et sera donc âgé de 50 ans alors que son jumeau lui aura vécu 20 ans de moins.
Le paradoxe étant fondé sur la symétrie de point de vue des deux jumeaux qui voient la même chose dans chacun de leurs repères mais qui, au final, constatent une dissymétrie dans leurs âges...

Le passage en gras est faux. Justement, ils ne voient pas la même chose. Dans le cas décrit, le sédentaire voit le voyageur ralenti d'un facteur 3 pendant 45 ans (en 45 ans il voit le voyageur en prendre 15), puis il voit le voyageur à vitesse accélérée d'un facteur 3 pendant 5 ans (en 5 ans il voit le voyageur prendre 15 ans), alors que le voyageur voit le sédentaire ralenti d'un facteur 3 pendant 15 ans (en 15 ans il en prend 5) et accéléré d'un facteur 3 pendant 15 ans (en 15 ans il en prend 45).
Il n'y a pas du tout symétrie des points de vues.

Les résultats sont identiques à ceux donné par la relativité restreinte mais cette fois ci, il ne peut y avoir de confusion entre les deux jumeaux qui ont vécu deux parcours différents

il ne peut pas y avoir de confusion non plus en relativité restreinte...

on trouve des résultats identiques à ceux de la relativité restreinte, mais le paradoxe de Langevin a disparu.

En relativité restreinte l'expérience des jumeaux de Langevin n'est pas un paradoxe, il n'y a donc pas lieu de le faire disparaitre...

Je vous suggère la lecture de cet ancien post assez complet (pas si vieux que ça) : https://forums.futura-sciences.com/p...ml#post6336638

La vitesse et les durées diffèrent mais c'est qualitativement la même chose.

Note : je suis obligé de détacher la pièce jointe du fil pour cause de théorie personnelle

m@ch3

[increa]

On'a la représentation quadri-vectorielle ! , a=(,c), de pseudo-norme : 2c²-c²=c²:



càd :

et alors?
en déduisez vous que notre univers se déplace dans la quatrième dimension à la vitesse de 211985280 m/s ?

[increa]

le choix de la représentation quadri-vectorielle x(a,b) n'a aucun influence sur 'la réalité' des choses, un moyen sur lequel est projeter une idée ... , par exemple si tu prend C=c/V2 , si on remplace dans la relation du pseudo-norme de la RR (citer en haut) le facteur 1/V2 va disparaître ..., mais le problème où tu'as mesuré une vitesse de la lumière C=c/V2 ? (c :une constante imposer par la nature non pas par les maths ... ).

ps: la pseudo-norme s'en fou complètement de la constante qui s'y injecté ....(une relation mathématique)

et obtenir la compatibilité de la mécanique classique avec les phénomènes lumineux c'est pas important pour la constante injectée?

[azizovsky]

et alors?
en déduisez vous que notre univers se déplace dans la quatrième dimension à la vitesse de 211985280 m/s ?

J'ai voulu seulement trouver c/V2 à partir de la RR et pour entamer ce qui a suivait .....(sauf si j'ai perdu la raison..).

et obtenir la compatibilité de la mécanique classique avec les phénomènes lumineux c'est pas important pour la constante injectée?

je n'ai pas compris la question, la MC est remplacée par la RR, on touve la MC quand v<<<c, la composition des vitesses est remplacé par une composition relativiste...., on prend la pseudo-norme précédente, on la multiplie par m²c², on trouve la relation E²=(mc²)²+p²c² et on peut en déduire toutes les relations classiques avec des 'oublies' car mc² n'existe pas en MC....
et on peut aussi voir que les équations de Maxwell sont invariante dans les transformations de Lorentz(TL). (le cas classique cité par mach3.... ).
les TLs redonnent les Ts de Galilée pour v<<<c.
J'ai essayé de donner des réponses pour s'approcher un peu de la réponse ....

ps: il faut regarder une démonstration mathématique des TLs pour la constante....

[increa]

un commentaire la-dessus :



C'est la formule pour un cas très particulier : la chute d'un corps suivant l'axe y, avec le champ de gravitation suivant l'axe y, une coordonnée y et une vitesse suivant y nulle à l'origine des temps (on parlait justement de choix de repère ) et qui ne va donc s'appliquer correctement sur un grand intervalle de t et y que si g reste aligné sur l'axe y. Donc soit :
-c'est une chute radiale, donc inadapté pour la déviation de quoique ce soit (lumière ou pas) par un corps massif
-c'est une chute dans un champ de gravitation uniforme (par exemple causé par un plan infini) qui n'existe pas dans la réalité et qui est une approximation applicable pour un déplacement orthoradial très faible devant la distance radiale. Rien de remarquable concernant la lumière (ou tout autre corps très rapide) dans ces conditions, le déplacement orthoradial qui permet l'approximation est tellement petit que la "chute" de la lumière n'est même pas mesurable (faudrait faire le calcul sérieusement pour savoir quelle est la différence de prédiction entre mécanique classique et RG sur mettons 100m ou 1km, ça doit pas être bezef de toutes façons).

Bref, ce n'est pas avec cette formule que l'on montrera un désaccord entre la mécanique classique et l'expérience concernant la déviation de la lumière par les masses.


m@ch3

Pourtant c'est avec cette formule que je calcule avec succés la déviation d'un rayon lumineux au voisinage du soleil dans le premier texte de ce fil.
J'obtiens avec ce calcul une déviation moitié de celle observée...aussi pour une déviation double, il est logique de penser que pour obtenir la bonne valeur, il va falloir exposer la lumière à la gravitation un temps racine de deux fois plus important.
Ainsi il suffit de réduire la vitesse de la lumière d'un facteur racine(2) pour augmenter le temps d'exposition au champ gravitationnel.
Ce qui donnerait une vitesse de la lumière dans l'éther luminifère de c/racine de 2
Oui mais alors, pour mesurer la bonne mesure de c sur la terre il faut que mon temps propre soit aussi de racine de 2 par rapport au temps attaché à l'éther.
Ainsi la boucle est bouclée...
Le point de vue d'Einstein est exactement le même que le mien selon Lorentz sauf qu'Einstein s'est vissé le derrière sur l'éther luminifer sans le dire...
Aprés, facile de dire qu'il n'y a pas besoin de l'hypothèse de l'éther luminifère...

[jacknicklaus]

il est logique de penser que pour obtenir la bonne valeur, il va falloir exposer la lumière à la gravitation un temps racine de deux fois plus important. Ainsi il suffit de réduire la vitesse de la lumière d'un facteur racine(2) pour augmenter le temps d'exposition au champ gravitationnel.

Un membre de plus au club des génies incompris, et un fil qui approche de sa fermeture...

[mach3]

Mais en fait vous ne partez pas de gt²/2 qui n'est qu'une conséquence dans un cas particulier, vous partez de :
et de et vous projetez sur les axes x et y orthogonaux formant le plan contenant l'hyperbole, l'axe y passant par le centre du Soleil et l'axe x par le sommet de la trajectoire. Vous negligez la variation de vitesse suivant x (avec raison ici) ce qui permet de lier directement x et t, et donc considérer la moyenne suivant de la composante en y de g comme influence globale sur la vitesse en y.

On peut faire plus propre comme démarche, mais ça fonctionne.

Ce qui change en RG, si on garde cette démarche là, est simplement l'expression du vecteur g. Il ne dépend plus uniquement de l'inverse de r². De mémoire il y a un terme en l'inverse de r³, un terme dépendant de la vitesse radiale et un terme dépendant de la vitesse orthoradiale qui s'ajoutent (je vous retrouverais l'expression complète) et le vecteur obtenu n'est pas forcément radial.
On l'obtient via l'équation des géodésiques, qui dépend elle-même des coefficients de Christofell dont l'expression dépend du système de coordonnées utilisé.
Le plus simple ici est de travailler avec les coordonnées de Schwarzschild et d'utiliser l'expression de l'équation des géodésiques en fonction du temps coordonnée au lieu du temps propre :
(somme implicite sur les indices répétés, alpha et beta, de 0 à 3)
avec , et les Gamma majuscules avec indices haut et bas étant les coefficients de Christofell dont on peut trouver les expressions soit au bout de pages de calculs à partir de l'expression de la métrique, soit dans un ouvrage de référence (par exemple le catalog of spacetimes).

m@ch3

[increa]

Mais en fait vous ne partez pas de gt²/2 qui n'est qu'une conséquence dans un cas particulier,
m@ch3

Bonjour,

Si,l'équation 5 de ma démonstration, est la dérivée par rapport au temps de l'équation contestée.