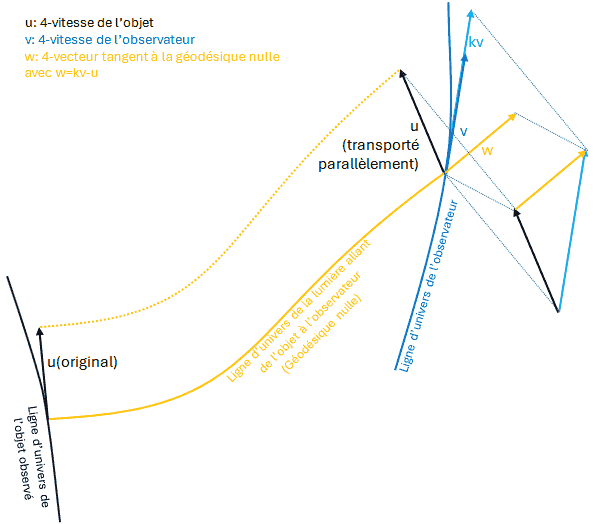
### cette discussion dérive du fil : https://forums.futura-sciences.com/q...tres-fort.html ###
La réponse de Gilgamesh me laisse perplexe quand il invoque l'expansion de l'univers pour expliquer la dilatation du temps
Que l'expansion modifie la longueur d'onde de la scène; ça c'est clair, mais la question porte sur le temps dont la mesure est modifiée par la gravitation.
Si l'on fait cuire l'oeuf (j'adore l'exemple) à proximité d'un trou noir (donc avec un champ gravitationnel intense) et que l'on observe la scène à une distance constante de 100 al. (donc là il n'y a pas d'expansion qui intervienne) L'observateur va bien mesurer que l'oeuf met plus que 3 mn à cuire ?
L'expansion crée une espèce de déplacement "apparent" puisque la distance entre deux points augmente au fil du temps (toutes choses égales par ailleurs) .
Du coup cette augmentation de la distance dans le temps génère une vitesse "apparente". En supposant la vitesse d'éloignement constante (ce qui n'est pas le cas en réalité) est ce que l'on a du coup un effet relativiste sur la mesure du temps ?
-----