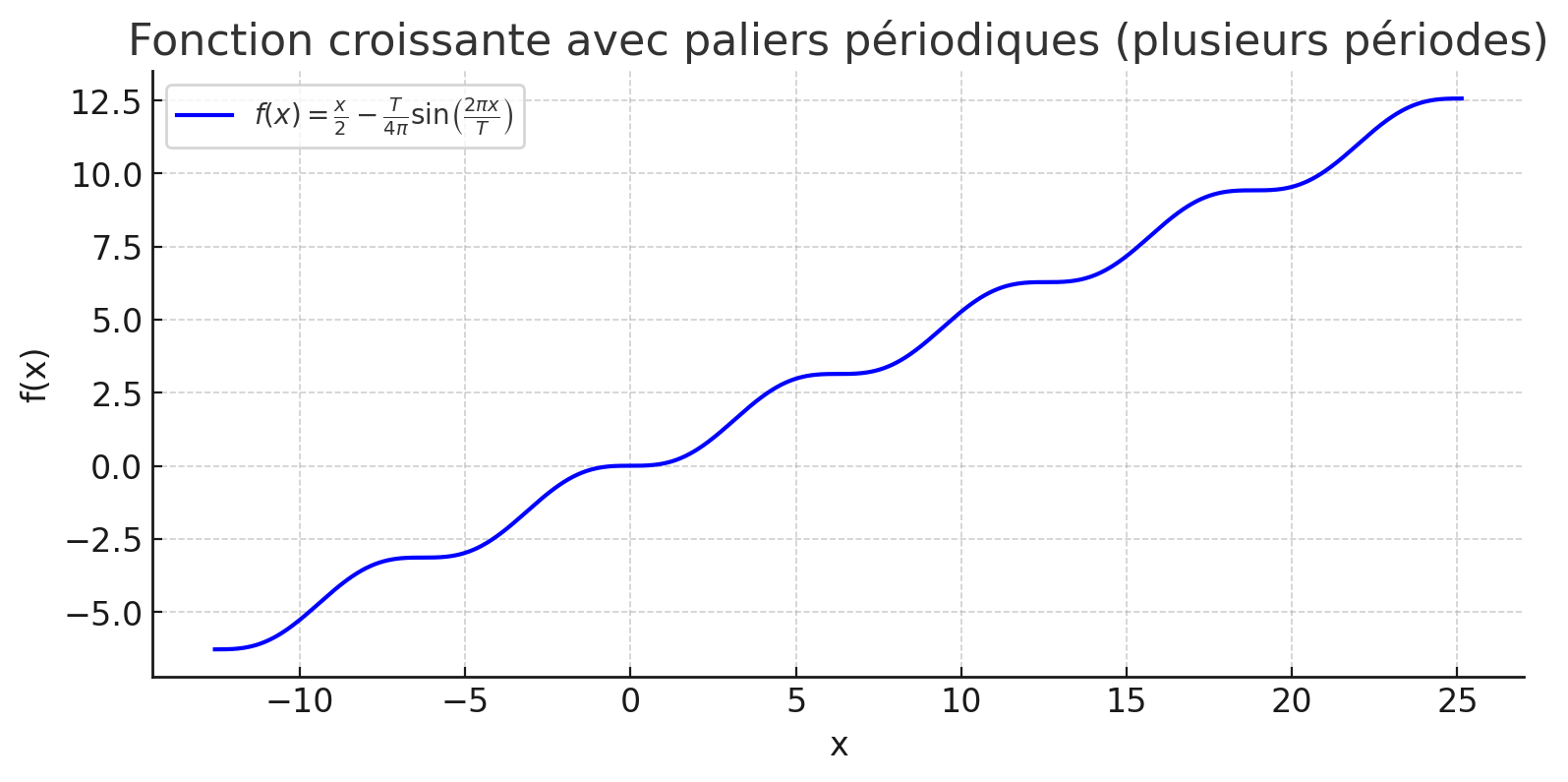
L'expansion en "escalier"
Discussions similaires
-
Par dwbh79 dans le forum Bricolage et décoration
Réponses: 3
Dernier message: 17/04/2023, 18h00
-
Par guynux dans le forum Bricolage et décoration
Réponses: 3
Dernier message: 11/02/2023, 19h36
-
Par invite0c5534f5 dans le forum Physique
Réponses: 4
Dernier message: 21/12/2021, 11h28
-
Par roy1360 dans le forum Bricolage et décoration
Réponses: 4
Dernier message: 22/07/2011, 21h49
-
Par invite89810102 dans le forum Habitat bioclimatique, isolation et chauffage
Réponses: 5
Dernier message: 20/04/2011, 10h00



 . C'est l'intégrale d'un sinus au carré, pour avoir une fonction croissante.
. C'est l'intégrale d'un sinus au carré, pour avoir une fonction croissante.