bonjour,
j'aimerais bien démonter que la fonction de transfert en boucle fermée de ce schéma s'ecrit ss la forme comme il est indiqué sur le schéma
merci bien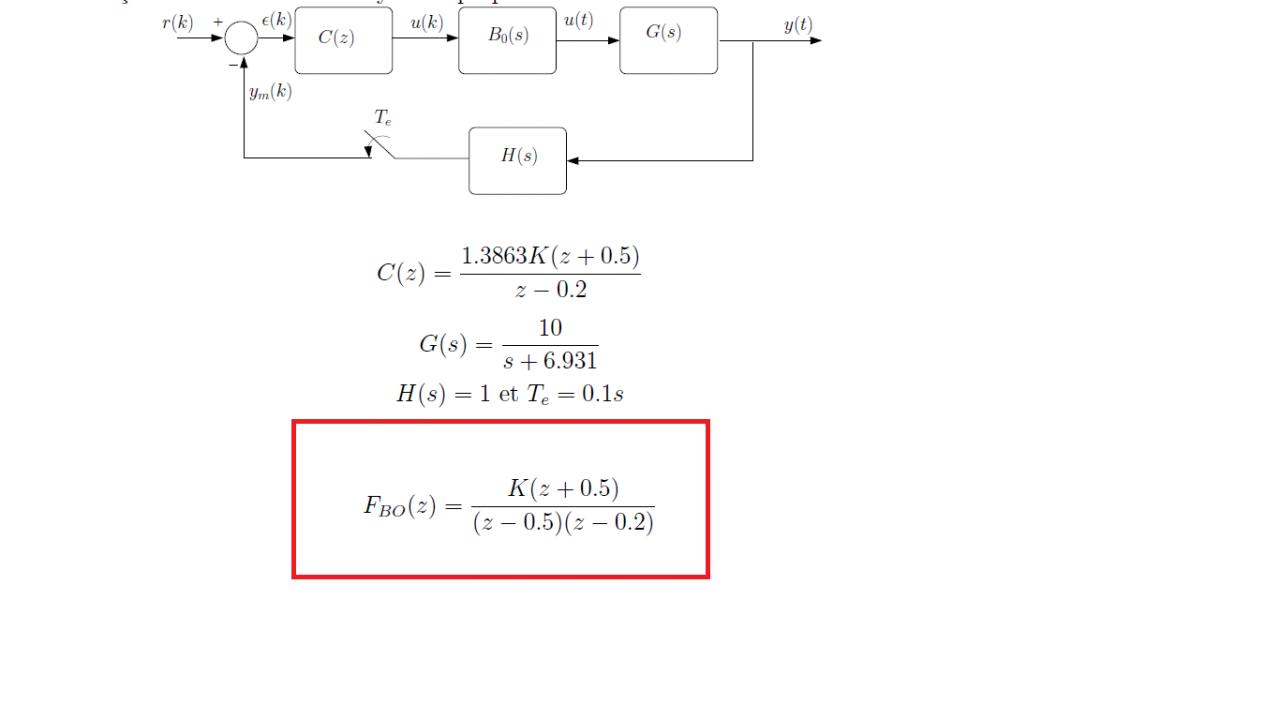
-----


bonjour,
j'aimerais bien démonter que la fonction de transfert en boucle fermée de ce schéma s'ecrit ss la forme comme il est indiqué sur le schéma
merci bien

A mon avis FBO(z) est la transformée en z du bloc B0(s). Il n'y a donc rien à démontrer dans ce que tu nous a donné.
A+

Non, Jack.
, c'est le bloqueur d'ordre 0.
Il faut trouver la boucle ouverte incluant ce bloqueur puis sans doute la BF.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».

Tu as raison. Au temps (autant?) pour moi.
A+


le problème c'est comment la trouver en boucle ouverte'
j'ai fait C(z) * la T en Z de ( (1/s) * G(s) ) mais je n'ais pas obtenu le résultat voulu
est ce que ce que j'ai fait est faux? sinon comment la trouver?
merci bien

Salut
La difficulté c'est de passer du monde physique au monde numérique, autrement dit, il te faut savoir passer d'une TZ à une TL... Plusieurs possibilités :
- Passer par le domaine temporel par une TZ inverse pour repasser en Laplace ensuite (en reconnaissant des formes simples, ou en utilisant des résultats mathématique de l'analyse complexe) : Z--->t--->s (long, théorique mais ça marche bien)
- Utiliser des tables de correspondance : http://lpsa.swarthmore.edu/LaplaceZT...FuncTable.html (simple et efficace...je recommande)
Dans ton cas, tu fais le produit de B0*G*H ... tu vas dans la table des correspondances, et tu en déduis la TZ de tout ça. Là tu multiples par C(z) qui fait partie de la BO, et ça te donne la FTBO.
Tu vois l'idée ?

PS : Attention ! comme B0 est un bloqueur d'ordre 0, il faudra non pas travailler avec B0*G*H mais avec 1/p*G*H (on ne prend pas la partie non linéaire de B0). Ensuite on multiplie la TZ trouvée par (1-z^-1) pour tenir compte de la partie non linéaire de B0(p). Cet artifice permet de travailler dans les tables avec des FT linéaires.


j'ai fait :
FTBO = C(z) * (1-z^-1) * TZ ( G(s) / s )
TZ ( G(s) / s ) = z / z+1 + z / z- e-6.931 T
et ça ne donne pas le bon résultat !!

Un peu de lecture s'impose pour acquérir la méthode :
http://www.femto-st.fr/~gonzalo.cabodevila/cours1A.pdf
De tête je tombe sur un truc qui a la même allure que le corrigé... il faut reprendre les calculs.

Bonjour,
Je comprends que tu veux parler du retard du bloqueur, mais c'est assez moche de dire "partie non linéaire".
(d'autant que 1/p, ce n'est pas linéaire non plus.)
Un bloqueur d'ordre 0 est linéaire.
Perso, j'aurais plutôt dit : la partie non fraction rationnelle, ou non polynomiale.
Cordialement.
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».

- Quand je t'ai lu j'ai eu un doute, puis je suis allé voir mon vieux cours où j'avais bel et bien écrit "partie non-linéaire"...Je comprends que tu veux parler du retard du bloqueur, mais c'est assez moche de dire "partie non linéaire".
Puis en réfléchissant, tu as raison car si on applique un terme exp(-pT) (un retard) à un signal a+b alors le résultat est le même que si on applique cet opérateur à a, puis b, et qu'on somme le résultat. En bref, la somme des "signaux retardés" c'est la même chose que la "somme des signaux" retardée...donc un bloqueur 0 est bel et bien linéaire.
- Le terme 1/p est bien un opérateur linéaire, car l'intégrale d'une somme c'est la somme des intégrales.
Du coup, je suis ok avec ceci :
MerciPerso, j'aurais plutôt dit : la partie non fraction rationnelle, ou non polynomiale.

Re,
Oui, 1/p est bien un opérateur linéaire, mais comme tu disais que le retard ne l'était pas, je ne savais pas trop de quelle linéarité tu causais.
T'avais noté "non linéaire" sur ordre du prof?
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».

Enfin je l'ai noté sans trop réfléchir, soit en recopiant un vendredi matin (donc sans réfléchir), soit en fonction de ce qu'a dit l'enseignant avec déformation des propos (ou pas)... difficile de dire de qui vient l'erreur. Ça remonte à 3 ans déjà.

