Conformateur à diode : comment éliminer mathématiquement les harmoniques d'un signal triangle ?

[black templar]

Bonsoir à tous.


J'aimerais transformer un signal triangulaire en un signal sinusoïdal. Pour cela, j'essaye de mettre en place un conformateur à diode.
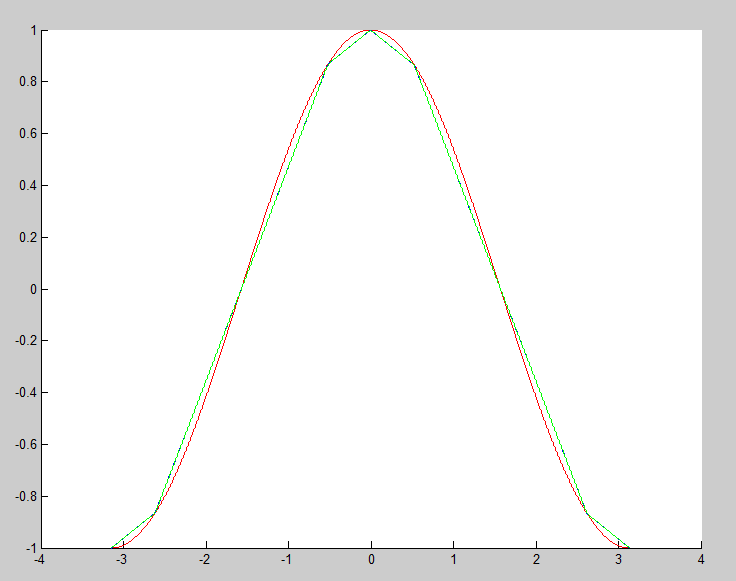
J'ai donc étudier le bouzin : le but, c'est d'approximer le sinus avec des bout de droites produit par des ponts diviseurs appliqué sur le triangle. Chaque bout de droite correspond à un pont diviseur précis qui est activé lorsque la tension d'entrée arrive à un certain seuil.
Les diodes servant à distinguer les alternances positives des négatives.
(le principe en animation : http://subaru.univ-lemans.fr/AccesLi.../conforme.html)

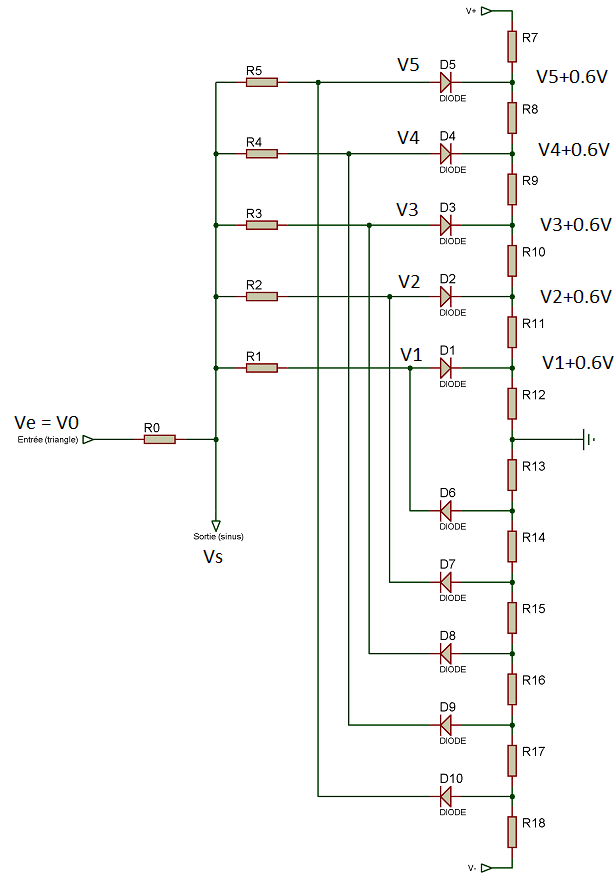
Le schéma du conformateur que je souhaite réaliser est le suivant :



J'ai donc

Avec n, le nombre de diodes activés
Vs la tension de sortie (sinus)
V0 le signal d'entrée (triangle)
V1 à Vn, les différents seuils d'activations


Je sais que mon signal triangulaire possèdes plusieurs harmoniques.
La première harmonique (fondamentale) est celle que je veux garder pour avoir un beau sinus
Il faut donc que j'élimine les harmoniques suivantes (3, 5, 7, 9, 12)
Je connais l'amplitude de ces harmoniques par rapport à la fondamentale (amplitude de l'harmonique n pour n impaire = 1/n^2)

Ma question, c'est comment faire pour lier les pentes de mes bouts droites aux harmoniques à annuler ?
Je ne vois pas comment faire :/


Quelqu'un aurait une idée de la façon de faire ?


Bonne soirée,
Black Templar
-----

[black templar]

A défaut de voir comment calculer les pentes et tensions seuils pour éliminer les harmoniques, j'ai fait quelques calculs pour trouver les pentes et tensions seuils pour se rapprocher visuellement d'un sinus.

Voici donc mon raisonnement :

Je veux conformer un triangle en sinus. Il me faut donc approximer d'abord mon sinus en bout de droites.

La première question que je me suis posé, c'est à quel moment changer de segment ? J'ai essayé de prendre des droites de durées équivalentes, mais là, on voit très clairement que le c'est certes précis au début du sinus (pour x = 0), mais qu'en fin de quart de sinus (x = pi/2), le signal est assez déformé et ne colle plus bien au sinus réel !
Je me suis donc dit que la durée de mes bouts de droites ne doit pas être proportionnel au temps lui même, mais plutôt à la pente de mon sinus. Pour trouver la pente du sinus, il suffit de le dérivé, ce qui nous donne cos(x).
Il suffit donc de trouver x pour (k est une constante qui vaut l'inverse du nombre de segments approximant le quart de période)

Ainsi, pour 3 segments, on a cos(x0) = 1 ; cos(x1) = 0.66 ; cos(x2) = 0.33 et cos(x3) = 0 (cos(x) représentant la pente du sinus)
Pour trouver à quel moment il faut commencer ou arrêter les segment, il faut donc prendre l'arccos des équations précédentes.
Ainsi x0 = 0 ; x1 = 0.85 ; x2 = 1.23 et x3 = 1.57 = pi/2. (Ici, le quart de période s'étale de 0 à pi/2)

En traçant les droites entre x0,x1 ; x1,x2 ; x2,x3 on obtient déjà une meilleure approximation visuelle du sinus.
Pour les pentes, je fais la moyenne des pentes du sinus en et soit,


J'ai mis en pj le rendu pour 3 segments par quart de période puis pour 5 segments par quart de période.
Le sinus est à 1hz, donc les x_i sont divisé par 2pi (pour normaliser tout ça vu que le quart de période n'est plus de pi/2 mais de 1/4).
En bleu, on a le triangle, en rouge, le sinus et en vert l'approximation par bout de segments pour 3 puis 5 segments.
L'amplitude max et min du sinus est pi/2 fois inférieur à l'amplitude max et min du triangle.

Que pensez-vous de cette méthode ? Y a-t-il plus performant pour avoir moins de distorsions ?
Avec ces calculs là, la pente en début de sinus (x=0) ne sera jamais de 1 et la pente au quart de période (x=pi/2) ne sera jamais 0 ... ça risque d'entrainer beaucoup de distorsion ??
Pour les discontinuités aux limites, elles seront gommés en pratique par la non linéarités des diodes...


Autre question au passage : existe-t-il d'autre types de conformateurs qui soient plus performant que celui à diodes ?? J'ai du mal à trouver les infos à ce sujet sur internet ...

++
Black Templar

[Tropique]

Bonjour,

ton approche est incontestablement intéressante. Par examen de la transformée de Fourier, on sait arriver à prévoir pour quels rapports cycliques d'impulsions on peut annuler certaines harmoniques.

Arriver à un résultat équivalent avec des segments de droite semble la continuation logique de ce principe, mais je crois que cela va être diaboliquement compliqué sur le plan mathématique, avec des intégrations d'équations transcendantes, et autres joyeusetés du genre.

Il est peut-être possible de trouver des raccourcis, mais je n'ai pas les compétences pour le faire.
Je crois que cela vaudrait la peine de poser la question à Gérard Michon de Final Answers, c'est le genre de problème qu'il affectionne, et j'ai déjà eu l'occasion de tester ses compétences.
http://www.numericana.com/answer/index.htm

Les méthodes d'optimisation habituelles de ces réseaux sont basées sur l'erreur d'amplitude: soit on s'arrange pour minimiser et égaliser les déviations de crête par rapport à l'idéal, soit on essaye de minimiser l'erreur globale par exemple par la méthode des moindres carrés.

Par contre, je n'ai jamais vu de méthode utilisant pour la conception le contenu harmonique. Après qu'une optimisation ait été choisie on calcule bien le niveau d'harmoniques, mais c'est différent.
Cela vaut certainement la peine de s'y interésser: j'ai déjà eu l'occasion de constater au cours de tests que la "plus belle" sinusoide vue en amplitude et dans le domaine temporel est loin d'être celle qui est la plus pure dans le domaine fréquentiel.

Parmi les autres méthodes, on peut citer le convertisseut trigonométrique universel, créé par Barrie Gilbert et basé sur ses principes de translinéarité.
C'est une méthode extrêmement puissante, capable d'une précision arbitrairement élevée, et qui peut convertir des angles beaucoup plus grands que 360°. L'AD639 utilise cette technique.
http://www.google.com/patents?id=EO8...page&q&f=false

Une autre possibilité est l'emploi d'une paire différentielle utilisée à niveau élevé.
La fonction de transfert "naturelle" est un sinus hyperbolique plutot que trigonométrique, mais avec quelques corrections et un bon "curve fitting", on peut arriver à des résultats exceptionnels.
Cette technique a été utilisée dans ce générateur, et elle permet de descendre sous 0.2%:
http://forums.futura-sciences.com/pr...ml#post1841145

On peut aussi employer d'autres éléments non-linéaires, FETs, MOS etc.

On peut également approximer l'arche de sinus par une parabole, avec un mise au carré.

Enfin, il y a plusieurs méthodes pour faire des conformateurs à diodes: celle que tu emploies, bien sûr, mais aussi des portes à diodes, qui fonctionnent "à l'envers": le gain est maximum quand toutes diodes conduisent, et quand il augmente, les différentes portes sebloquent successivement.
D'expérience, cette méthode donne de meilleurs résultats à moyens égaux que l'autre.

[black templar]

Bonjour Tropique !
Merci pour ta réponse.

Bonjour,

ton approche est incontestablement intéressante. Par examen de la transformée de Fourier, on sait arriver à prévoir pour quels rapports cycliques d'impulsions on peut annuler certaines harmoniques.

Arriver à un résultat équivalent avec des segments de droite semble la continuation logique de ce principe, mais je crois que cela va être diaboliquement compliqué sur le plan mathématique, avec des intégrations d'équations transcendantes, et autres joyeusetés du genre.

Sur le principe, c'est bien ce que je me suis dit. Essayer de faire correspondre les segments avec les harmoniques produite permettrait de bien dimensionner ces segments afin d'avoir une distorsion minimale.
Je me suis lancé dans les calculs, mais c'est d'un compliqué... Je n'arrive déjà pas avec deux segments ...

Il est peut-être possible de trouver des raccourcis, mais je n'ai pas les compétences pour le faire.
Je crois que cela vaudrait la peine de poser la question à Gérard Michon de Final Answers, c'est le genre de problème qu'il affectionne, et j'ai déjà eu l'occasion de tester ses compétences.
http://www.numericana.com/answer/index.htm

Oh, quel site énorme ! Je pense qu'avant de poser la question à Gérard Michon, je fais essayer d'avancé dans la modélisation et de bien comprendre ce que je fais...

Les méthodes d'optimisation habituelles de ces réseaux sont basées sur l'erreur d'amplitude: soit on s'arrange pour minimiser et égaliser les déviations de crête par rapport à l'idéal, soit on essaye de minimiser l'erreur globale par exemple par la méthode des moindres carrés.

Oui, mais qui dit que même en ayant une erreur très faible en temporel, la distorsion soit à l'image de cette erreur ?

Par contre, je n'ai jamais vu de méthode utilisant pour la conception le contenu harmonique. Après qu'une optimisation ait été choisie on calcule bien le niveau d'harmoniques, mais c'est différent.
Cela vaut certainement la peine de s'y interésser: j'ai déjà eu l'occasion de constater au cours de tests que la "plus belle" sinusoide vue en amplitude et dans le domaine temporel est loin d'être celle qui est la plus pure dans le domaine fréquentiel.

Hum... Je m'attaque peut-être à un trop gros morceau pour moi ... mais bon, je vais tenter, on verra bien ^^

Parmi les autres méthodes, on peut citer le convertisseut trigonométrique universel, créé par Barrie Gilbert et basé sur ses principes de translinéarité.
C'est une méthode extrêmement puissante, capable d'une précision arbitrairement élevée, et qui peut convertir des angles beaucoup plus grands que 360°. L'AD639 utilise cette technique.
http://www.google.com/patents?id=EO8...page&q&f=false

Vraiment intéressent ! Je ne savais pas que ce genre de chose existe ! Dans la datasheet de l'AD639, il y a même un montage qui converti du triangle en sinus !!
Bon, par contre, je ne le trouve pas chez mes revendeurs habituels...

Une autre possibilité est l'emploi d'une paire différentielle utilisée à niveau élevé.
La fonction de transfert "naturelle" est un sinus hyperbolique plutot que trigonométrique, mais avec quelques corrections et un bon "curve fitting", on peut arriver à des résultats exceptionnels.
Cette technique a été utilisée dans ce générateur, et elle permet de descendre sous 0.2%:
http://forums.futura-sciences.com/pr...ml#post1841145

Oui, j'ai déjà lu l'intégralité de ton projet et je m'en suis régalé (bien que j'ai décroché quand tu es passé à l'explication de ton étage d'amplification "à la Tropique" )

On peut aussi employer d'autres éléments non-linéaires, FETs, MOS etc.

On peut également approximer l'arche de sinus par une parabole, avec un mise au carré.

Enfin, il y a plusieurs méthodes pour faire des conformateurs à diodes: celle que tu emploies, bien sûr, mais aussi des portes à diodes, qui fonctionnent "à l'envers": le gain est maximum quand toutes diodes conduisent, et quand il augmente, les différentes portes sebloquent successivement.
D'expérience, cette méthode donne de meilleurs résultats à moyens égaux que l'autre.

Je vais regarder cet autre type de conformateur à diode. Si c'est plus performant et aussi simple, pourquoi s'en priver ^^



Merci d'avoir pris le temps de me répondre.
Je vais continuer à essayer de trouver un lien entre segments temporels et harmoniques.
Black Templar

[A voir en vidéo sur Futura]

[black templar]

Bon, une petite avancé : je viens de découvrir que les séries de Fourier, finalement, c'est utile !
J'ai donc laissé tombé la transformé de Fourier pour utilisé plutôt les séries afin de décomposer mes bouts de segments en une superposition de sinus.

La décomposition en série de Fourier d'un signal 2pi périodique est égal à

Il suffit donc de trouver les coefficients an et bn.

Reprenons la base : essayons d'approximer le sinus avec deux bouts de droite.
Pas très original car ça nous donne simplement un signal triangulaire en fait ^^ Mais sa décomposition en série de Fourier est simple !

On a donc notre signal triangulaire périodique f(x) = 1+x/pi pour x compris entre -pi et 0 et f(x) = 1 - x/pi pour x entre 0 et pi.

triangle.PNG

Le signal est paire (f(x) = -f(x)) donc les coefficients bn sont nul.
Pour le reste, on obtient pour n impair.
La décomposition du signal triangulaire en somme de sinus s'écrit donc
On en conclu donc qu'un signal triangulaire n'est rien d'autre qu'une superposition d'un cosinus à la fréquence fondamentale avec un harmonique 3 atténué d'un facteur 9, avec une harmonique 5 atténué de 25, etc.


J'ai donc repris le même raisonnement, mais avec 6 bouts de droites au lieu de 2 !
Cette fois-ci, la fonction f(x) est décomposé en 6 bouts de droites entre -pi et pi
f(x) = ax+b entre -pi et -g
f(x) = cx+d entre -g et -f
f(x) = ax+e entre -f et 0
f(x) = -ax+e entre 0 et f
f(x) = -ex+d entre f et g
f(x) = -ax+b entre g et pi

segments.PNG

Pareil, les bn sont nuls.

Pour les autres coefs, je trouve :




On pourra noter que si l'on prend a=c et b=d=e, on se ramène au cas précédent (approximation par un signal triangulaire) et que si l'on simplifie l'équation ci-dessus, on retombe bien sur a0 = 0 et an = les coef pour un signal triangle.
(ce qui est encourageant ^^)

Maintenant, la question, c'est trouver un moyen de déterminer les coefs a,b,c,e,d,f et g afin de minimiser les harmoniques et donc les an pour n>1
Bref, encore pas mal de boulot avant de savoir si les résultats seront concluant ou non :O

++
Black Templar

[jlcms]

Bonsoir,

J'ai parcouru la doc du AD639, et c'est assez impressionnant. En effet les harmoniques ont un niveau inférieur à -65dB par rapport au fondamental. Mon géné HP3325A ne fait pas tellement mieux. Les harmoniques sont donc à moins de 0.05% du fondamental.

@black templar
Dans ton modèle tu as considéré les diodes comme idéales.
Pourquoi ne pas avoir introduit la courbe caractéristique d'une diode avec I=Io(exp(Vj/Vo)-1), ce qui aurait eu pour effet de "casser" les angles et d'arrondir les plats?
Les calculs deviennent-ils trop pénibles?
Peut-on utiliser un développement limité du sinus et un développement limité du modèle, et en faire coller les coefficients?

[black templar]

Salut jlcms !

@black templar
Dans ton modèle tu as considéré les diodes comme idéales.
Pourquoi ne pas avoir introduit la courbe caractéristique d'une diode avec I=Io(exp(Vj/Vo)-1), ce qui aurait eu pour effet de "casser" les angles et d'arrondir les plats?
Les calculs deviennent-ils trop pénibles?

Déjà avec des bouts de droites, c'est pénible, alors je n'ose même pas imaginé avec cette équation !

Peut-on utiliser un développement limité du sinus et un développement limité du modèle, et en faire coller les coefficients?

Pas bête ça ! Je vais essayé comme ça aussi (dès que j'aurais fini de faire mumuse avec mon équation ) !

J'ai aussi pensé à utiliser les développements limités du sinus et du cosinus pour trouver une forme polynomiale qui s'approche de ces fonctions trigo (vu que l'intégrale d'un triangle est une parabole, je me suis dit qu'il y avait aussi quelque-chose à explorer de ce côté là ^^)

[Tropique]

Salut jlcms !


Déjà avec des bouts de droites, c'est pénible, alors je n'ose même pas imaginé avec cette équation !

Il ne faut négliger aucune piste: d'accord, avec des exponentielles, il y a 95% de chances que ça complique les choses de manière impossible, mais il y a également une opportunité de trouver des simplifications miraculeuses (et salvatrices):
N'oublions pas que la formule d'Euler relie les exponentielles aux fonctions trigonométriques.

On tombe parfois sur des gemmes inattendues, mais il faut tout explorer et rester à l'affut de la bonne surprise (si si ça arrive, même à moi ça m'est déjà arrivé!), et la reconnaitre pour telle lorsqu'elle se présente (peut-être la partie la plus difficile, paradoxalement).

[black templar]

Il ne faut négliger aucune piste: d'accord, avec des exponentielles, il y a 95% de chances que ça complique les choses de manière impossible, mais il y a également une opportunité de trouver des simplifications miraculeuses (et salvatrices):
N'oublions pas que la formule d'Euler relie les exponentielles aux fonctions trigonométriques.

On tombe parfois sur des gemmes inattendues, mais il faut tout explorer et rester à l'affut de la bonne surprise (si si ça arrive, même à moi ça m'est déjà arrivé!), et la reconnaitre pour telle lorsqu'elle se présente (peut-être la partie la plus difficile, paradoxalement).

J'essayerais.

Sinon, j'ai "informatisé" ma formule précédente pour pouvoir générer de jolies courbes (merci Matlab !)
J'ai trouvé une coquille dans mon coef a0, une erreur de recopiage à la fin de mon calcul -_- (les coef 1/2 avaient disparues !)

Je remet donc la formule des a0 :


J'ai donc simulé tout ça en prenant les coefficients qui vont bien pour retrouver un signal triangle simple.
J'ai donc a = c = 2/pi ; b = d = e = 1 et f = g = pi/2
Magie, la formule que j'ai trouvé pour retrouver la décomposition en série de Fourier marche bien, je retrouve mon triangle. Jusque là, tout va bien. (taux de distorsion de 0.1212)

decomposition_serie_f_2.png

Par contre, quand je prend un signal autre qu'un triangle, et bien j'ai quelques problèmes ...
Exemple avec f = arcsin(0.5) ; g = pi - f ; a = (1 - cos(f))/f ; b = a.pi - 1 ; c = 2.cos(f)/(pi-2f) ; d = c.pi/2 ; e = 1
La courbe bleu permet de visualiser l'approximation du sinus avec les coefs ci-dessus et la courbe verte, c'est sa décomposé de Fourier. Et bien on remarque que les pentes ont l'air correctes, mais pas l'offset...
Conclusion : il doit y avoir une erreur de signe quelque part dans mon équations (parce que là, un taux de distorsion de 1.8131 c'est pas top)

decomposition_serie_f.png

[black templar]

Arf ... double post, je vais me faire taper sur les doigts
(J'ai trouvé l'erreur plus vite que prévu ^^)

J'ai trouvé un peu au hasard les erreurs de signes. Maintenant ça marche. Je vais refaire un tour du côté de mes intégrales pour être sur, mais avec la nouvelle formule ci-dessous, il n'y a plus de problème !





Taux de distorsion de 0.0421, c'est mieux XD


Pour ceux que ça intéresse, je met le code matlab !

 Cliquez pour afficher

close all;
clear all;
clc;

fe = 5000; % fréquence d'échantillonnage
temps = 7; % temps total de mesure en seconde
t=(-temps/2:1/fe:temps/2-1/fe); % centrage sur 0

sinus = cos(t(:));  % Cosinus de référence d'amplitude 1

% Coefficients de ma fonction
f = asin(0.5);
g = pi-f;
a = (1-cos(f))/f;
b = a*pi-1;
c = 2*cos(f)/(pi-2*f);
d = c*pi/2;
e = 1;

% Pour un triangle
% b = 1;
% d = b;
% e = b;
% a = 2/pi;
% c = a;
% f = pi/2;
% g = f;

% Fonction à décomposer en série de Fourier
fonction_segments_ordre2 = zeros(1,temps*fe); 
for k=0 : f*fe
    % de -f à 0
    x = k/fe-f;
    fonction_segments_ordre2(1,round(k+temps*fe/2-f*fe)) = e+x*a;
    % de 0 à f
    x = k/fe;
    fonction_segments_ordre2(1,round(k+temps*fe/2)) = e-x*a;
    
    % de -pi à -g
    x = k/fe-pi;
    fonction_segments_ordre2(1,round(k+temps*fe/2-pi*fe)) = b+x*a;
    % de g à pi
    x = k/fe+g;
    fonction_segments_ordre2(1,round(k+temps*fe/2+g*fe)) = b-x*a;
end
for k=0 : (g-f)*fe
    % de -g à -f
    x = k/fe-g;
    fonction_segments_ordre2(1,round(k+temps*fe/2-g*fe)) = d+x*c;
    % de f à g
    x = k/fe+f;
    fonction_segments_ordre2(1,round(k+temps*fe/2+f*fe)) = d-x*c;
end


somme_quad_harmoniques = 0;         % Somme quadratique des coefficents
serie_fourier_fonction_segment_ordre2 = zeros(1,temps*fe);  

% Calcul du coef a0
a0 = ((f^2-g^2)*(c-a)/2 + f*(e-d) - g*(b-d) - pi^2*a/2 + pi*b)/pi;
serie_fourier_fonction_segment_ordre2 = serie_fourier_fonction_segment_ordre2 + a0;

% Calcul des harmoniques
for n=1:2500
    an = (c-a)/n*(g*sin(n*g)-f*sin(n*f)) + (c-a)/n^2*(cos(n*f)-cos(n*g)) + (d-e)/n*sin(n*f) - (d-b)/n*sin(n*g) + a/n^2 - a/n^2*(-1)^n;
    an = an / pi * 2;
    an*pi^2/8;
    
    serie_fourier_fonction_segment_ordre2(1,:) = serie_fourier_fonction_segment_ordre2(1,:) + an*cos(n*t(1,:));
    
    % Somme quadratiques des coefs > 2
    if n == 1
        a1 = an;
    else
        somme_quad_harmoniques = somme_quad_harmoniques + an^2;
    end
end

% Calcul du taux de distorsion
taux_distorsion = sqrt(somme_quad_harmoniques)/a1;
taux_distorsion


% Affichage des graphiques
hold on;
plot(t,sinus(:),'r');
plot(t,fonction_segments_ordre2(:),'b');
plot(t,serie_fourier_fonction_segment_ordre2(:),'g');





%%% Autres tests


% triangle = zeros(1,temps*fe);   % Signal triangulaire (100 premières harmoniques)
% for i=1:100
%     triangle(1,:) = triangle(1,:) + 8/pi^2*cos(t(1,:)*(2*i-1))/(2*i-1)^2;
% end
% 
% signal = triangle;              % Signal triangulaire sans les harmoniques 3 5 7 9 et 11
% for i=2:6
%     signal(1,:) = signal(1,:) - 8/pi^2*cos(t(1,:)*(2*i-1))/(2*i-1)^2;
% end
% signal = signal*pi/4;           % Atténuation de pi/4
% 
% rectangle = zeros(1,temps*fe);   % Signal rectangulaire (100 premières harmoniques)
% for i=1:100
%     rectangle(1,:) = rectangle(1,:) + 4/pi*sin(t(1,:)*(2*i-1))/(2*i-1);
% end

%plot(t,triangle(:),'b');
%plot(t,signal(:),'g');
%plot(t,rectangle(:),'b');

++
Black Templar