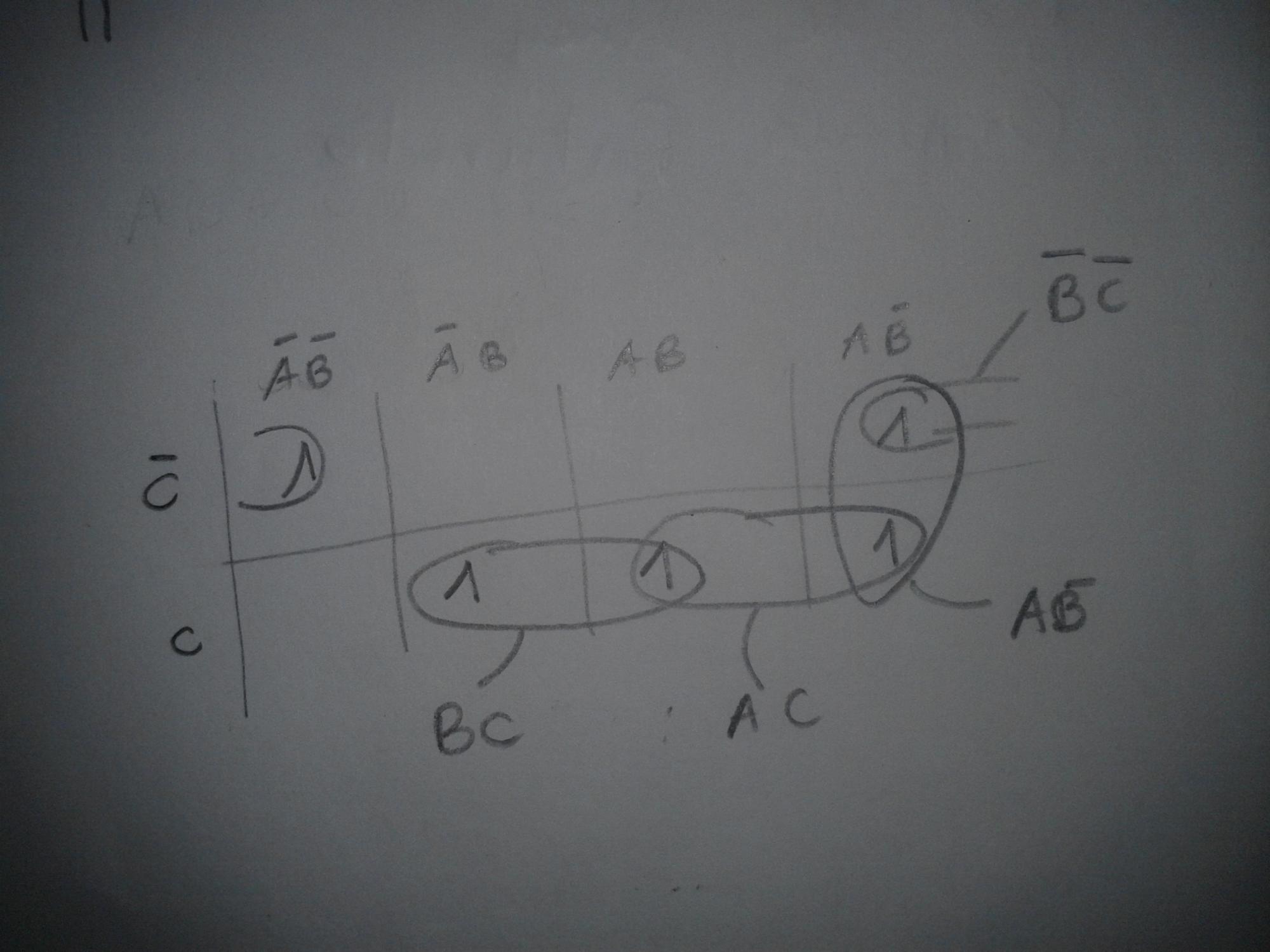
Bonsoir tout le monde! Je fais appel à vous pour un exercice sur le théorème de DeMorgan.
Si vous pouviez me corriger pour les deux premières ce serait cool
Capture3.PNG
Capture1.PNG
Autre exo :
Ici je dois démontrer que les deux expressions sont égales mais j'ai du mal à comprendre le principe :
Capture.PNG
J' aurais aimé vouloir t' aider mais le soucis est que je n' arrive pas à ouvrir tes pièces jointes ^^'
Ah mince je vais les reposter tout de suite alors
Il suffit d'attendre que les pièces jointes soient validées
En général ça va assez vite
#images hébergées sur serveur externe supprimées.
Merci de se conformer aux consignes suivantes:
http://forums.futura-sciences.com/el...-sabonner.html
Si tu pouvais me corriger pour les deux premières s'il te plait et m'expliquer la méthode pour la troisième.
Merci beaucoup!
Dernière modification par Jack ; 03/03/2013 à 00h53.
ça me rappelle le bon vieux temps ^^
On t' a dit que c' était faux?
Non on m'a pas dit que c'était faux mais je suis pas sûr d'avoir bon en fait, j'ai lu le cours mais je sais pas si je l'ai bien compris ^^
Pour le deuxième cas, il existe une méthode simple, le tableau de karnaugh, je ne sais pas trop si tu l' as déjà employé, entendu ^^' rien qu' avec cette méthode (qui nous prend 3 secondes), j' ai trouvé une erreur, le résultat est BC + AC + A/B + /B/C
Pour le premier cas, ce qu' il manquerait (je pense..) c' est les parenthèses: (/A + /B + /C) . (/D + /E + /F)
Malheureusement non ^^ on a pas encore vu le tableau de karnaugh, qu'est-ce que c'est exactement ?
sinon l'expression 1 et 2 sont bonnes ?
#images hébergées sur serveur externe supprimées.
Merci de se conformer aux consignes suivantes:
http://forums.futura-sciences.com/el...-sabonner.html
Je reposte les images car je me suis trompé dans les liens en haut désolé
Dernière modification par Jack ; 03/03/2013 à 00h53.
ouch c' est plus compliqué le premier lien mdr, et d' ailleurs la méthode de karnaugh ne s' applique pas dans ces cas là...
Mdr c'est pas grave je vais essayer de comprendre, merci pour ton aide et si tu as une idée n'hésite pas ^^
ça m' a l' air juste les deux liens que tu viens de m' envoyer
à moins que pour le deuxième lien, il faut mettre les parenthèses: (/A + /B + /C) . (/D + /E + /F)
Voilà une photo montrant la méthode par résolution du tableau de karnaugh, je sais que l' image n' est pas au top, j' espère tout de même que tu comprends le fonctionnement à travers cette photo ^^'
Voici le fonctionnement: on a trois variables A, B et C donc comme tu peux le voir sur la photo, j' ai regroupe A et B ensemble et laissé C seul, ensuite j' ai mis tous les états possibles (attention l' ordre dans lequel j' ai placé les états sont importants!!) ensuite je mets les 1 en fonction de l' équation:
ton équation est la suivante: /ABC + A/B/C + /A/B/C + A/BC + ABC , dans le tableau, le premier 1 tout en haut à gauche correspond à /A/B/C soit le troisième terme de ton équation. En résumé chaque 1 du tableau correspond à un terme de l' équation.
Comme tu peux le constater, j' ai fait des regroupements, on ne peut le faire que par 2, 4, 9 etc et dans ce regroupement, tu ne gardes que les variables qui ne changent pas d' état ^^
voili voilou j' espère que j' ai été clair dans l' explication, si tu as besoin de d' autres renseignements ou quoi que ce soit, n' hésites pas
