Résoudre un circuit RC

[omega7130]

Bonsoir,

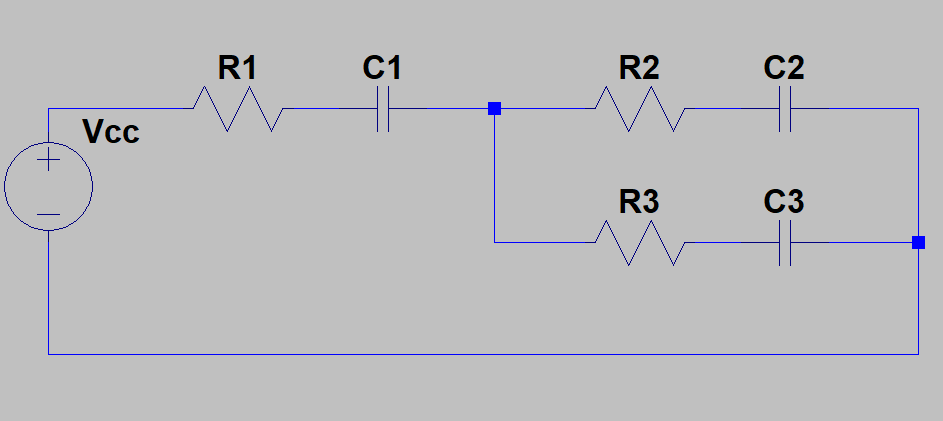
J'ai besoin d'aide pour résoudre le circuit suivant :

Vcc -----|R1|---|C1|---|R2|---|C2|----- GND
                               |          |
                              -|R3|---|C3|-

J'utilise les lois de kirchhoff pour modéliser le systéme et j'obtient :

IR1 = IR2 + IR3
Vcc = UR1 + UC1 + UR2 + UC2
UR2 + UC2 = UR3 + UC3

Je remplace les termes afin d'obtenir un systéme de 3 équations à 3 inconnues :

dUC1   C2    dUC2    C3   dUC3
____ = __ * ______ + __ * ____
 dt    C1     dt     C1    dt


dUC2    Vcc       R1*C1   dUC1      1             1
____ = _______ - _____ * ______ - _____ * UC1 - ______ * UC2
 dt     R2*C2     R2*C2    dt     R2*C2         R2*C2


dUC3   R2*C2   dUC2
____ = _____ * ____ + UC2 - UC3
 dt    R3*C3    dt

C'est ici que je reste bloqué, je n'arrive pas à résoudre le systéme.
Auriez-vous une solution à me proposer s'il vous plait ?

Bien à vous,
-----

[omega7130]

Il y'a eu un problème d'affichage et je n'arrive pas à éditer le message.

Voici le schéma :



J'ai réécrit les équations :

(dUC1/dt) = (C2/C1) * (dUC2/dt) + (C3/C1) * (dUC3/dt)
(dUC2/dt) = (Vcc/(R2*C2)) - ((R1*C1)/(R2*C2)) * (dUC1/dt) - (1/(R2*C2)) * UC1 - (1/(R2*C2)) * UC2
(dUC3/dt) = ((R2*C2)/(R3*C3)) * (dUC2/dt) + UC2 - UC3

[f6bes]

Bjr à toi,
Ton shéma indique que le générateur est une tension continue. Je vois mal du continu
pouvoir passer à travers un condensateur.
Donc aucun courant ne peut circuler.
Bonne journée

[Patrick_91]

Bonjour,

on shéma indique que le générateur est une tension continue. Je vois mal du continu
pouvoir passer à travers un condensateur.
Donc aucun courant ne peut circuler.

Il te manque l'intérrupteur qui se ferme à T0 c'est ça !
A plus

[A voir en vidéo sur Futura]

[Antoane]

Bonjour,

Personnellement, je l'ai plutôt fait en complexes : c'est plus lisible et simplifie les équations - quitte à revenir à l'équation différentielle après coup.

> Je remplace les termes afin d'obtenir un système de 3 équations à 3 inconnues
Et comme ces équations sont linéaires et indépendant, la solution existe. Reste à secouer les équations pour que ca marche
L'idée étant de faire ressortir une équation différentielle n'impliquant qu'une unique grandeur électrique, e.g. i₁, u₁, ou autre.

> (dUC3/dt) = ((R2*C2)/(R3*C3)) * (dUC2/dt) + UC2 - UC3
cette équation n'est pas homogène, elle est donc fausse.

[f6bes]

Bonjour,



Il te manque l'intérrupteur qui se ferme à T0 c'est ça !
A plus

Bjr à toi,e en tension
Dans ce cas , ça change pas mal de chose ( temps de montée en tension.....)
Bonne journée

[Patrick_91]

Hello,

Il manque aussi les états de charge initiales des capas ... on suppose "0" ...
Et on applique un echelon de tension a l'instant T0 ...
A plus

[Antoane]

Bonjour,

Condition initiales et allure de Vcc ne changent pas grand chose à la mise en équation - en tout cas tant qu'il ne devient pas nécessaire de dériver ou d'intégrer Vcc.
C'est lors de la résolution de l'équation différentielle que la question se posera vraiment.

[Patrick_91]

Hi
Oui mais dit autrement , si non F6BES a raison en l'état les courants sont nuls , les capas déchargées for ever ...
ce qui ne change rien a l’équation mais permet de ne pas commencer les calculs ..

A plus

[omega7130]

Bonjour,

Je vous remercie pour vos réponses.

Bjr à toi,
Ton shéma indique que le générateur est une tension continue. Je vois mal du continu
pouvoir passer à travers un condensateur.
Donc aucun courant ne peut circuler.
Bonne journée

Hi
Oui mais dit autrement , si non F6BES a raison en l'état les courants sont nuls , les capas déchargées for ever ...
ce qui ne change rien a l’équation mais permet de ne pas commencer les calculs ..

A plus

Le courant ne traverse pas le condensateur, mais des charges électrique quittent la borne positive et d'autres rejoignent la borne négative.
J'ai réalisé une simulation avec LTSPICE et IR1, IR2, IR3 ne sont pas nuls, les condensateurs se chargent en ~10ms.

Bonjour,
Il te manque l'intérrupteur qui se ferme à T0 c'est ça !
A plus

Oui vous avez raison, il y'a un interrupteur simple raccordé en série avec le générateur, celui-ci se ferme à t=0s et reste fermé.
Je cherche à déterminer le courant et la tension aux bornes de chaque composants à chaque instant du temps.

Bonjour,
Personnellement, je l'ai plutôt fait en complexes : c'est plus lisible et simplifie les équations - quitte à revenir à l'équation différentielle après coup.

Je sais qu'il est possible de résoudre des circuit alimenté en tension sinusoidale avec les nombres complexes.
Par contre, je ne sais pas comment les utiliser pour résoudre des circuits alimenté par une tension continue.
Auriez-vous un exemple s'il vous plait ?

> (dUC3/dt) = ((R2*C2)/(R3*C3)) * (dUC2/dt) + UC2 - UC3
cette équation n'est pas homogène, elle est donc fausse.

Oui vous avez raison, j'ai corrigé la formule : (dUC3(t) / dt) = ((R2 * C2)/(R3 * C3)) * (dUC2(t) / dt)) + (UC2(t) / (R3 * C3)) - (UC3(t) / (R3 * C3))

Hello,
Il manque aussi les états de charge initiales des capas ... on suppose "0" ...
Et on applique un echelon de tension a l'instant T0 ...
A plus

Le circuit est alimenté avec une tension continue, l'interrupteur en série avec le générateur se ferme à t=0s.
C1, C2 et C3 valent 0V à t=0s.

> Je remplace les termes afin d'obtenir un système de 3 équations à 3 inconnues
Et comme ces équations sont linéaires et indépendant, la solution existe. Reste à secouer les équations pour que ca marche
L'idée étant de faire ressortir une équation différentielle n'impliquant qu'une unique grandeur électrique, e.g. i₁, u₁, ou autre.

J'ai réussis à écrire un systéme de 3 équations mais je ne sais pas si il est valide, voici les détails de mon calcul :

Je cherche :
IR1(t), IR2(t), IR3(t), UR1(t), UR2(t), UR3(t)
IC1(t), IC2(t), IC3(t), UC1(t), UC2(t), UC3(t)

Mise en équation du circuit :
Loi des noeuds :
IR1(t) = IR2(t) + IR3(t)

Loi des mailles :
Vcc = UR1(t) + UC1(t) + UR2(t) + UC2(t)
UR2(t) + UC2(t) = UR3(t) + UC3(t)

Loi d'ohms :
IR1(t) = UR1(t) / R1 = IC1(t) = dQC1(t) / dt = C1 * (dUC1(t) / dt)
IR2(t) = UR2(t) / R2 = IC2(t) = dQC2(t) / dt = C2 * (dUC2(t) / dt)
IR3(t) = UR3(t) / R3 = IC3(t) = dQC3(t) / dt = C3 * (dUC3(t) / dt)

UR1(t) = R1 * IR1(t) = R1 * C1 * (dUC1(t) / dt)
UR2(t) = R2 * IR2(t) = R2 * C2 * (dUC2(t) / dt)
UR3(t) = R3 * IR3(t) = R3 * C3 * (dUC3(t) / dt)

Je remplace les termes du systéme afin de réduire le nombre d'inconnues :
C1 * (dUC1(t) / dt) = C2 * (dUC2(t) / dt) + C3 * (dUC3(t) / dt)
UR2(t) = Vcc - UR1(t) - UC1(t) - UC2(t)
UR3(t) = UR2(t) + UC2(t) - UC3(t)

(dUC1(t) / dt) = (C2/C1) * (dUC2(t) / dt) + (C3/C1) * (dUC3(t) / dt)
R2 * C2 * (dUC2(t) / dt) = Vcc - (R1 * C1 * (dUC1(t) / dt)) - UC1(t) - UC2(t)
R3 * C3 * (dUC3(t) / dt) = (R2 * C2 * (dUC2(t) / dt)) + UC2(t) - UC3(t)

Je réecrit les équations en fonction de dUC :
(dUC1(t) / dt) = (C2/C1) * (dUC2(t) / dt) + (C3/C1) * (dUC3(t) / dt)
(dUC2(t) / dt) = (Vcc/(R2 * C2)) - ((R1 * C1)/(R2 * C2)) * (dUC1(t) / dt)) - (UC1(t)/(R2 * C2)) - (UC2(t)/(R2 * C2))
(dUC3(t) / dt) = ((R2 * C2)/(R3 * C3)) * (dUC2(t) / dt)) + (UC2(t) / (R3 * C3)) - (UC3(t) / (R3 * C3))

C'est ici que je bloque, je ne trouve pas de méthode pour résoudre ce système.

[mizambal]

Hey, est ce que : "appliquer la transformation de Laplace, faire de toussa une matrice puis essayer de la diagonaliser (via matlab ou autre soft)" pourrait marcher dans ton cas ?

[Antoane]

Bonjour,



> est ce que : "appliquer la transformation de Laplace, faire de toussa une matrice puis essayer de la diagonaliser (via matlab ou autre soft)" pourrait marcher dans ton cas ?
Il s'agit de résoudre un set d'équations linéaires (affines) donc la technique, même si elle est sale et lourde, fonctionne.
C'est ce que je proposais plus haut lorsque je parlais de passer par les complexes et c'est ainsi que j'ai résolu l'exo de mon côté
Ceci dit, la matrice n'est que de dimension 3 et initialement presque creuse, elle est donc assez aisément digonalisable à la mains.

Je sais qu'il est possible de résoudre des circuit alimenté en tension sinusoidale avec les nombres complexes.
Par contre, je ne sais pas comment les utiliser pour résoudre des circuits alimenté par une tension continue.

Laplace, Fourier, les complexes... c'est tout pareil
Il s'agit finalement de résoudre l'ensemble d'équations différentielles dans le domaine de Laplace, puis d'en déduire la fonction associée dans le domaine temporel.

Voir par exemple : https://fr.wikipedia.org/wiki/Applic...3%A9rentielles, http://perso.iut-nimes.fr/flouchet/M...%20laplace.pdf, etc.

[mizambal]

C'est certain que ça reste faisable à la main mais la flemme quoi d'ailleurs je me suis gourré de suggestion de logiciel je voulais dire Maple, sinon un de ses équivalent gratuit : Xcas ou Maxima

Par contre à l'école j'ai jamais utiliser de nombres complexes pour le DC. Uniquement avec du AC. Surement que les enseignants ont une raison à cela, car après tout pour un électricien il n'est pas aberrant de remplacer p (ou S en anglais) par j.w et inversement.

J'ai tout de mm l'impression que cette gymnastique ( temporel -> fréquentiel -> temporel) induit parfois des erreurs dans les simu genre LTSpice. Par exemple je ne trouve de pointe de courant au démarrage dans un condensateur de 150nF attaqué par un cosinus du genre SINE(0 325 1 0 0 90) , c'est pourtant pas un circuit très compliqué sniff pas de pointe de courant au démarage .asc .txt

[omega7130]

Bonjour,

Encore merci pour vos réponses.
Si j'ai bien compris, je transforme mes 3 équations à l'aide de Laplace, et je mais le tout dans une matrice que je diagonalise.

J'ai encore du boulot
Bien à vous,