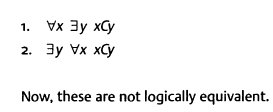Equivalence

[BIG136]

Bonjour,
Je suis en train de lire le livre: Logic A very short introduction de Graham Priest et en page 22 je tombe sur:



Est-ce que ces deux expressions sont équivalentes?

Si non, pour quoi?

Pour moi oui car:
1-pour tout x , il existe un y tel que x est causé par Y.
2-il existe un y pour tout x, tel que x est causé par Y.
D'avance merci.
-----

[Deedee81]

Salut,

2-il existe un y pour tout x, tel que x est causé par Y.

Ca c'est faux (ou mal exprimé). Il faudrait dire :
"Il existe un y, tel que : pour tout x...."

Et là ce n'est plus équivalent car dans la première expression, on dit que pour tout x il existe un y mais pas nécessairement le même pour chaque x.

Exemple :
"Pour toute porte il existe une clef tel que "la clef permet d'ouvrir la porte".
Et
"Il existe une clef telle que pour toute porte, cette clef ouvre la porte".

Le premier implique juste que chaque porte a une clef qui lui convient. La deuxième c'est le passe partout universel.

[BIG136]

Bonjour et merci.

D'après votre explication ,je comprends que dans 1, c'est "for every x" , et dans 2, c'est "for all x".

Cordialement.

[Deedee81]

En français (ou en anglais) c'est vrai que c'est un peu ambigu mais oui je pense qu'on peut le traduire comme ça.

[A voir en vidéo sur Futura]

[Tryss2]

Sur un exemple mathématique simple :



=> Il existe un nombre réel qui est l'opposé de tout les nombres

La première expression se traduit par "Tout nombre réel a un opposé"
La seconde se traduit par "Il existe un nombre réel qui est l'opposé de tout les nombres"

[Médiat]

Bonjour,

Pour compléter ce qui a été dit, d'abord un exemple (chacun a son favori)
En arithmétique
qui exprime que pour chaque élément (les entiers par exemple), il existe un élément plus grand (il suffit de penser à , pour voir que ceci est vrai)
qui exprime qu'il existe un élément plus grand que tous les autres (ce qui est clairement faux (dans IN par exemple))

D'un façon générale , peut s'écrire différemment : en posant

Alors que , en posant , s'écrit , ces deux formules ne peuvent être logiquement équivalente.

Lorsque vous avez plusieurs quantificateurs qui se suivent (en forme prénexe), chaque variable peut dépendre des précédentes, mais en fait ceci n'est significatif que dans le cas de l'alternance , par contre est bien la même chose que