Concours Général de Mathématiques 2010 !!

[invite6c146f6c]

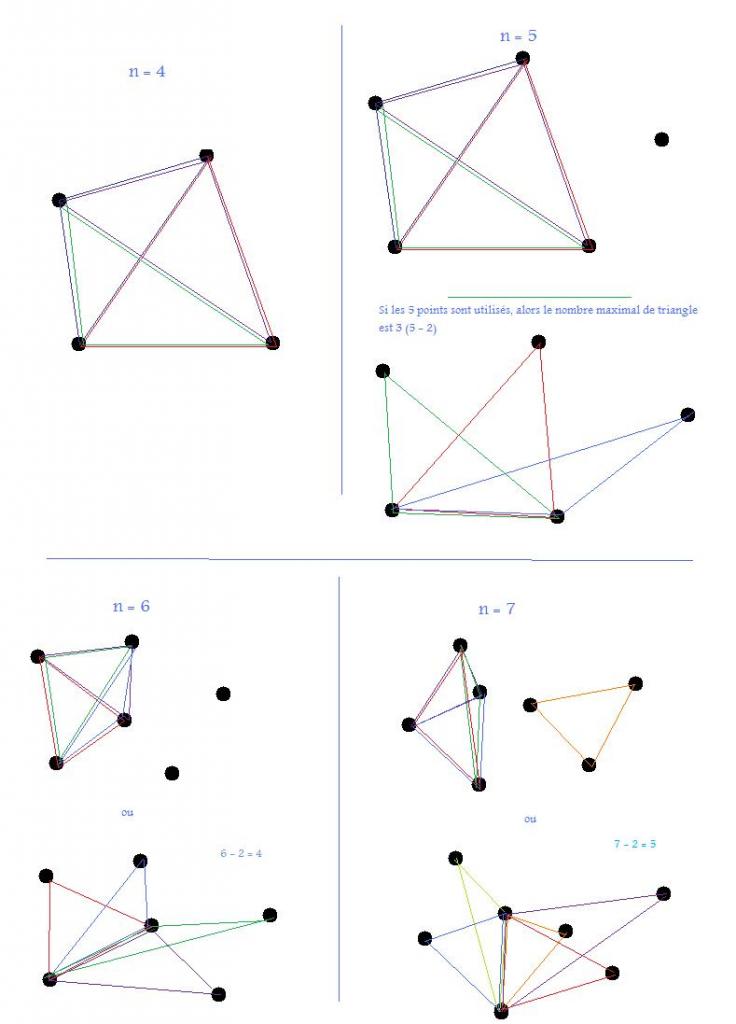
Bonsoir,

J'ai passé le concours général de 9h à 14h aujourd'hui, je ne suis pas le seul (j'imagine) et j'aimerai savoir ce que ceux qui l'ont passé en on pensé ?....

Pour ma par n'ayant vu que partiellement les probabilités les soirs chez moi environ 1 semaine avant j'ai trouvé l'exercice 3 particulièrement dur, l'exo 1 beaucoup plus abordable malgré la difficulté (dernière question pas beaucoup d'idées ) et le 2 le temps ma largement manqué (les idées aussi un peu ^^)

voila, si certains veulent le sujet demandé je peut le mettre à disposition..
-----

[inviteedc967b3]

Hey!
Je l'ai passé aussi et j'ai vraiment trouvé ça difficile, et particulièrement l'exercice 2! Je n'ai toujours pas trouvé le "truc" donc si tu as eu le temps de démonter un peu cette histoire de triangles, n'hésite pas à poster tes découvertes!

[invite31dc2028]

Je veux bien le sujet ce serait cool de ta part !
Je connaissais pas ce concours, tu peux m'en dire plus ?

[Elie520]

Coucou, je suis parmi ceux qui l'ont passé aussi !!
Alors moi perso, exo 3 très très dur, pas du tout assez avancé dans le programme, puis pas d'inspi xD
L'exo un résolu de manière purementgéométrique, du coup, g assé galéré, é mon préférééé, L'EXO 2 =D
J'ai trouvé que c'était le plus facile pour ma part, du moins a conjecturer. (Niveau demonstration, 'y ai pas mis grand chose ^^)

Donc Moi voila ce que j'ai trouvé : (je trouve pas les congruences sur ce forum, donc considérons k un entier)
si n=4k, alors t(n)=n
si n=4k+1, alors t(n)=n-1
Si n=4k+2 ou n=4k+3, alors t(n)=n-2

C'est de manière assez intuitive donc dure a expliquer par écrit pour ma part, et surtout peu certain.

Ensuite,
si n=4k, alors u(n)=(3/4)n
si n=4k+1, alors u(n)=(3/4)(n-1)
si n=4k+2, alors u(n)=(3/4)(n-2)
si n=4k+3, alors u(n)=(3/4)(n-3)+1=(3n-5)/4

Voila !! Dites moi pour vous !!

[A voir en vidéo sur Futura]

[invite6c146f6c]

Ben, moi je trouve t(5)=5, quand je fais des figure j'arrive facilement à avoir mes 5 cas possibles, ou alors il y en a deux qui s'équivaut, où un des triangles est déjà utilisé dans une autre configuration...

comment montre-tu que t(5)=4 ??

Sinon, l'éxo 1 j'ai pratiquement tout le temps utilisé thales pour retrouver la formule fondamentale de l'homothétie, par contre j'ai perdu un peu de temps dans la rédaction ...

[invite6c146f6c]

Dsl scemamadan mon scanner n'a pas envie de marcher ce soir, sinon le concours général est une épreuve purement honorifique qui est proposé dans la plupart des matières niveau 1ere et terminal, éventuellement les 18 premiers sont primés (au max), elle permet de voir des choses du programme en beaucoup beaucoup plus approfondi, si tu veux d'autres annales va sur Math-express. Voila

[inviteff4eb309]

Bonsoir,

Ma réponse est un peu différente de celle proposée précédemment...

J'ai mis:
on considère la division euclidienne de n par 4:
n=4q+r
pour r inférieur ou égal à 2, on a t(n)=4q et u(n)=3q
pour r=3, on a t(n) = 4q+1 et u(n)=3q+1

Pour démontrer ça, c'était un peu plus long, je n'ai pas le temps de tout écrire.
Est-ce que quelqu'un d'autre a trouvé ça? Peut on avoir un post avec des figures pour justifier l'autre réponse: je n'ai pas réussi à faire 5 triangles avec 6 points...
Selon mes figures il faut attendre n=7, et donc 3 points de plus pour créer un 5° triangle, à coté de la figure.
Devait on utiliser tout les points sur la figure?

[inviteff4eb309]

Je ne suis pas sur de la réponse de Elie:
prenons n=8
Traçons deux carrés, avec leurs diagonales. Ils n'ont aucun coté en commun.
Sur chaque carré, on a 4 triangles recherchés,(donc 8 au total).
Or,8=4k. et (3*8/4)=6
Donc, le u(n) défini pour 8=4k est (sauf erreur de ma part) faux...
bonne soirée

[Elie520]

Pour te répondre Ares74, je crois ke tu as effectivement fait une erreur si ce n'est moi, parce que la formule que tu dois appliquer dans ton cas est celle pour la fonction t, ou la condition supplémentaire n'est pas prise en compte, et pas la fonction u. Ainsi, on a bien 8=4k, d'ou t(8)=8. Ai-je bien répondu ?

Et sinon, en effet, pour n=5 et n=6 dans le première partie de l'exo, je n'utilise respectivement pas un et deux points, puisqu'on ne peut rien en faire.
En fait, ma réponse est basée sur le fait que le nombre de triangle marche par quatre quand on a quatre points (je parle pour la fonction t).
Ainsi, a chaque fois qu'on a quatre points en plus, on rajoute 4 triangles. d'ou quand n=4k, t(n)=n.
Ensuite, on ne peut rien faire avec seulement un point ou deux en plus. d'ou t(n)=n-1 et t(n)=n-2 pour n=4k+1 et n=4k+2. Enfin, avec trois points en plus, on peut former un unique triangle en plus, ce qui donne aussi t(n)=n-3+1=n-2 si n=4k+3.
Pas évident d'être clair....

[Elie520]

Et pour te répondre Beub, démontrons t(5)=4.
Soient A,B,C,D etED 5 points du plans non alignés 3 à 3.
Voici un exemple de triangles possibles respectant les conditions de la première partie de l'énoncé:

ABC
AB D
BCD
A CD

On n'utilise pas E. En effet, si nous le voulions, il faudrait enlever deux triangles pour qu'ils aient tous soit 2 soit zéro sommet en commun. Donc t(5)=4.
P.S.: Je n'ai pas utilisé E, mais on peut faire pareil pour A, B, C ou D, cela revient au même.

[Elie520]

"[...]A, B, C, D et E[...]" pardon.

[invite55dcb7a8]

Bonsoir,

voila, si certains veulent le sujet demandé je peut le mettre à disposition..

SVP Moi :P

[invite8f458b62]

Coucou les gens, alors j'ai moi aussi passé ce fabuleux concours général.

Pour ma part, j'ai plutôt réussi l'exercice 1, à l'exception de la question 4 et 6 (mais la 6 un ami l'a faite, en utilisant Thalès).

L'exercice 3, aussi surprenant soit-il, je l'ai trouvé abordable... Enfin abordable par rapport à la difficulté de l'ensemble. J'ai fait 1)a et b ; la question 2 j'ai fait la a, la b en admettant an>bn>cn (oui je sais que c'est plus facile comme ça mais bon ) et j'ai vaguement fait le reste (enfin quelques trucs par ci, par là...)

Et l'exo 2... Presque pas touché. Pour moi l'énoncé est fichtrement mal formulé ! "n points tels que 3 quelconques d'entre eux ne soient pas alignés" : comment le comprendre ? Moi j'ai commencé par aborder l'exercice en me disant que ça voulait dire "tous les points alignés sauf 3" mais ça n'avait aucun sens. Ils auraient du mettre "ne soient jamais alignés"...
Quoi qu'il en soit, je suis parvenu à t(4) et un mec (qui avait l'air de s'en être très bien sorti) a réussi à faire t(5) = 5.

Il m'a ensuite vaguement expliqué que la suite t(n) s'exprimait de la sorte :
t(4) = 4
t(5) = 5
t(6) = 5 = t(5) + t(1)
t(7) = 5 = t(5) + t(2)
etc...
autrement dit, pour n = 5q + r ; (q et r le quotient et le reste de la division euclidienne de n par 5)

t(n) = t(5q) + t(k)

(il m'a assuré que ça se démontrait "facilement" avec une récurrence...)

Par contre il n'a pas réussi la 3 et 4.

Bref, je crois que le concours général mérite sa réputation. Ça reste une chouette expérience, et ça permet de relativiser quant à son niveau en mathématiques ^.^

[Elie520]

Tout à fait d'accrd pour la mal-formulation de l'exo qui aurait du etre "3 points ne soient jamais alignés" !

Et je n'arrive pas à trouver t(5)=5... Pourrait-il te préciser pour les points A, B, C, D et E par exemple ?

Et si quelqu'un qui lit se forum est sur des réponses des l'exercice deux, il est largement invité à répondre !!! Je suis curieux de savoir !

Merci.

[invite8f458b62]

Bah mince ! Je suis en train de réaliser que la configuration qu'il m'avait donné ne tiens pas la route

Désolé, je ne peux pas lui demander plus de détails, en fait je ne le connais pas. Je l'avais juste déjà aperçu parce que l'an dernier j'ai reçu un accessit à un concours de maths et il avait obtenu la 3ème place. Et j'ai parlé avec lui à la fin du concours ^.^

Bah ça alors... Ça casse un peu la crédibilité de mon post précédent... >.<

Pfff... Quel exo !

Désolé de ne pas être d'un plus grand secours... Je continue à chercher mais je doute franchement...

[Elie520]

Lol, D'accord =)
Ben moi je suis à peu près persuadé de ma réponse (mais pas à 100%), mais je l'ai balancée comme ca sur la copie... Même pas cherché a justifier donc ca m'embête un peu...

[invite55dcb7a8]

Si vous mettez en ligne vos sujets on pourra ptet vous aider...

[invite8f458b62]

Moi je regrette qu'il n'y ait pas un classement à plus petite échelle. Je sais bien qu'à l'échelle nationale, en ayant fait environ la moitié du truc sérieusement, je n'ai aucune chance.
Mais l'an dernier j'avais fait les Olympiades de mathématiques, et j'avais reçu un accessit à l'échelle de ma "zone" (enfin je sais que ça allait de Avignon à Perpignan), et pourtant j'avais pas forcément tout réussi ^.^

[Elie520]

C'est pas faux Yangous...
Bon ben g preté le sujet a un ami alors je ne l'ai plus, mais si je me souviens bien, voici la première partie de l'énoncé.

On considère dans le plan n points (n>2) tels que trois de ces points choisis au hasard ne soient jamais alignés.
On veut construire des triangles à l'aide de ces points en respectant la condition suivante : "deux triangles quelconques choisis au hasard ont soit deux soit zéro sommets en commun, mais jamais un seul".
On note t(n) le nombre maximal de triangle constructibles dans ces conditions à partir de n points.
Questions :
1) Montrer t(4)=4, et trouver t(5) et t(6).
2) Montrer t(n)<_{ou égal} n, et enfin, exprimer exactement t(n) en fonction de n.

L'énoncé comportait une seconde partie avec une condition supplémentaire sur les triangles, mais pour l'instant, on s'arrete là ^^

Voila Voila !
Bonne chance.

[Elie520]

Ah et au fait Ares74, je n'avais pas remarqué dès le début, mais ta réponse et la mienne sont équivalente ! Nous sommes donc deux à avoir trouvé la même chose =)

[invite8f458b62]

Oui c'est quasiment ça l'énoncé =)
sauf le "trois de ces points au hasard ne soient jamais aligné" ; la phrase exacte c'est "n point tels que trois d'entre eux ne soient pas alignés". Déjà là première ambiguïté ; trois points non aligné "en tout" ?

Ensuite, j'ai pas aimé le "deux triangles choisis au hasard ont 0 ou 2 côtés commun" , les triangles considérés sont uniquement ceux formés à partir des n points ? Ou ceux apparaissant comme étant le fruit d'intersections ces segments formés ?...

(exemple, si on formait un carré avec les 4 points, en reliant les diagonales, on formerait combien de triangles ? 4 ou 8 ?...) Vu la réponse t(4) = 4, on comprend que non, mais ça me semble pas clair...

Bref, un sale énoncé...

[Elie520]

J'avoue, ben moi j'ai compris que les intersections ne formaient pas de triangles, et on a bien confirmation avec t(4)=4. Et pour la phrase des points alignés, je l'ai modifiée pour justement enlever l'ambiguïté héhéhé !

[invite55dcb7a8]

C'est clair qu'il faut prendre en compte uniquement les triangles dont les sommets sont déjà fixés

[invite8f458b62]

Ouais enfin moi j'ai pas procédé comme ça et je vois rien qui me semble infirmer explicitement ma compréhension du truc...
C'est pour ça que j'ai laissé tomber l'exo ><

enfin d'un côté, même en le comprenant, je ne pense pas que je l'aurais réussi ^.^

Mais quand même, c'est rageant

[invite6c146f6c]

Je pense ne pas avoir compris correctement la question de l'éxo 2, car avec 5 points on peut faire 10 triangles différents, 45 possibilité d'avoir 2 triangles distincts et quand on "enlève" les configurations où deux triangles on que 1 sommet en commun, on peut en trouver un paquet....

Est-ce que quelqu'un peut m'expliquer t(n)? comment on le construit ??? combien de triangles on formes pour le calculer, on les dessines tous et on compte combien il y a de fois 2 triangles distincts respectant les conditions initiales? ou on fait autrement???

Personnellement je suis déçu de ce que j'ai fait jeudi, car toutes les annales que j'avais fait (les sujets de 2004 à 2009) celui de 2010 est celui où j'en ai fait le moins.

[Elie520]

En fait, t(n) est les nbr maximum de triangles que tu peux faire, de quelque manière que ce soit. C'est donc pas de la anière dont tu les fait qui compte, mais le nombre que tu peux faire d'un coup au maximum, parce qu'il y a évidemment plusieurs manière d'aboutir à quatre triangles.

[invite95c571c1]

Voilà ma correction de l'exo 2 (si j'ai bien compris l'énoncé) :



D'où t(4) = 4, t(5) = 4, t(6) = 4, t(7) = 5

On peut généraliser comme ça :
Si n = 4 q + r (q et r entiers), alors t(n) = 4 q + t(r)
où t(1) = 0, t(2) = 0, t(3) = 1.

Si quelqu'un a la solution de la question 4 de l'exo 1, je suis preneur = )

[invite95c571c1]

La suite de l'exo 2 part de cette construction (je trouve la même chose alors que Elie en page 1) :

[invite8f458b62]

Ixnay ; ce que tu as fait me semble tout à fait cohérent.

Par contre je ne comprends pas ce que tu entends par "la suite de l'exo commence comme ça" ; tu parles de la question 2 pour laquelle on considère que les triangles n'ont pas le droit de se chevaucher ?

Dans ce cas, si on considère que ta construction est bonne, tu as 4 triangles non ? or on nous dit "u(4) = 3"...

Décidément, je déteste cet exercice.

[invite95c571c1]

Ixnay ; ce que tu as fait me semble tout à fait cohérent.

Par contre je ne comprends pas ce que tu entends par "la suite de l'exo commence comme ça" ; tu parles de la question 2 pour laquelle on considère que les triangles n'ont pas le droit de se chevaucher ?

Dans ce cas, si on considère que ta construction est bonne, tu as 4 triangles non ? or on nous dit "u(4) = 3"...

Décidément, je déteste cet exercice.

Non, ca se voit difficilement mais j'en ai tracé que trois ^^ .