Resolution ex 107 p 47 1ere S

[invitedfa0143e]

Bonjour,
J'ai un exercice Dm sur les fonctions polynômes de second degré a faire: Voici les consignes,
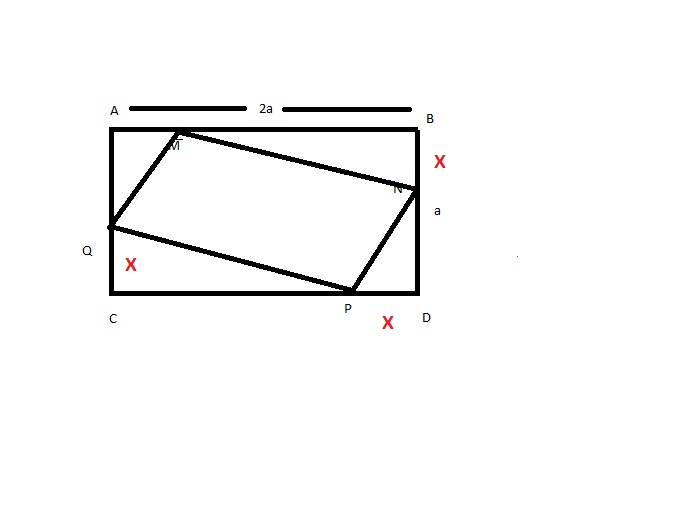
ABCD est un rectangle, de côtés a et 2a (avec a>0). Les points M,N,P et Q appartiennent respectivement aux côtés [AB], [BC], [DC] et [AD].
De plus AM = BN = CP =DQ.

Déterminer la position du point M sur [AB] pour que l'aire du quadrilatère MNPQ soit minimale.


Je sais que M doit être situé au milieu de AB mais je ne sais pas comment le prouver sous forme de fonction polynôme...

Merci d'avance !
-----

[invitedfa0143e]

Désolé c'est l'exercice 107 page 54 et non pas 47

[Kley]

Salut didine25,
Commence par faire un beau dessin, en mettant les valeurs de chaque coté, on dira que AM = BN = CP =DQ=x
Essaye d'exprimer la surface du quadrilatère par rapport à celle du rectangle (en fonction de a et x).

[invitea36b62f2]

Salut didine25,
Commence par faire un beau dessin, en mettant les valeurs de chaque coté, on dira que AM = BN = CP =DQ=x
Essaye d'exprimer la surface du quadrilatère par rapport à celle du rectangle (en fonction de a et x).

pourrait tu donner la correction détaillée, je ne comprend toujours pas.
Merci d'avance

[A voir en vidéo sur Futura]

[Kley]

pourrait tu donner la correction détaillée, je ne comprend toujours pas.
Merci d'avance

Salut,

Quelle est la surface du rectangle ABCD ?
La surface quadrilatére MNPQ n'est elle pas égal à:
La surface du rectangle - celle des 4 triangles,
Je te laisse metre cela en équation, l'exercice est bon!

[invitec5f7e4bb]

Salut,
Pièce jointe 123301
Quelle est la surface du rectangle ABCD ?
La surface quadrilatére MNPQ n'est elle pas égal à:
La surface du rectangle - celle des 4 triangles,
Je te laisse metre cela en équation, l'exercice est bon!

J'ai exactement le même exercice. Donc j'ai calculer l'aire de MNPQ: j'ai trouvé 2a²+x²-3ax+x. Mais après ? Si je pratique la méthode par identification ça me fait: a=2a²+x²; b=-3ax+1; et c=0. Donc Delta=b²-4ac=9a²+1. Donc vu que Delta>0, il a deux solutions:
X1: (-b-racine de delta)/2a=0
X2: (-b+racine de delta)/2a=3/2a+2

J'en suis à là. Mais je crois que je fais fausse piste. Quelqu'un pourrait m'aider ? Merci =).

[invitea2788a8c]

j'ai trouvé 2a²+x²-3ax+x.

Est-tu sûr ? Moi j'ai 2a²+2x²-3ax

[invitec5f7e4bb]

Est-tu sûr ? Moi j'ai 2a²+2x²-3ax

J'ai oublié de revenir posté un message . Effectivement je trouve aussi 2a² + 2x² -3ax

[invitea2788a8c]

Pour la suite ... il faut considérer que c'est une fonction de x et réfléchir à trouver la valeur de x pour laquelle la fonction à un minimum ...

[invitec5f7e4bb]

Donc si j'ai bien compris, Aire de MNPQ = f(x)= 2a² +2x² -3ax avec:
a= 2a² + 2x²;
b=-3ax
et c=0.
Donc c'est une fonction trinôme. Donc à partir de là, le minimum est :
-delta/4a atteint pour -b/2a.

C'est bien ça ?

[invitea2788a8c]

Aire de MNPQ = f(x)= 2a² +2x² -3ax --> OK

Dans cette fonction la valeur de a est une constante, c'est une caractéristique du rectangle dans lequel on a décrit le problème. Quelque soit la valeur de a , ma solution sera la même.

On a donc un fonction polynome de degré 2 de la forme Ax²+Bx+C avec :
A=2
B= 3a
C= 2a²

La représentation graphique de cette fonction est une parabole (comme toutes les fonctions de cette forme) passant par un minimum ( car A est positif ) .

--> il faut trouver la valeur de ce minimum ...

[invitec5f7e4bb]

Ah d'accord, mais dans ce cas là, je mettrais plutot:

A= 2
B= -3a
C= 2a²

Donc delta= b²-4ac = (-3a)² + 4*2*2a² = 9a² + 16a² = 25a²

Donc le minimum est -delta/4a atteint pour -b/2a.

Donc-delta/4a = (-25a²)/(4*2) = (-25a²)/8

Et -b/2a = -(-3a)/2*2 = 3a/4

Donc le minimum est (-25a²)/8 atteint pour 3a/4 ?

[invitec5f7e4bb]

Ah d'accord, mais dans ce cas là, je mettrais plutot:

A= 2
B= -3a
C= 2a²

Donc delta= b²-4ac = (-3a)² + 4*2*2a² = 9a² + 16a² = 25a²

Donc le minimum est -delta/4a atteint pour -b/2a.

Donc-delta/4a = (-25a²)/(4*2) = (-25a²)/8

Et -b/2a = -(-3a)/2*2 = 3a/4

Donc le minimum est (-25a²)/8 atteint pour 3a/4 ?

Petite erreur =S. Delta = b² - 4ac = (-3a)² - 4*2*2a² = 9a² - 16a² = -7a²

[invitea2788a8c]

Au temps pour moi B = -3a .
Delta = -7a² et le minimum est atteint pour x= -B / 2A ..

Il y avait une autre façon d'arriver au résultat en considérant que dans ce cas le minimum de la fonction est atteint lorsque la dérivée de la fonction est égal à 0 .

La dérivée de f(x)= 2a² +2x² -3ax étant f '(x)= 4x-3a
f ' (x) =0 <=> 4x-3a=0 <=> x = 3a/4

[invitec5f7e4bb]

Je n'aurais pas trouvé avec cette façon =S Je n'ai toujours pas appris les dérivées .
Résultat je ne comprend pas bien ton dernier paragraphe =S, désolé . Mais je te remercie pour m'avoir aidé, je n'aurais pas trouvé le A, B et C. Merci encore