Bonjour,
je me suis récemment penché sur un exercice de spé maths sur les similitudes planes qui m'a posé un doute.
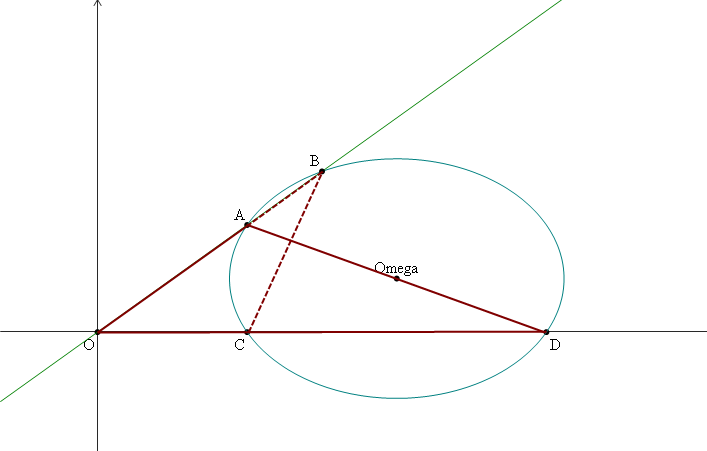
Dans l'exercice, on considérait une similitude non directe S qui transformait un triangle OCB en un triangle OAD.
Les questions étaient: 1) Montrer que S est une similitude non directe qui transforme le triangle OCB en le triangle OAD différente d'une symétrie axiale puis 2) Déterminer un point fixe de S et montrer que c'est le seul.
Ce sont les questions en gras qui me posent problème.
En effet, comme on le dit souvent, cela ne veut pas dire que le point O est transformé en O, le point C en A et le point B en D. Ainsi, le point O pourrait très bien être transformé en A.
Mais on avait auparavant démontré que ces 2 triangles étaient semblables: l'angle BOC= l'angle AOD, l'angle OAD=l'angleOCB, l'angle OBC=l'angle ADO (on pourrait même évoquer de égalités d'angle orientés, mais ce serait plus laborieux)
Cela suffit-il pour affirmer que OA/OC=OD/OB=AD/CB?
En supposant que l'affirmation est correcte, peut-on alors dire en nous servant de cette égalité de rapport que S(O)=O, S(B)=D et S(C)=A ?
Si oui, alors on peut considérer que O est le centre de S, et que comme (OB,OC)=-(OD,OA), que S est une similitude indirecte?
Mais dans ce cas, l'ordre des questions n'est plus respecté...
Si on voulait le suivre, il faudrait d'abord déterminer 2 angles opposés, tel que (OB,OC)=-(OD,OA), mais comment faire, si on ne sait pas quel point est transformé en quel point, car on pourrait tout aussi bien dire: (OB,OC)=(OA,OD)....
-----