Points sur la même ligne.

[invite65b24cec]

Bonjour !

Je coince sur un problème que mon prof nous a donné.
Nous sommes principalement en train de voir les vecteurs, donc le problème devrait se résoudre avec leur aide.

Voici le problème (j'ai mis des notes supplémentaires en vert)

Soit A,B,C et A,D,E sont sur la même ligne (donc une ligne ABC et une ligne ADE)
Soit F le point d'intersection de [BE] et [CD]
Soit P le point médian de [AF] (pas sûr du terme exact, le cours étant en anglais, c'est le point qui coupe le segment en deux)
Soit Q le point médian de [BD]
Soit R le point médian de [CE]

Montrez que P,Q,R sont sur la même ligne


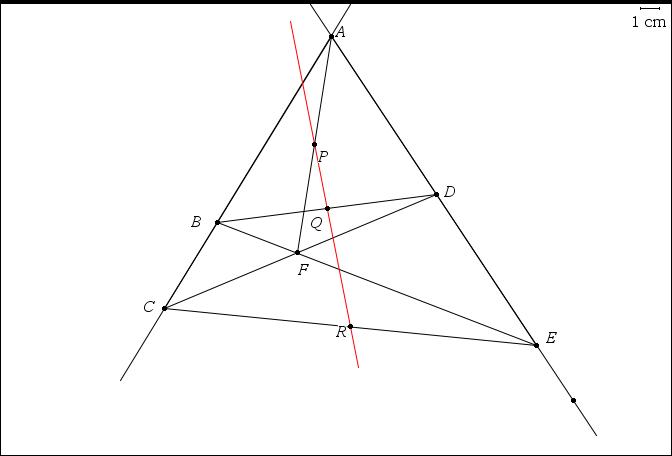
Voilà le problème, et ici une représentation graphique du problème.

J'ai déjà déduit qu'un des moyens de prouver que P,Q,R sont sur la même ligne, il suffisait de prouver que les vecteurs PQ et PR sont parallèles et donc que leur déterminant est égal à zéro (det(PQ,PR) = 0). Le problème est qu'aucune donnée sur les coordonées des points ou sur les angles n'est fournie, j'ai donc essayé de calculer en donnant des coordonées aux points (par exemple P(,);Q(,)) et en utilisant le fait qu'ils soient tous des points médians.
Petit extrait : det(PQ,PR) = det(OQ-OP,OR-OP) = det


etc.
Mais je suis toujours coincé, en fait, je ne sais pas vraiment dans quelle direction aller.

Merci d'avance !
-----

[invitec8e03ff9]

on peut prendre (A,C ,E) comme repère alors A(0,0) ;C(1,0),E(0,1);B(b,0);D(0,d),Q (b/2,d/2),R(1/2,1/2) et vérifier que F((b(1-d)/(1-bd);(d-1)/(1-bd)) avec comme vous le voyer b<1 ; d<1 calculer les composantes des deux vecteurs PQ et QR a vous de completer et de demontrer que les points P;Q et R sont alignées

[invitec8e03ff9]

je m'excuse vérifier que F(b(1-d)/(1-bd); d(1-b)/(1-bd) ) donc P ( b(1-d)/2(1-bd) ; d(1-b)/2(1-bd) ) on est sure que 1-bd non nul car b<1 et d<1

[invite65b24cec]

ça a marché comme ça !
Merci beaucoup !

[A voir en vidéo sur Futura]

[invitec8e03ff9]

oui pas de quoi