Probléme géométrie

[invite02c2ba1c]

Bonjour !

Quelqu'un saurais-t-il m'aider pour cet exercice ...
J'arrive a trouver la fonction mais je ne vois pas comment répondre aux questions ...

Sujet :
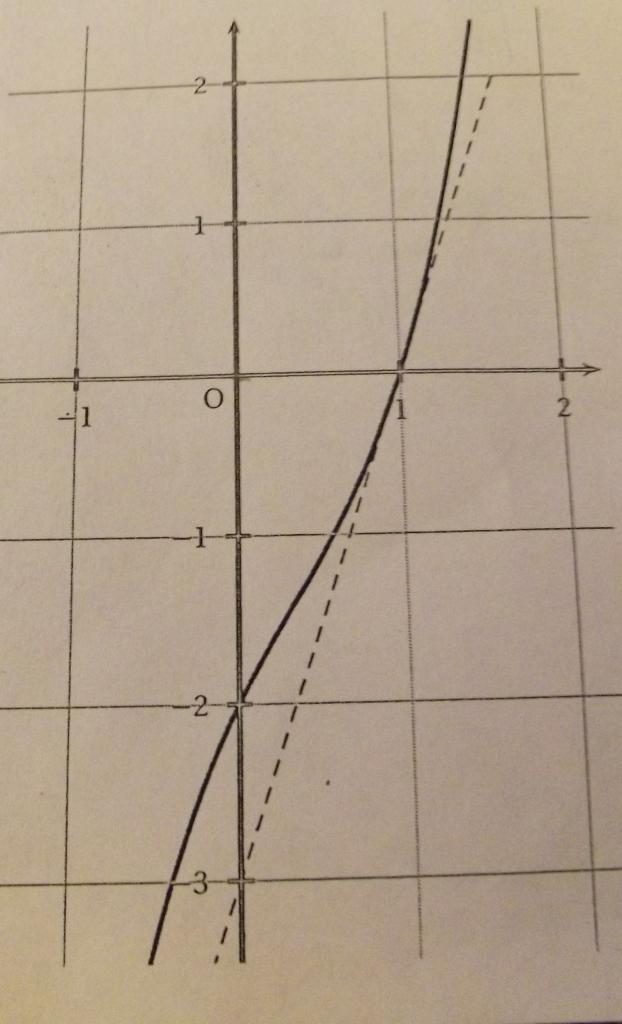
La courbe ci-contre est la représentation graphique d'une fonction g définie sur R par :
g(x) = x^3 - x^2 +ax+b
ou a et b désignent deux nombres réels.
On suppose g strictement croissante sur R.
Cette courbe coupe les axes de coordonnées aux points A(1;0) et B(0;-2).
La droite en pointillés est la tangente à la courbe au point d'abscisses 1. Elle coupe l'axe des ordonnées au point C(0;-3)

1°) Lire g(1)
En déduire une relation entre a et b
2°) Donner la valeur de g'(1)
Ecrire alors une relation vérifiée par a
3°) A l'aide des deux premières questions déterminer les valeurs de a et b.
4°) Donner le signe de g(x) sur R

Courbe :


1°) g(1) = 0
Relation entre a et b ????

2°) g'(1)= ??
Relation ???
3°) a= 2 et b= -2
Mais je ne l'ai pas fait avec les deux premières questions ...

4°) ???

Voila, en clair, je n'arrive a rien, si quelqu'un aurais la gentillesse de me donner une petite piste ...
Merci d'avance !
-----

[zyket]

1°) g(1) = 0

dans l'expression

g(x) = x^3 - x^2 +ax+b

tu remplaces x par 1 , tu obtiens donc une égalité du type g(1)=1^3 ....etc qui finalement aboutit à g(1)=(quelque chose en fonction de a et b)

Or comme tu l'as vu sur la représentation graphique (et aussi d'après le fait que A(1;0) est sur la courbe représentative de g) g(1) = 0 d'où le (quelque chose en fonction de a et b)=0

[pallas]

tu vois que g(1) = 0 donc tu remplaces x par 1 et tu obtiens une premiere relation entre a et b à savoir 0=1^3-1²+ax1+b !!
de même tu calcule g'(x)= 3x² +......... ( atoi )
tu les sur la courbe que la pente de la tangent en 1 est g'(1) = 3 ( delta y/delta x) doc dans g'(x) tu remplace par x ....