Recherche d'une formule?!

[invitee1987b04]

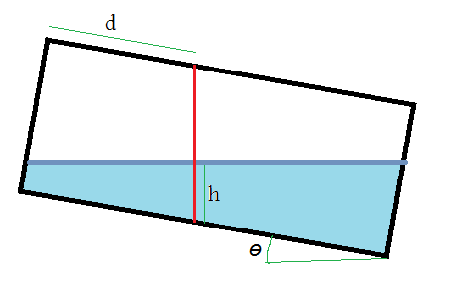
Bonjour à tous, voila j'ai un problème et on me demande de le résoudre, j'aimerais simplement en savoir la formule.
Voila l'énoncé: Je dispose d'une citerne à mazout de 1200L placée horizontalement faisant 1m50 de long et 1m de haut, je ne possède pas de jauge, je peux seulement mesurer le niveau de mazout qu'il me reste avec une corde.
Quand je remonte la corde, 53 cm de la corde de longeur 1m sont mouillés.
1)Comment savoir le nombre de litres qu'il me reste dans ma cuve?
2) Si j'incline la cuve de 10°, combien reste-t-il de litres?
Je le répète, j'ai seulement besoin de la formule!!

Merci de votre aide
-----

[invitee4135479]

d'abord il faut précisé si c'est la citerne est cylindrique ou pas?
le volume d'un cylindre est V=TTr²h ou r est le rayon du disque de la base du cylindre et h la hauteur du cylindre .

[invitee1987b04]

La citerne est bien cylindrique!!

[invitee4135479]

V=TTr²h=1200 avec h=1,5m et r= 0.5m.

le niveau de mazout dans la citerne est 0.53m. ==> la citerne est rempli a 53% du volume total.

donc 53% de 1200 est 53*1200/100=53*12=636L. donc il reste 636L de mazout dans la citerne.

[A voir en vidéo sur Futura]

[ansset]

V=TTr²h=1200 avec h=1,5m et r= 0.5m.

le niveau de mazout dans la citerne est 0.53m. ==> la citerne est rempli a 53% du volume total.

donc 53% de 1200 est 53*1200/100=53*12=636L. donc il reste 636L de mazout dans la citerne.

non, le volume de mazout n'est pas proportionnel au niveau ( jutement parcequ'elle est cylindrique )

[invitee4135479]

oui c'est vrai, j'ai la tête dans la neige.c'est pas du tout proportionnel a cause de la forme cylindrique.

[Tryss]

non, le volume de mazout n'est pas proportionnel au niveau ( jutement parcequ'elle est cylindrique )

Tout dépend dans quel sens est posé le cylindre

Dans ce qui va suivre, je me place dans le cas ou la cuve vue de coté ressemble à un cercle

Pour le volume "a plat" ça peut se faire assez simplement avec de la trigonométrie, l'aire d'un triangle et d'un cercle

En notant h la longueur mouillée, on trouve :



Pour la question 2, tout dépend du point de mesure, et il n'y à plus de solution géométrique simple.

Si le point de mesure a une distance du bord le plus haut de la cuve, que l'on mesure une longueur mouillée et qu'elle est penchée d'un angle , le volume est alors donné par l'intégrale suivante :



Il existe une expression "simple" de cette intégrale, mais elle est assez longue, donc je la découpe :






A noter qu'il est possible que des erreurs se soient glissés dans cette dernière formule

Edit : attention, ceci est faux, j'ai pas mis l'angle droit au bon endroit -_-'

[ansset]

bonjour tryss.
je suppose qu'elle est "à plat" comme une cuve ( d'ailleurs il est précisé horizontalement )
mais je ne trouve pas le même volume que toi.
en fait , pour moi h est la longueur de la cuve
et si R est son rayon, le volume total ( plein ) est bien h*pi*R²
donc le volume de mazout à l'interieur vaut :
h*pi*(quelquechose ) en fonction du taux de remplissage.
donc je ne comprend pas ce que tu appelles longueur mouillée, ni pourquoi h se retrouve sous l'arcsin !

en supposant en premier calcul qu'elle soit remplie à moins de la moitie.
( l'autre cas se deduisant du premier )
si x est la hauteur de fuel donc je prend a=R-x
je trouve
V=h*R²(arcos(a/R)-0,5sin(2arcos(a/R))
soit si
theta =arcos(a/R) ( angle de la hauteur de fuel au bord par rapport au centre )
V=h*R²(theta-0,5sin(2*theta))

[invitee4135479]

déja les dimension donnée et le volume total du citerne sont incompatible/
V=TTr²h=TT(0.5)²(1.5)=1.178m^3 =1178L. bon c'est presque 1200L.
la citerne est bien posé horizontalement,donc y a pas de proportionnalité entre l volume et la hauteur.si la citerne été posé verticalement ca serait bien proportionnel.
la citerne est rempli un peu plus que la moitie.

[Tryss]

La longueur mouillée est la longueur mouillée du fil qui a servi à faire la mesure, pas la longueur de la cuve.(mon h=le x de ansset)

Si la cuve est pleine h=1, si la cuve est à moitié pleine h=0.5 et si la cuve est vide h=0

Sinon ansset tu trouves bien le même volume que moi, juste écrit différemment

(par contre la version inclinée est une horreur

[Duke Alchemist]

Bonjour.

(par contre la version inclinée est une horreur

Pour moi, c'est pas parce qu'on incline la cuve que le volume de liquide contenu dans la cuve va changer...

Quoi ? J'ai dit une bêtise ?...

Duke.

[ansset]

là on s'emmelle tous dans les variables, qu'on appelle pas de la même manière.
pour moi, elle est alongée donc un cylindre posé.
la hauteur totale de l'énoncé est donc pour moi le diamètre du cylindre.
et sa longueur est h tel que dis dans l'enoncé.
sinon:
@Aziza:
le fait qu'elle soit plus qu'à demi pleine ne change pas le principe du calcul.
on a une moitié remplie soit h*pi*R²/2 plus qcq chose.
le qcq chose se calcule de manière équivalente au calcul initial. ( même principe )
sauf qu'on calcule le fuel en plus et pas le vide en plus.
@Tryss :
oui effectivement si ton h est mon x , tout va bien , on retombe sur nos papattes
on peut ecrire l'équation de plusieures manières

cordialement

quand au modèle incliné, tu as raison, et je suis en panne de doliprane
d'ailleurs, comme dit Duke je ne visualise ps une version inclinée ni ce qu'on mesure.

[Tryss]

Pour la version inclinée, voila ce que j'ai compris et mes variables :



Sachant que mon intégrale plus haut est dans un cas un peu favorable, il faudrait en fait faire 3 parties pour le cas général : celle ou il n'y a pas de fuel au fond de la cuve, celle ou il y en a mais pas au plafond, et celle ou l'intégralité du volume est rempli

[ansset]

en tant qu'exercice de lycée, je ferais l'hypothèse suivante.
la corde ( ou jauge ) est à un bout ou à un autre de la cuve.
si la cuve est légèrement incliné, alors la profondeur mesurée ( 53 cm ) est simplement surestimée ou sousestimée par rapport à la moyenne dans la cuve.
on peut même faire le calcul ( l'équation affine ) en fonction de la position de la corde le long de la cuve.
du point le plus bas au point le plus haut.
il suffit donc d'estimer la valeur au centre à partir d'une valeur excentrée!
en supposant quand même que la corde est "centrée" par rapport au cercle , donc passe par l'axe de la cuve.

c'est plus simple non ? tryss ?

[Tryss]

Sauf qu'une cuve inclinée à 10° qui a une hauteur de 53cm au milieu n'a pas le même volume de fuel que la même cuve à plat avec 53cm de fuel

Après effectivement, si la cuve est à peu près remplie à la moitié et que l'inclinaison est faible c'est grossièrement égal

[ansset]

non, j'ai dis une bétise la fonction n'est pas affine.
donc je resimplifie avec une mesure au centre pile de la cuve, et il faut effectivement intégrer.
je repart de ma formule
V=h(longueur)*R²(arcos(a/R)-0,5sin(2arcos(a/R))

a étant (pour moi l'ecart entre le milieu de la cuve ( 0,5 ) et la hauteur du fuel , avec
a positif si fuel plus bas que milieu de cuve et a négatif si fuel plus haut .

si la cuve est incliné et la mesure "a" au milieu de la cuve ce coup si alors
a(l)=a+(l-0,75)*tg(10°) et l une position par raport à l'extrémité la plus basse

il faut intégrer le volume entre l=0 et l=1,5 .
soit de R²(arcos(a(l)/R)-0,5sin(2arcos(a(l)/R))dl

puis chang de variable avec théta = arcos(a/R)
et puis j'ai la flemme à l'instant et en panne de clopes.....
a tout biientôt