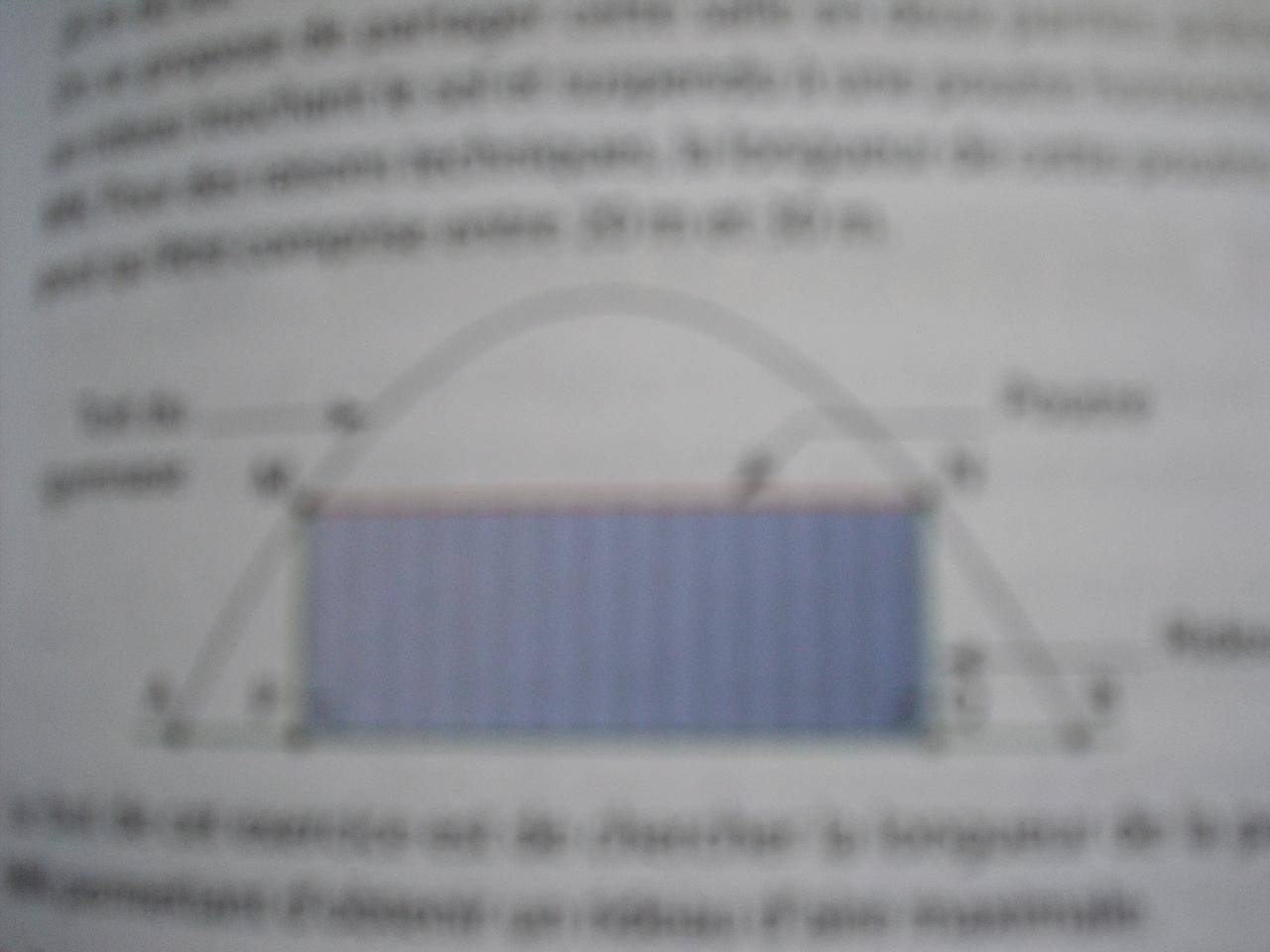
La toiture d'une salle de sport entièrement couverte a pour section transversale une arche de parabole dont 'l'axe vertical passe par le centre de la salle. Les points d'ancrage au sol A et B de cette arche son distants de 40m. Le sommet S de celle-ci est situé à 20m du sol
On se propose de partager la salle en deux parties par un rideau de toile vertical MNPQ touchant le sol et suspendu à une poutre horizontale MN. Pour des raisons pratiques, la longueur de la poutre MN est comprise entre deux valeurs extrêmes : 20m et 30m. L'objectif du problème est de déterminer les dimensions du rideau le plus large possible, sachant que le service des sport peut acheter avec son budget une surface donnée de tissu*
Questions :
1. Dans une repère orthonormal, on considère la parabole P ayant pour sommet S(0,20) et passant part les points A(-20,0) et B(20,0). Montrer que P a pour équation: Y= -1/20x²+20
Réussi.
Les Deux autres questions me pose problèmes les voici.
2. On considere les points M et N de P ayant pour abscisse -x et x avec un reel x appartenant a (10;15). On appelle P et Q les projetés orthogonaux de M et N sur l'axe des abscisses.
a. Exprimer l'aire du rectangle MNOP en fonction de x.
b. Déterminer la valeur de x qui permet que l'aire du rectangle MNOP soit maximale.
3. Déduire des questions précédentes une valeur approchées en mètre, au centimètre pres, de la longueur de la poutre permettant que l'aire du rideau soit maximale.
-----