Bonsoir! Je suis en seconde et j'ai un petit problème de dm: j'ai besoin d'aide!
Voici l'énoncé:
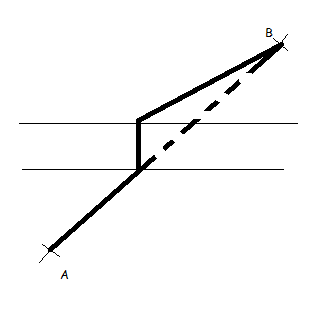
Pour rejoindre 2 villes A et B séparées par une rivière aux bords parallèles, large de 40m, on cherche à construire une route avec les contraintes suivantes:
-le pont doit être le plus court possible
-pour cette largeur de pont, la route doit être la plus courte possible
Conjecturer la position du pont.
Démontrer cette conjecture
B
______________________________ _
rivière
______________________________ _
A
Voilà, merci pour vos réponses.
-----




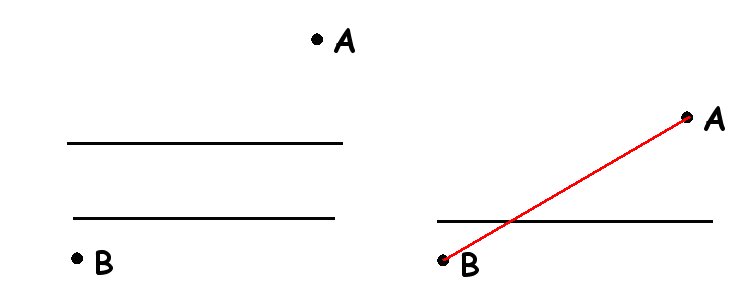
 , il suffirait de joindre A et B par un segment.
, il suffirait de joindre A et B par un segment.





 ou
ou 