Tracé d'une courbe à partir de coordonnées polaires dont le centre est VARIABLE

[invite092c8ad3]

Bonjour à tous,
Je m'intéresse au domaine de l'horlogerie.
L'objectif est de tracer la forme d'un ressort de barillet de montre à partir de 3 équations qui donnent sa forme libre (note: ces équations sont déterminées pour donner une force constante maximale entre le moment ou il est totalement armé, et le moment ou il est désarmé):
equation.png
Avec,
i = numéro de portion de la lame
Li = longueur du ressort armée (donc enroulé dans le barillet) = 2xPIx(rb+(i-1)e)
rb = le rayon d'enroulement initial = constante
e = l'épaisseur de la lame du ressort = constante

On calcule PhiOi et rOi qui sont les coordonnées polaires de la forme du ressort déroulé qui ressemble à ça:
forme ressort.png

Pour tracer cette forme dans des origines cartésiennes, on passe en coordonnées cartésiennes:
Xi= XOi +rOi x cos(PhiOi)
Yi= YOi+ rOi x sin(PhiOi)
Avec Oi= centre du rayon de courbure de la portion de lame i = (XOi,YOi)
Puis on met tout ça dans une table excel et en avant...

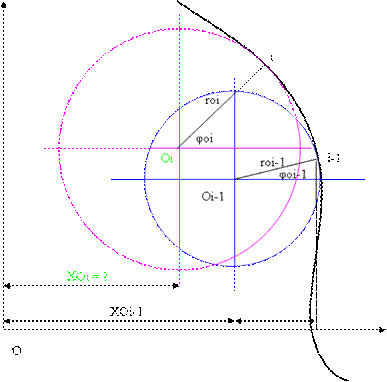
Le hic c'est que le centre Oi de coordonnées polaire n'est pas fixe, il change à chaque incrément de i

Centre variable.png

Je me disais que je pouvais calculer le point Oi à partir de Oi-1 de la façon suivante:
XOi = XOi-1 - rOi-1 x cos (PhiOi-1) + rOi x cos (PhiOi)
YOi = YOi-1 - rOi-1 x sin (PhiOi-1) + rOi x sin (PhiOi)
Mais en fait ça ne me donne pas la bonne courbe et je ne comprends pas pourquoi

L'auteur du livre que je lis semble avoir calculer les coordonnées de Oi de la façon suivante
XOi = XOi-1 - rOi-1 x cos (PhiOi-1) + rOi x cos (PhiOi-1)
XOi = XOi-1 - rOi-1 x sin (PhiOi-1) + rOi x sin (PhiOi-1)
En traçant la courbe ça marche, mais je ne comprends pas du tout sa logique.

J'en appelle à vos talents de mathématiciens car je bloque !
-----

[Médiat]

Bonjour,

Votre courbe ressemble à une clothoïde, en est-ce vraiment une ou est-ce une simple ressemblance ?

[invite092c8ad3]

Bonjour,

Effectivement, je ne connaissais pas cette courbe et après quelques recherches sur internet, je confirme la ressemblance.
Sauf qu'elle est paramétrée toujours par rapport à la même origine, il n'y donc pas de complications au tracé de cette courbe.

Dans mon cas, l'origine change à chaque itération et c'est ce positionnement cartésien variable de l'origine du rayon de courbure que je ne parviens pas à calculer pour pouvoir au final tracer la forme du ressort libre.

[invite092c8ad3]

Cette courbe permet de comprendre un peu mieux ma question:
Il aut partir du principe que seul Xoi est inconnue, puisque Xoi-1 a été calculée précédement.

[A voir en vidéo sur Futura]