arg(1+i) ? je ne comprends pas :(
Bonjour a tous , voila
je ne comprends pas du tout cette reponse dans une correction :
question : Déterminer une mesure de l'angle (AC,AB) (avec des flèches bien sure)
avec a=2 , b=3+i , c=2i
voici la réponse que je n'ai pas compris:
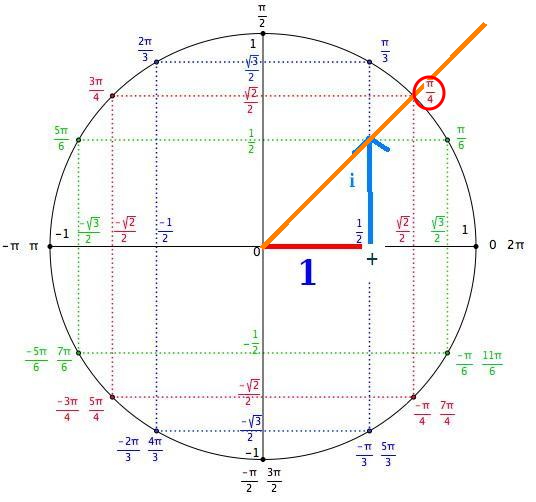
Pourquoi : : 'comme arg(1+i)=PI/4" ???
merci
salut,
arg(a+ib)=arctan(b/a)
tu retrouve cette formule en appliquant le théorème de Pythagore lorsque tu traces a+ib dans le plan complexe.
arg(1+i)=arctan(1/1)=pi/4
sinon si tu traces 1+i dans le plan complexe tu vois que l'angle représente bien 1/4 de l'angle plat (pi)
je n'ai pas tres bien compris malheureusement
car regarde , es c que tu arrive a comprendre le dessin rapide que j'ai fait ? :
j'ai tracer 1+i , j'arrive sur PI/6 et non PI/4 , es normal?
merci de vos réponses d'avance
Bonjour
C'est une erreur d'interprétation du graphe.
C'est un angle qu'on doit lire, et pas une ordonnée sur l'axe :
je t'ai modifié ton image
euh dommage !!
je peut lire aucune pièce jointes
solution?Message vBulletin
Pièce jointe spécifié(e) non valide. Si vous suivez un lien valide, veuillez notifier l'administrateur
il faut attendre que les modérateurs valide l'image
ok , attendons ^^
il était difficile de publier sa via Imageshack? (je vais pas tarder a partir
Imageshack est un site extérieur, étranger, et hors de contrôle (c'est une source de virus notoire). La politique du forum, c'est d'héberger dans la mesure du possible (lorsque des questions légales ne s'y opposent pas) tous les éléments des discussions.Envoyé par Kinano
Ensuite on est sur un forum, pas sur un chat. Ce n'est donc pas l'outil à utiliser dans les cas d'urgence.
Enfin, je t'ai indiqué que tu faisais une erreur de lecture du graphe. C'est bien π/4 qu'on lit comme résultat pour le vecteur 1+i que tu as tracé.
Bah nan , j'ai pas compris
moi je vois : PI/6
comment vous faites ?
C'est l'argument qu'on lit, c'est-à-dire l'angle entre l'axe horizontal et le vecteur.
Pour lire la valeur d'un angle sur ce type de graphe, on trace une droite passant par l'origine et par le point du plan complexe auquel on s'intéresse, et on la prolonge jusqu'au cercle extérieur. La valeur de l'angle se lit à l'intersection entre cette droite et le cercle.
Dans le cas de 1+i , la droite coupe le cercle à la graduation π/4.
Le point (1,0) sur ton cercle, c'est en fait celui où à côté c'est écrit " 0" (tout à droite) De même le point (0,1) c'est celui où à côté c'est écrit "1" (tout en haut). Donc le point (1,1) qui correspond à 1+i se trouve enfait hors du cercle, tout en haut à droite !
Ah tiens, c'est vrai. Je n'avais pas fait attention à l'échelle des axes. Mais cette erreur ne change rien pour ce qui concerne la détermination de l'argument.
@Kinano
En effet tu as tracé le chemin pour aller au point d'affixe z=1/2 +1/2 i. Ce point que l'on va noter M forme avec le point origine O(0;0) un vecteur OM. Vois-tu que l'angle entre le vecteur unitaire de l'axe des abscisses (que l'on note généralement u (avec une flèche)) et ce vecteur OM vaut Pi/4 (45°) ? Or l'argument d'un nombre complexe qui a pour image un point M, c'est l'angle entre le vecteur unitaire de l'axe des abscisses et le vecteur OM. Donc ici arg(1/2 +1/2 i)=Pi/4
Au passage, ce nombre complexe z=1/2 +1/2 i, a le même argument que le nombre complexe z'=1+i que tu cherchais. En effet le point M', image du nombre complexe z'=1+i est sur la demi-droite [OM) , donc l'angle(u;OM')=l'angle(u;OM)=P i/4
D'où arg(1+i)=Pi/4
Dernière modification par zyket ; 05/07/2012 à 22h18.
Mon post précédent proposait une explication géométrique de la chose (il faut souvent avoir à l'esprit l'aspect géométrique des nombres complexes)
On peut aussi démontrer de façon algébrique que arg(1+i)=Pi/4
Pour cela on cherche à écrire le nombre complexe sous forme trigonométrique. C'est à dire z=|z|(cos(têta)+i sin(têta))
La première chose à faire c'est de trouver le module de z=1+i
On a |1+i|=racine de (1²+1²)=racine de 2. Donc |z|=racine de 2
On met le module en facteur dans l'écriture algébrique de z.
On a z=(racine de 2)(1/(racine de 2) + i x 1/(racine de 2))
Quel est l'angle qui a 1/(racine de 2) pour cosinus et 1/(racine de 2) pour sinus ? C'est l'angle Pi/4 (cf le cercle trigonométrique)
Donc z=1+i s'écrit sous forme trigonométrique de la façon suivante : z=(racine de 2)(cos(Pi/4) + i x sin(Pi/4))
D'où arg(1+i)=Pi/4
