Fonction du type Un=f(n)

[invite9740a1da]

Bonjour,
je sèche sur un exercice donné... et j'ai donc besoin de votre d'aide.
Voici l'énoncé:

PARTIE A/

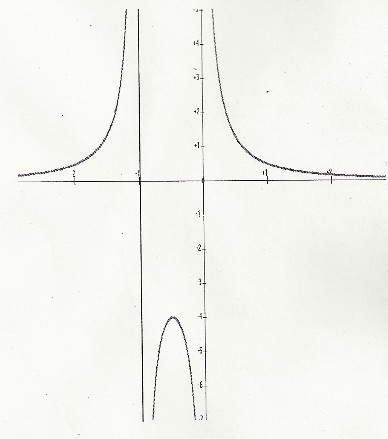
f est la fonction définie sur : D=]-∞;-1[U]-1;0[U]0;+∞[ , représenté ci dessous.


a/ Dresser le tableau de variation de f. On a f(-0.5)=-4 f(1)=1/2 et f(-2)=1/2

J'ai donc fait un tableau de variation:
---------------------------------------------
| X | -∞ -2 -1 -0.5 0 1 +∞ |
---------------------------------------------
|f(x) | / 1/2 / || / -4 \ || \1/2 \ |
---------------------------------------------

Donc jusqu'ici je pense que sa va...

b/ Préciser le signe de f(x) pour X appartenant à D

On peut préciser le signe de f(x) en faisant un tableau de signe; pour xD:

---------------------------------------------------
| X |-∞ -1 0 +∞ |
---------------------------------------------------
| x | - || - || + |
---------------------------------------------------
| x+1 | - || + || + |
---------------------------------------------------
| x(x+1) | + || - || + |
---------------------------------------------------
0 0

C'EST A PARTIR DE LA QUE JE N'ARRIVE PAS:

c/ Préciser le signe de f'(x) pour x appartenant à D.
d/ Résoudre graphiquement f(x) infé ou égal à 1/2.

PARTIE B:

On admet que f(x)= 1/((x+1)x)
a/ Démontrer qu'il existe 2 réels a et b tel que pour tout x de D, f(x)= (a/x)+(b/(x+1)).
b/ u est la suite u_n= f(n). n sup ou égal à 1.
c/ Que deviens u_n quand n devient très grand ?
d/ on pose s_n= u₁+u₂+...+u_n. Montrer que s_n=n/(n+1)et donner la limite de la suite (s_n) quand n tend vers l'infini.

J'espère que quelqu'un pourra m'aider.
Merci =)
-----

[invite9740a1da]

Réponse a la question a/

fff.jpg

réponse a la question b/

tabl.jpg

[invite9740a1da]

Bon j'ai réussi a faire la question c/ et d/ de la partie A. La fonction dérivée de f(x) est supérieur à 0 de -inf a -0.5 ; égale a 0 pour -0.5 ; et inférieur a 0 pour -0.5 a + inf. Et pour F(x) inf ou égale a 1/2, il suffis de tracé y=1/2 graphiquement ce qui donne sur ]-inf;-2]U[1;+inf[.
Si je me suis trompé dite le moi =)

Enfin c'est la que je bloque toujours et encore ! A la partie B !Donc si quelqu'un pourrai m'aider ?!?
Merci

[youtue]

Slt,

Pour la a) de la partie B il te suffit de trafiquer ton expression f(x) pour arriver au resultat attendu
Je ne vois pas ou est la question pour la b).
Lorsque n devient tres grand reviens a dire si dans l'expression de Un (a savoir f(n)) si t'augmentes n est-ce que Un croit ou decroit?
Pour la d) il faut calculer la somme d'une suite puis calculer sa limite (a toi de deviner si c'est une suite geometrique ou arithmetique...

Cordialement

[A voir en vidéo sur Futura]