Droites et plans de l'espace

[Perfectina]

Bonjour,

J'ai un exercice de géométrie dans l'espace auquel je n'arrive pas à répondre.

En voici donc l'énoncé :

Soit ABCD un tétraèdre et M, N et P trois points.
Dans chacun des deux cas suivants, reproduire fidèlement la figure ci-contre et construire la section du tétraèdre ABCD par le plan (MNP).

1) M et N appartiennent au plan (ABC) et P appartient au plan (ABD)

2) M, N et P appartiennent respectivement aux plans (ABD), (ABC) et (ACD)

Remarque 1 :
Par construire on entend justifier, si on construit un point par l'intersection de deux droites, on doit d'abord démontrer que les droites sont sécantes. Si une droite se construit par l'intersection de deux plans on doit démontrer qu'ils sont sécants.

Remarque 2 :
La section cherchée est un polygone dont on doit construire les sommets.

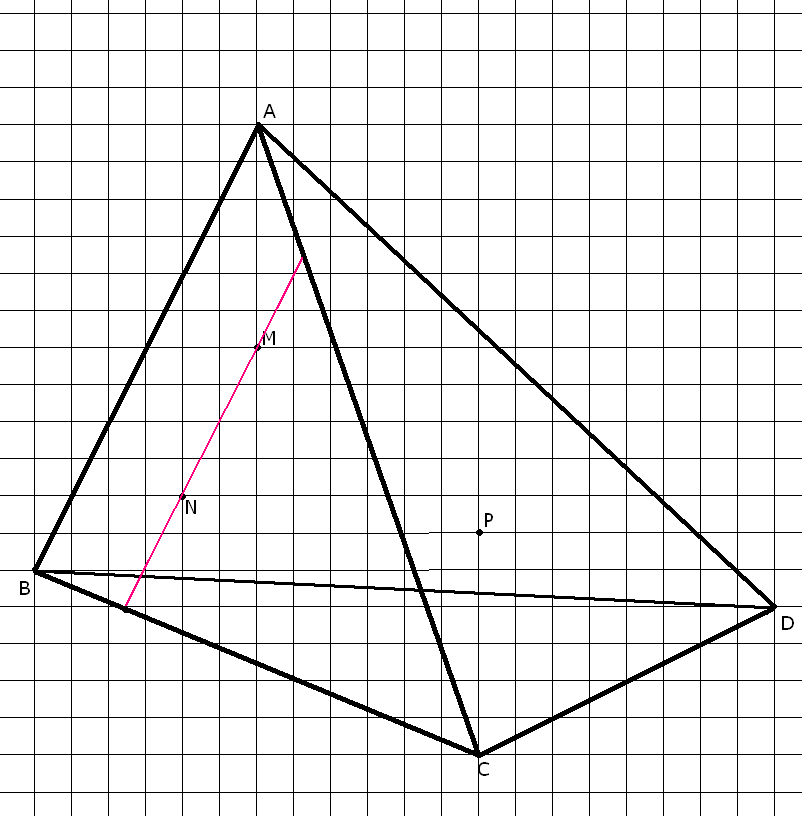
Pour la 1), voilà la figure que j'ai réalisée pour le moment.


Explications :
(MNP) et (ABC) se coupent en la droite (MN) incluse dans (ABC). La tracer donne des points d'intersection coupant (AC) et (BC).

Seulement, je ne sais pas comment continuer. Etant donné que (AB) et (MN) sont potentiellement parallèles, je ne peux pas les faire intersecter.

Merci de bien vouloir m'aider.
Bonne journée à tous !
-----

[sammy93]

Bonsoir.
Pourquoi (MN) serait parallèle à (AB) ? On ne le dit pas dans l'énoncé.Tu peux choisir M et N quelconques.
Il faut surtout JUSTIFIER ce que tu avances.Par exemple:
quand tu dis que (MNP) et (ABC) se coupent selon (MN) et c'est vrai,il faut dire pourquoi.Dans notre cas ,c'est facile car M et N appartiennent respectivement à (MNP) et (ABC) par hypothèse.
Tu détermines l'intersection de (MNP) et (ABD).Il te suffit de prolonger (MN) pour couper les cotés du triangle
ABC qu'on appellera par exemple Q (sur AB) et R sur (AC).Tu joins Q et P ........A toi .