Bonsoir,
Je suis en terminale STL, j'ai déjà regarder plusieurs explication sur internet, mais je ne comprend toujours pas.
J'ai un exercice de mon cours que je ne comprend pas.
L'énoncer:
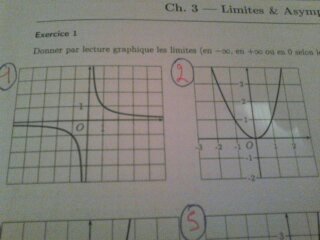
Donner par lecture graphique les limites( en -∞ ; en +∞ ou en 0 selon le cas ) de chacune de ces fonction.
je ne vois pas du tout comment je peut trouver la limite sans la fonction du graphique
Merci d'avance pour votre aide.
Les PJ ne sont pas encore affichée, mais regarde vers quoi tend f(x) quand x => +∞
Il peut s'agir soit d'une constante, soit de +-∞, soit la limite est indéterminée (dans le cas d'une fonction périodique par exemple)
Re : Lecture graphique de limite
Pour la lim f(x) quand x tend vers +∞ je trouve 0+, pour ça j'ai compris mais je ne comprend pas pourquoi lorsque x tend vers -∞ je trouve f(x)=+∞.
Ceci est dans la correction, il y a aussi écrit que
lim f(x) = -∞ lorsque x tend vers 0-
lim f (x)=+∞ lorsque x tend vers 0+
Que signifie "PJ" pour vous ?
Merci d'avoir répondu à la question
PJ = Pièce jointe.
Pour le 1)
x=>+∞ ; f(x) => 0+ c'est bon
x=>-∞ ; f(x) => 0- (regarde la courbe, on voit bien qu'elle se rapproche de y=0 par le dessous lorsque x diminue)
x=> 0+, on voit que y tend vers +∞ ; et inversement quand x=0-
Pour la 2)
Que x augmente ou diminue, tu vois que y augmente. On devine aisément qu'il s'agit de la fonction f(x)=x²
donc quelque soit x=>+-∞ ; f(x) => +∞
Tu as peut être du mal à comprendre la notion de "tendre vers".
Reprenons la 1ere fonction :
Si x=1 ; y=1
Si x=0,5 ; y = 2
Si x=0,25 ; y = 4
etc etc
Plus on va continuer vers x=0, plus y va devenir grand. On appelle cela la limite lorsque x tend vers 0+ (puisque l'on est du coté positif de x)
Là, en réfléchissant un peu, on devine qu'il s'agit de la fonction 1/x. On ne peut pas étudier le signe de 1/x en x=0. Il est égal à la fois à +∞ et -∞. On dit qu'il est indéterminé. L'astuce consiste donc à étudier le résultat quand x s'approche de 0, autrement dit 0+ et 0-.
Re : Lecture graphique de limite
Merci pour vos explication,elle m'ont beaucoup aider.
