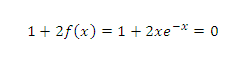Etude de fonctions exponentielles

[invite1f4580cf]

Bonjour bonjour.
Je suis en Terminale S et j'ai un DM de maths à rendre la semaine prochaine.
Il porte sur des études de fonctions, deux fonctions en fait
Pièce jointe 200006

J'ai réussi la première partie de l'exercice, mais je suis bloquée à la deuxième partie, celle de l'étude de la fonction g(x).

Dans les questions, on nous demande d'étudier le sens de variation de g, après avoir justifié la dérivabilité et avoir cherché la dérivée, qui est
Pièce jointe 200008

Pouuuurtant, je ne sais pas comment définir les extremums de g, pour faire le tableau des variations, car je suis bloquée à la partie où on égalise la dérivée à 0, j'ai d'abord trouvé x=1 mais pour la deuxième partie, je suis perdue face à l'équation


Merci d'avance pour votre aide...
-----

[jamo]

Bonjour
tu ne peux pas écrire l'énoncé car la pièce n'est pas encore validée .

[invite1f4580cf]

Ok ok.

Donc les deux fonctions:

f(x)=xe^(-x) ; g(x)=f(x)+[f(x) ]²

La dérivée de g(x):
g'(x) =f'(x)[1+2f(x) ] = (1e^-x-xe^-x)(1+2xe^-x)

Et je suis à l'égalisation de la dérivée à 0, pour trouver les extremums, j'ai d'abord trouvé x=1 pour 1e^-x-xe^-x=0

Mais pour 1+2xe^-x=0 je tombe et re-tombe sur x=-e^x/2 .. Et là, je ne sais plus...

[jamo]

tu sais que exp(x)>0 , que peux tu dire 1+2xe-x ?
sinon tu poses g(x)=1+2xexp(-x) , une petite étude et regarder si g s’annule.

[A voir en vidéo sur Futura]

[invite1f4580cf]

Hmmm effectivement...

Mais si on ne peut pas annuler 1+2xe^-x , est-ce que je dois considérer qu'un seul extremum donc?

Parce que avec cette inéquation, je ne suis pas vraiment sûr de trouver un autre extremum... Ou y a-t-il un autre moyen de définir l'autre, parce que d'après ma calculatrice graphique, il y a également un minimum atteint entre -1 et 0...