Décomposer des nombres premiers

[invite6462dd6d]

Inspiré par la manière dont les Mayas faisaient leur multiplications, une idée m'est venue pendant que je lisais un bouquin de statistique en buvant un 100% Arabica au Jdeed de Valbonne. J'écris cette idée sous la forme d'une conjecture car je ne sais pas la démontrer dans le cas général.

Conjecture de construction. Soient , et trois nombres entiers non nuls tels que :
- des éléments de est pair ;
- les n'ont aucun facteur commun ;
- pour un donné, si un élément de appartient à l'intervalle , alors les deux autre aussi.
Alors est un nombre premier.

Les nombres suivants vérifient la conjecture de construction :
1,2,3 ; 1,2,5 ; 1,2,7 ; 1,2,9 ;
2,3,5 ; 2,3,7 ;
3,4,5 ; 3,4,7 ;
4,5,7 ; 4,5,9 ;
5,6,7 ; 5,7,8 ;
7,8 9 ;
10,11,13 ; 10,11,17 ; 10,11,19 ; 10,13,17 ; 10,13,19 ; 10,17,19 ;
11,12,13 ; ...

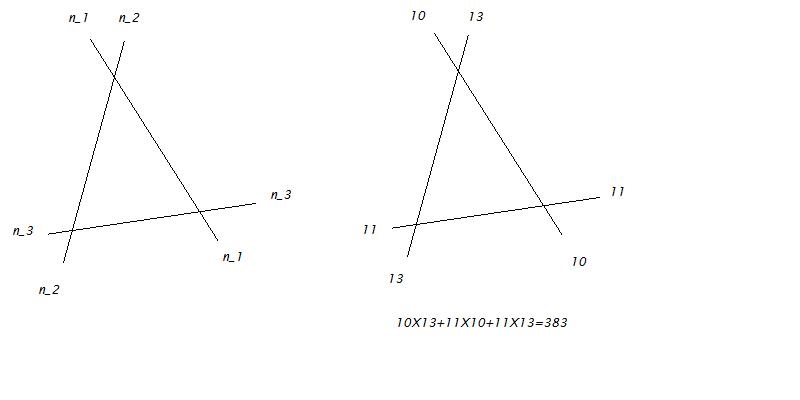
Pour le cas , on peut visualiser le nombre premier par un dessin. Réécrivons d'abord le produit comme .



Si on relâche un peu l'une ou plusieurs des trois contraintes de la conjoncture de construction, ce serait bien de montrer que tout nombre premier peut être décomposé comme le produit de trois nombres.

Conjecture de décomposition. Soient , et trois nombres entiers positifs dont au plus un est pair. N'importe quel nombre premier peut être décomposé comme le produit .
-----

[danyvio]

Les mots ont un sens :" tout nombre premier peut être décomposé comme le produit de trois nombres" est pour le moins paradoxal... Mais heureusement la suite indique implicitement : somme de trois produits ....

[invite6462dd6d]

Merci danyvio.

[invite6462dd6d]

J'invite les lecteurs à se rendre dans la catégorie mathématiques-supérieur où j'ai reproduit le message original et corrigé deux points, et car la charte du site interdit de poster plusieurs fois le même sujet.
Merci.

[A voir en vidéo sur Futura]