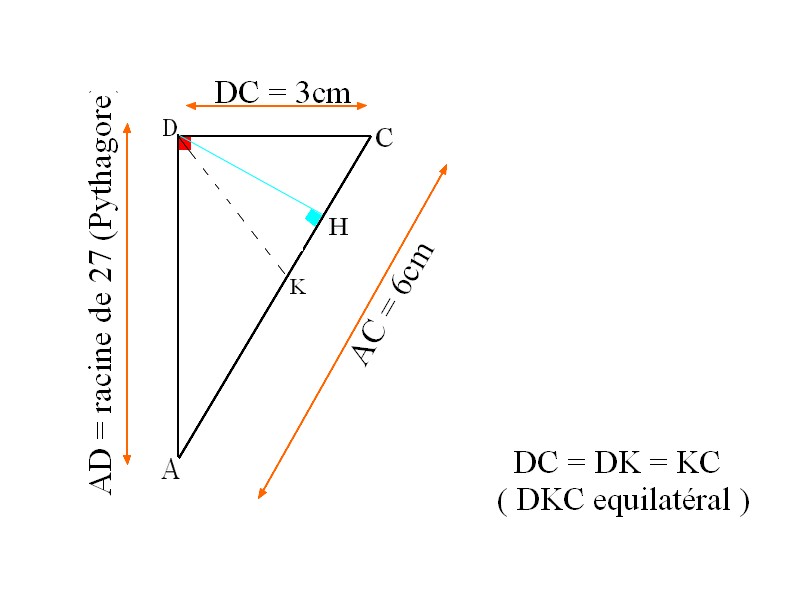
Bonjour à tous , j'ai récemment commencé le chapitre sur le produit scalaire, je suis en 1ere s et, pour les vacances, le professeur nous a donné des exercices pour nous entraîner. J'en ai réussi la majorité mais il y en a deux sur lesquels je bloque complètement ... C'est donc pour ça que j'ai besoin de votre aide. Dans l'attente d'une réponse, je vous souhaite une bonne journée.
Bonsoir.
Tu ne peux décemment pas dire que tu n'as rien fait, ce serait avouer que tu n'as pas appris tes leçons (cours sur le produit scalaire) et que tu attends qu'on fasse le travail à ta place (interdit par le réglement du forum).
Donc dis-nous ce que tu as fait et où tu bloques.
Cordialement.
Pour calculer un produit scalaire en général, il faut identifier les données: soit on connaît le projeté orthogonal, sooit un angle et deux longueurs, soit les trois côtés d'un triangle....
Pour le a, on a le projeté orthogonal de C sur (AB).....on sait aussi quepi/3
Pour le b, on peut se ramener à un calcul plus simple vect(KC).vect{CB}=-vect{CK}.vect{CB}
Pour le c, on peut trouver le projeté orthogonal de C et D sur (AB)...
Pour le d, on peut utiliser le projeté orthogonal de C ou bien
Quelques exemples de base si cela peut aider en pièce jointe.
J-F L (maths-s.fr)
Merci de vos réponses, il est évident que je n'attend pas que vous fassiez l'exercice à ma place mais j'aimerais des explications sur les points où je bloque.
En ce qui concerne le 36, avec l'aide fournie je trouve :
1)a) J est le projete orthogonal du point C sur (AB)
(vecAJ) et (vecAB) sont de même sens donc on a :
(vecAC) * (vecAB) = AJ*AB = 3*6 = 18
b) J est le projete orthogonal du point C sur (AB)
(vecJB) et (vecKC) sont de même sens donc on a :
(vecKC) * (vecCB) = KC*JB = ?*3 = ?
c) A est le projete orthogonal du point D sur (AB)
J est le projete orthogonal du point C sur (AB)
(vecAJ) et (vecBA) sont de sens inverse donc on a :
(vecDC) * (vecBA) = AJ*-BA = AJ*AB = 3*6 = 18
d) J est le projete orthogonal du point C sur (AB)
(vecAJ) et (vecAD) sont de même sens donc on a :
(vecAC) * (vecAD) = AJ*AD = 3*? = ?
2) Projeté othogonal du point D sur la droite (AC) = A
AH = 0 ?
En ce qui concerne le 90, j'ai compris la configuration (capture d’écran) mais pas le calcul à faire pour y arriver ...
J'espère que vous pourrez éclaircir les points où je bloque, merci d'avance
Tu ne connais pas la formule avec le cosinus ????
Aurais-tu oublié d'apprendre ton cours ???
Ah non je n'ai pas encore appris de formule avec le cosinus c'est peut être parce que je viens de commencer et que je n'ai pas encore abordé cette partie. Je vais donc faire des recherches sur internet en tout cas merci de l'aide fournie pour la méthode
etonnant puisse qu'on te propose d'utiliser les angles.
or, le produit scalaire fait ( par définition ) intervenir directement l'angle ( le cosinus ) entre les deux vecteurs !!!
Pour le 1) du 36 j'ai finalement réussi à tout trouver grâce au théorème de Pythagore mais maintenant j'ai un problème pour le 2) à moins que je n'ai pas compris, la figure se présente ainsi :
Mais comment calculer la longueur AH avec seulement 1 côté (AD) et un angle (AHD) ?
si V est un vecteur directeur de ta droite.
alors qu'en ai -t-il du produit scalaire de AH.V ?
ps , ton dessin est faux, d'après l'énoncé H est le projeté orthogonal de A sur la droite d ....
Merci de la réponse, mais je pense que nous avons eu un problème de compréhension car le dessin que j'ai effectué est pour le deuxièmement du 36 (On appelle H le projeté orthogonal du point D sur la droite (AC). Calculer la longueur AH." Autrement je ne voit pas mon erreur, l'angle bleu est bien rectangle donc la règle est respectée. Donc il reste la même question " Comment calculer la longueur AH avec seulement 1 côté (AD) et un angle (AHD) ? "
Bonjour,
Bon, les calculs peuvent ê tre faits sans les angles
Pour le 1 b, relire la première réponse et vect CK.vect CB ressemblera au a . (chercher le projeté orthogonal de B..........)
Pour le d, ABCD trapèzér rectangle en A, donc on peut trouver le projeté orthogonal de C sur ...........
2 penser que pourcalculer vectAC .vectAD on peut utiliser le projeté orthogonal de C sur (AD) où bien de D sur (AC).......
Pour le 90, tu as les cordonnées de A, de H(en fonction de a) et d'un vecteur directeur de d donc on peut calculer le produit scalaire de deux vecteurs orthogonaux....
Cordialement,
J F L maths-s.fr
ok,
piste suggérée
considère AJCD , rectangle qui vaut ( surface que tu connais ) 2 fois le rectangle ACD.
or, surface d'un rectangle hauteur*base/2
la hauteur vaut AH et la base AC .....
ps à lecar: c'est pas joli/joli de faire de l'auto promo d'un site sur FS ( mais je ne suis pas modérateur )
Si je suis le raisonnement ci-dessus :
AJCD a une aire de 18cm²
ACD a donc une aire de 18cm² / 2 = 9cm²
AH est la hauteur du triangle ADC
Aire d'un rectangle hauteur*base/2 = 9cm²
Base = AC Hauteur = AH
(6 * ?) / 2 = 9
9*2 = 18
18/6 = 3
? = 3
AH = 3
Est-ce juste ?
