Aide à montrer une inéquation

[physic]

bonjour,
Merci d'avance pour votre aide à la résolution au problème suivant

-----

[Duke Alchemist]

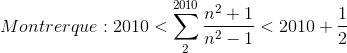
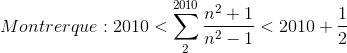
Bonjour.

Je te propose d'écrire le quotient sous une forme plus sympathique (genre en ajoutant et en retranchant "2"... Ajouter 0 quoi ).
Le 2010 apparaîtra très vite. Il ne restera plus qu'à montrer que le reste est compris entre 0 et 1/2.

Duke.

[physic]

bonjour,
merci de votre réponse. je vous prie de la détailler plus. merci encore.

[Seirios]

Et nous te prions de réfléchir un peu... Fais au moins l'effort de nous montrer que tu as réfléchi à la question.

[A voir en vidéo sur Futura]

[gg0]

Allez, un petit coup de pouce :

Pour n très grand, vaut quasiment 1. Donc
Valable aussi pour n'importe quelle valeur de n (sauf 1).

Bon travail !

[pallas]

un autre exemple (a+6)/(a-3)= (a-3+9)/(a-3)=1+9/(a-3)

[kermovan]

Bonjour.
J'ai essayé de faire ton exo et si tu veux le réussir il y a à mon avis certains points importants:
1) C'est très classique quand tu as un quotient dont on ne sait que faire de le transformer de la façon que t'ont indiqué Pallas et ggo. Ça n'en a peut-être pas l'air, mais ils te disent la même chose! (du moins je crois). J'en remet une couche: (n²+1)/(n²+3)=(n²+3-2)/(n²+3)=1-2/(n²+3). (évidemment je ne prends pas les bonnes valeurs, mais bon).
2) Une fois que tu as simplifié ton terme général (ce qui est dans ta somme) comme dit en 1, tu sommes tout ça. Encore une fois c'est classique: pour une somme compliqué, il est plus facile de modifier le terme général et après de mettre le symbole somme au dessus plutôt que d'attaquer directement la somme.
3) Par linéarité de la somme tu sais que la somme de 2 à 2010 de 1-2/(n²+3) c'est la somme de 2 à 2010 de 1 - la somme de 2 à 2010 de 2/n²+3 (toujours avec des chiffres fantaisistes, mais le principe reste le même).
4)la somme de 2 à 2010 de 1, ça devrait s'approcher de 2010 tu ne trouves pas?
5)il te reste à encadrer la somme de 2 à 2010 de 2/n²+3 entre 0 et 1/2.


Bon! Si je n'ai pas fait d'erreur (on n'est jamais sûr de rien) , ce que je te dis là dois bien te simplifier le travail.

P.S Au cas où tu n'as pas remarqué, je ne sais pas comment on met des équations (symbole somme etc) sur ce forum. Ce n'est pas compatible avec les pdf (il me bousille ma formule). Comment as tu fait? Merci

[ansset]

Bonjour.

Je te propose d'écrire le quotient sous une forme plus sympathique (genre en ajoutant et en retranchant "2"... Ajouter 0 quoi ).
Le 2010 apparaîtra très vite. Il ne restera plus qu'à montrer que le reste est compris entre 0 et 1/2.

Duke.

attention, il y a une subtilité car il n'y a que 2009 termes,
il convient de suivre la direction de ggo puis de montrer que le "reste" ( quand on a enlevé tous les "1" ) est inférieur à 3/2.

[ansset]

ps : la majoration des restes ne me semble pas triviale.
la convergence semble être justement de 3/2 ( ou très proche )

[gg0]

Oui, c'est ça.

Mais avec on obtient une forte simplification. Et même la valeur exacte de la somme.

On aimerait quand même avoir des nouvelles de Physic, qui ne montre aucun désir de faire cet exercice. S'il attend la réponse, c'est une idée de fainéant ! Et s'il l'a fait et ne le dit pas, c'est de l'impolitesse. J'espère que c'est seulement de l'indolence ...

Cordialement.

[Duke Alchemist]

Bonjour.

attention, il y a une subtilité car il n'y a que 2009 termes,
il convient de suivre la direction de ggo puis de montrer que le "reste" ( quand on a enlevé tous les "1" ) est inférieur à 3/2.

En effet, ansset !
physic.

Au fait, c'est gg0 et non ggo...

Cordialement,
Duke.

[Teddy-mension]

Bonjour à tous,

Juste :

Mais avec on obtient une forte simplification.

Et même plutôt .

Cordialement.

[ansset]

joli !
( je partage l'avis de gg0 sur le primo-posteur )
Cdt

[gg0]

Merci Teddy-Mension,

j'ai vu que c'était faux (c'est un calcul que j'ai fait 100 fois ), puis j'ai oublié la correction en rédigeant mon dernier paragraphe.

Cordialement.

[ansset]

100 fois ? je savais que se cachait un maso derrière le "gentil garçon organisateur"

[gg0]

Quand on fait faire des exercices sur les séries en post bac, on a souvent à utiliser des séries télescopiques. Sans compter les décompositions de fractions rationnelles, soit pour intégrer, soit pour les transformées de Laplace. Et évidemment, c'est le même calcul avec du n² ou du n ...

Je suis sûr que tu as résolu plus de 100 fois des équations du second degré ...

Cordialement.

[ansset]

oui, ma remarque était au second degré.
je pense que tu l'avais saisi.
j'ai fait énormément de simulation numérique, et donc aussi de résolution d'équations.
le plus dur étant de poser les bonnes plutôt que de les résoudre. ( travail d'ingé quoi ).