Aide DM TS conclusion

[invite6488a89f]

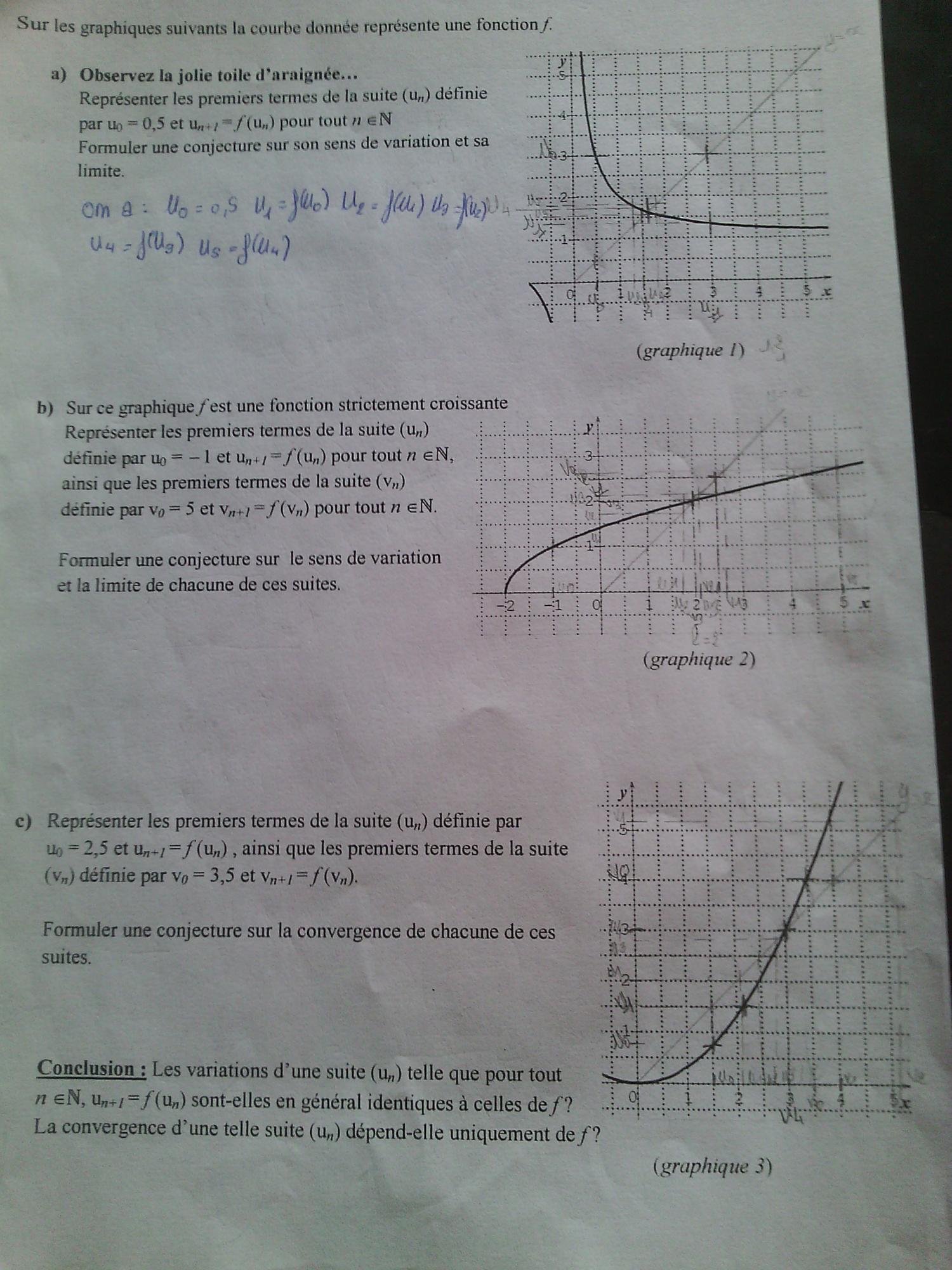
Bonjour a vous,

Alors voilà mon problème je doit conclure mon DM et on me demande :

Les variations d'une suite ( Un) telle que pour tout n E N, Un+1 = f(Un) sont-elles en général identiques à celles de f ?
La convergence d'une suite (un) dépend-elle uniquement de f ?

Sachant que j'ai 3 courbe , et que la première est décroissante ( fonction inverse les n positif ) et sa limite converge ( l = 1.2 )
la deuxième courbe est croissante = la limite de Un est divergente (+ l'infinie) et la limite de (Vn) est convergente ( l = 2 )
la troisième courbe est croissante = la limite de Un est convergente ( l= 3 ) et (VN) est divergente ( + l'infinie )
J'ai du pour ces 3 courbe formuler une conjecture sur le sens de variation et la limite ( ce que j'ai su faire )

Mais arriver a la conclusion je bloque complétement, j'ai commencé a formuler une repense qui est la suivante :

les variations d'une suite ( Un) telle que pour tout n E N , Un+1= f(Un) ne sont pas identique à celle de f car comme on le voit sur la première courbe , f est décroissante alors que les terme Un sont croissant et ils converge vers 1.2 .

Mais ma repense me parait fausse pourriez-vous m'éclairer !!
Cordialement
-----

[gg0]

Bonjour.

Soit tu t'es trompée auparavant, et c'est à toi de savoir si tu fais juste ou pas, soit tu conclus sur ce que tu as trouvé, et pourquoi serait-ce faux ?

Cordialement.

NB : "repense" est une conjugaison du verbe repenser; ce qui n'a rien à voir avec une réponse.

[invite6488a89f]

Voilà l'énoncé

[invite6488a89f]

Bonjour.

Soit tu t'es trompée auparavant, et c'est à toi de savoir si tu fais juste ou pas, soit tu conclus sur ce que tu as trouvé, et pourquoi serait-ce faux ?

Cordialement.

NB : "repense" est une conjugaison du verbe repenser; ce qui n'a rien à voir avec une réponse.

Je pense avoir fait une erreur dans le b) (la deuxième courbe) j'ai mis que Un était divergente mais elle est convergent et tend vers 2

[A voir en vidéo sur Futura]