Orthocentre
Bonsoir, j'ai un exo que j'ai pas pu faire !!
Voilà son énoncé:
soit abc un triangle on designe par C son cercle circonscrit de centre O et de rayon r soit g lecentre de gravité de ABC soit H telque OH=OA+OB+OC (en vecteur)
*Calculer AH.BC et BH.AC (produit scalaire)
*en déduire que H est l'orthocentre du ABC
merci de me donner des explications?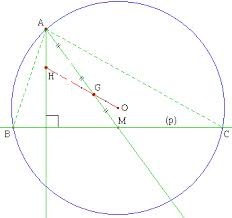
De la relation, tu peux utiliser Chasles pour introduire le point A (respectivement B) et obtenir une autre expression de
Noct comment j'ai pas compris tu peux m'expliquer un peu plus
Avec Chasles ,
et on a aussi
Donc
Pour le 2)
Une autre manière est de partir de OH=OA+OB+OC
Et de remplacer OA par OG+GA (Chasles), pareil pour OB et OC
Et se servir des deux relations suivantes:
Définition du centre de gravité: l'unique point G tel que GA+GB+GC=0
Relation d'Euler: OH=3OG
voir http://fr.m.wikipedia.org/wiki/Droite_d'Euler
Cordialement
NB: tout ça avec des petites flèches au dessus
c'est bon AH=OB+OC (en vecteur) => AH.BC=(OB+OC).BC=??
Est ce que je peux dire OB+OC=-BO+OC= -BC ?? donc AH.BC =-BC² ?? et meme chose por BH??
oui je trouve cette méthode mais on n'a pas déja vu EUler :'( déja le question suivant et de montrer que OH=3OG
Ceci est faux , c'est -BO-OC qui est égal à -BC.-BO+OC= -BC
Par contre en développant le produit scalaire , ça marche plutot bien. Et quelle est la nature du triangle OBC ?
OBC un triangle isocéle !! AH.BC= (OB+OC).BC ==> OB+OC= vecteur nul ?? =>AH.BC=0 c'est juste?
Alors tu as la réponse à la question suivanteEnvoyé par cleopatra1
merci Gandhi33 j'ai déja fais la 2eme question" de montrer que O H G sont alignés (par colinéarité) et je ne trouve pas le premier question merci en tout cas
Non car ça voudrait dire que O est le milieu de [BC]OB+OC= vecteur nul ??
Par contre OBC est isocèle donc il y a des angles égaux.
Développe le produit scalaire en utilisant les cosinus.
comme çà : BC.(OB+OC)= BC.OB+BC.OC (en vecteur)
=-BC.BO +CB.CO (en vecteur)
=-BC*BO*COS^B+ CB*CO* COS^c
=-BC*R*COS^B+ BC*R* COS^B=0 MEME CHOSE POUR BH ??
Oui , le raisonnement est le même pour l'autre produit scalaire
on a AH.BC=BH.AC=0 signifie AH et BC sont perpendiculaire et BH et AC sont perpendiculaire d'ou H est le orthocentre de ABC je peux dire çà ?
Je trouve ce raisonnement un peu trop rapide , je rajouterais une ligne , il faut montrer que tu as bien compris. AH et BC sont perpendiculaires et BH et AC sont perpendiculaires donc , [...] , donc H est l'orthocentre
comment? quel ligne??
Je voulais dire : Faire le lien avec la définition d'un orthocentre.
pas compris
Les trois hauteurs d'un triangle sont concourantes. Leur point d'intersection H, est nommé orthocentre du triangle. et alors ?
(AH) et (BH) sont des hauteurs de ABC, leur point d'intersection H est donc
l'orthocentre de ABC.
Ouic'est ça
