bonsoir,
j'ai besoins de votre aide je doit rendre ce devoir sur la fonction exponentiel (tout juste une nouvelle fonction, je ne suis pas top top je me perds souvent ), alors voila l'énoncer :
m est un paramètre réel et fm est la fonction définie sur R , par fm(x)= x+(m+1)e^-x
Cm est la courbe représentant fm dans un repère orthogonal. On a représenté certaines de ces courbes au dos de la feuille
1- montrer que pour tout réel m, les courbes Cm passent par un point fixe dont on précisera les coordonnées .
J'ai pas su répondre,( j'ai pas compris )
2.Dans cette question, m appartient à l'intervalle ]0;e[
a. Déterminer fm'(x) pour x E R
fm est définie et dérivable sur ]0;e] comme composé et produit de tel fonction
fm'(x)= (x)' + (mx+m)' * e^-x
= (mx+m)'*e^-x + (mx+m)*e^-x
=me^-x + e^-x * mx + e^-x * m
= e^-x (m+mx+m)
= e^-x ( mx+2m)
Je pense m'être tromper car qu'on je la re-dérive je ne troue pas fm''(x) = me^-x ( x-1)
b. Montrer que fm''(x) = me^-x ( x-1) pour x E R
c. Montrer que pour tout réel x E R, fm'(x) > 0 lorsque m e ]0;e]
d. En déduire le sens de variation de fm sur R
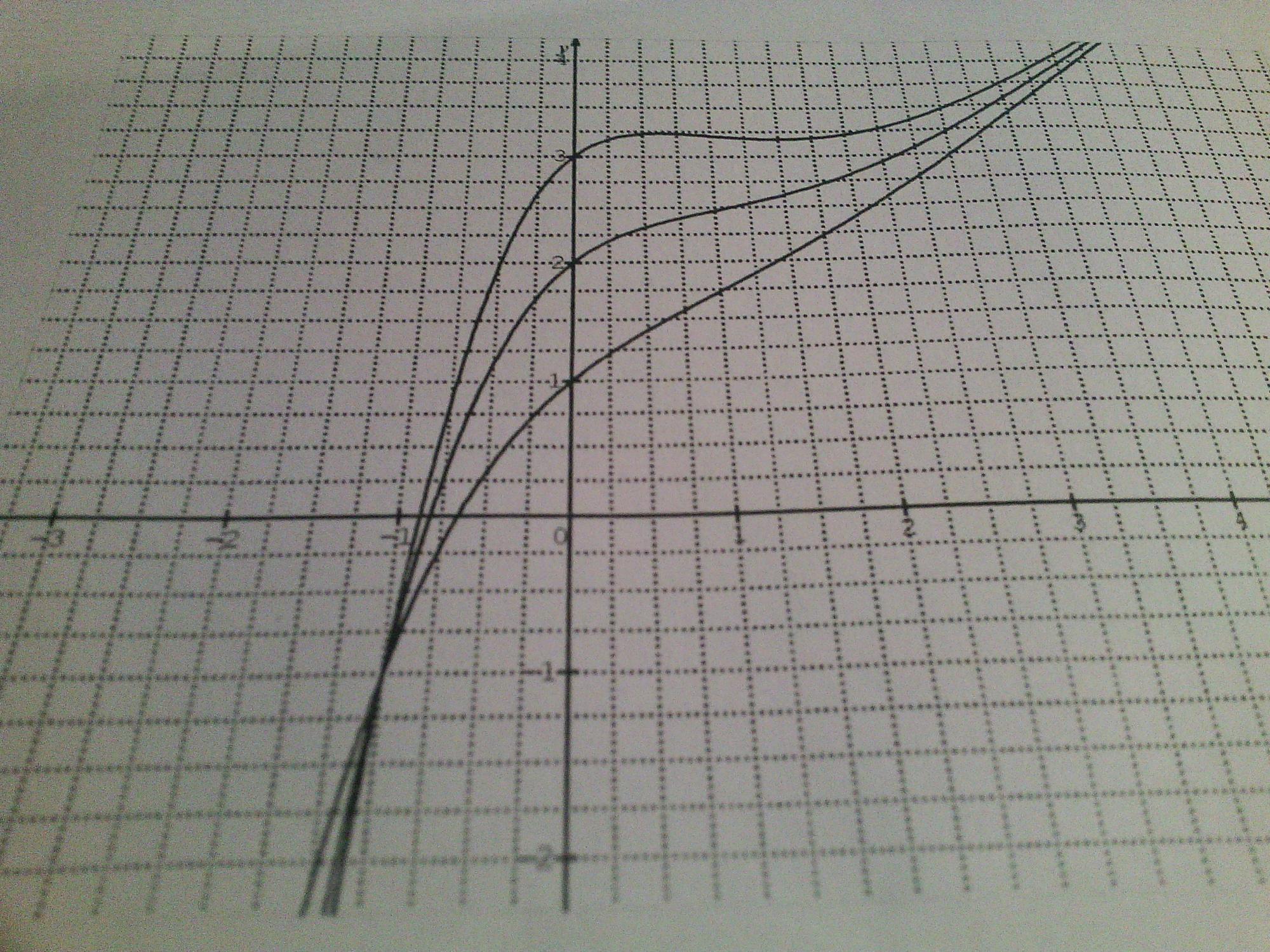
3- Sur le graphique au dos de la feuille, on a représenté la fonction fm pour trois valeurs de m diférentes
a- laquelles de ces courbes ne correspond pas à une valeur de m dans ]0;e], justifier
b- Déterminer graphiquement la valeur de m correspondant à la courbe E, justifier
Quelqu'un pourrait-il m'aider ? et prendre le temps de m'expliquer mes erreur ?
Cordialement
-----






 ne se coupent même pas !
ne se coupent même pas !